Теорема существования и единственности решения задачи Коши для ЛДУ го порядка
Пусть 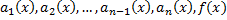 непрерывны на
непрерывны на 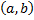 . Тогда для
. Тогда для 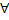 точки
точки 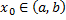 и
и 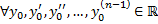
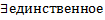 решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале
решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале 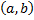 .
.
Рассмотрим левую часть ЛДУ (2.6.1) и (2.6.10) – дифференциальный оператор
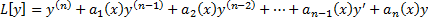 .
.
Покажем, что 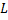 является линейным оператором, т.е.
является линейным оператором, т.е. 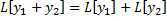 и
и 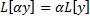 , где
, где 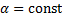 .
.
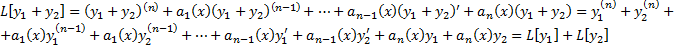 ,
,
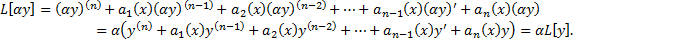
Таким образом, 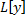 – линейный дифференциальный оператор.
– линейный дифференциальный оператор.
Операторная форма ЛДУ:
ЛНДУ:

ЛОДУ:

Линейные однородные ДУ (ЛОДУ) n-го порядка.
Теорема. Множество частных решений ЛОДУ n-го порядка 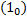 является линейным пространством относительно операций сложения функций и умножения на число.
является линейным пространством относительно операций сложения функций и умножения на число.
Док-во. Нужно доказать, что операции сложения частных решений и умножения частных решений на число не выводит из множества частных решений, т.е. сумма частных решений 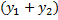 – также решение, произведение частного решения на число
– также решение, произведение частного решения на число 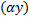 – также решение,
– также решение, 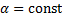 .
.
Пусть 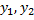 – решения, тогда
– решения, тогда 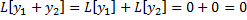 , т.е.
, т.е. 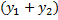 – решение,
– решение, 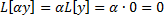 , т.е.
, т.е. 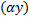 – также решение. Нулевым вектором в линейном пространстве решений ЛОДУ является функция
– также решение. Нулевым вектором в линейном пространстве решений ЛОДУ является функция 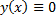 .
. 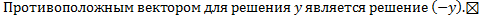
Итак, решения ЛОДУ n-го порядка 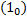 образуют линейное пространство.
образуют линейное пространство.
2.7. Линейная зависимость функций. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций и о вронскиане системы линейно независимых частных решений ЛОДУ.
Опр. Функции 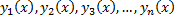 называются линейно зависимыми на
называются линейно зависимыми на 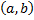 , если
, если 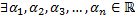 , не все равные
, не все равные 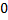 , такие, что
, такие, что 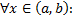
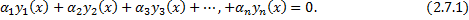
Опр. Если выполнение равенства ( 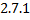 ) на всем интервале
) на всем интервале 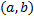 возможно только при
возможно только при 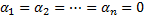 , то функции
, то функции 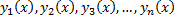 называются линейно независимыми на
называются линейно независимыми на 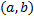 .
.
Критерий линейной зависимости:
Функции 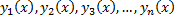 линейно зависимы на
линейно зависимы на 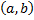
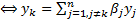 для некоторого k=1,….n (т.е. хотя бы одна из функций линейно выражается через остальные).
для некоторого k=1,….n (т.е. хотя бы одна из функций линейно выражается через остальные).
Пример.
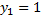
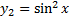
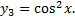
Т.к. 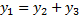 , то функции линейно зависимы на
, то функции линейно зависимы на 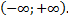
Пусть функции 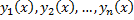
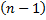 раз дифференцируемы на
раз дифференцируемы на 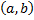 .
.
Опр. Определителем Вронского (вронскианом) системы функций 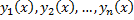 называется определитель
называется определитель
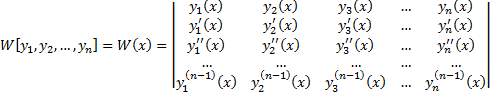 .
.
Теорема о вронскиане системы линейно зависимых функций
Пусть функции 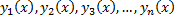 линейно зависимы на
линейно зависимы на 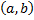 . Тогда
. Тогда 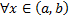 :
: 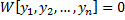
Док-во: по определению линейной зависимости функций 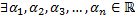 , не все равные
, не все равные 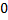 , такие, что
, такие, что 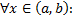
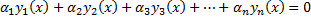 . Последовательно продифференцируем это равенство:
. Последовательно продифференцируем это равенство:
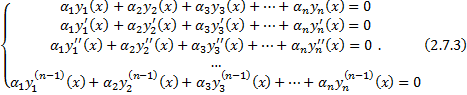
Зафиксируем 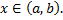
(2.7.2) – СЛАУ (однородных) относительно 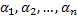 , которая имеет ненулевое решение, т.е. определитель системы равен
, которая имеет ненулевое решение, т.е. определитель системы равен 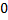 , т.е.
, т.е. 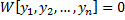 (
( 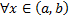 ).
). 
Замечание. Обратное неверно, т.е. если 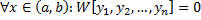 , то функции могут быть линейно независимы.
, то функции могут быть линейно независимы.
Пример.
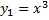 ,
,
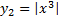 .
.
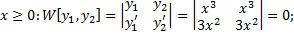
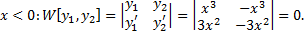
Т.е. 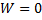 на
на 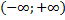 , но
, но 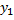 и
и 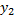 линейно независимы, т.к.
линейно независимы, т.к. 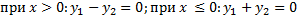 . Не существует
. Не существует 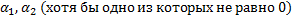 , таких, что
, таких, что 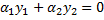 для всех
для всех 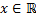 .
.








