Теорема Коши существования и единственности решения задачи Коши для ДУ 1-го порядка.
Пусть функция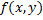 
и ее частная производная 
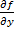непрерывны в области 
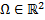. Тогда для 
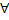точки 
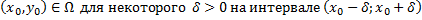существует и при том единственное решение задачи Коши.
Геометрический смысл: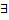 
единственная интегральная кривая, проходящая через т. 
.
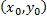Замечание. Решение определено только в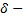 
окрестности т. 
.
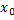Пример.
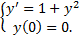
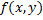и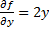 
непрерывны в области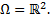 
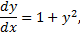
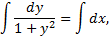
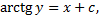
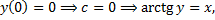
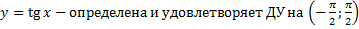, т.е. в окрестности точки 0. В любой большей окрестности 0 функция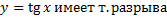 
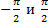и не удовлетворяет ДУ в этих точках.
Пример (неединственность в задаче Коши).
,
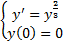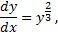
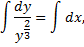
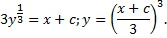
Из начального условия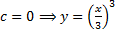 
.
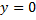– также решение данной задачи Коши.
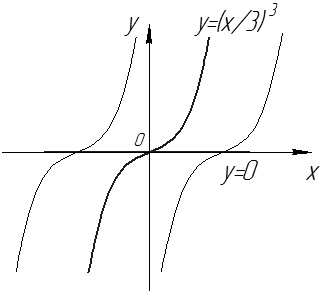
Рис. 31
Через точку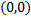 
проходит более одной интегральной кривой (см. рис. 31). Не выполняется условие непрерывности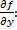 
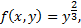
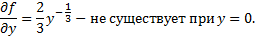
Опр. Общим решением ДУ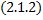 
называется семейство функций, зависящих от параметра 
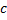, т.е. 
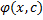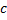, – произвольная постоянная, такое, что:
1. для фиксированного 
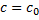функция 
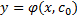является частным решением,
2. для 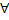т.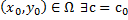 
такое, что частное решение 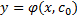удовлетворяет начальному условию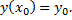 
Замечание. ДУ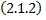 
можно записать в виде 
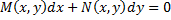(используя то, что 
.
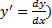Опр. Равенство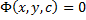 
, неявно задающее общее решение называется общим интегралом ДУ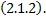 
2.2. Геометрическая интерпретация ДУ 1-го порядка. Поле направлений. Геометрическое решение ДУ 1-го порядка с помощью изоклин.
Пусть для ДУ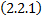 
выполняется условие существования и единственности, т.е. через любую точку 
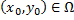проходит ровно одна интегральная кривая - график частного решения 
.
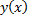Угловой коэффициент касательной к интегральной кривой в точке 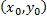равен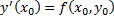 
. Таким образом, в каждой точке области 
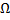ДУ (2.1.2) задает направление касательной к интегральной кривой, проходящей через эту точку 
В задано поле направлений (см. рис. 32).
Рис. 32
Опр. Изоклиной ДУ (2.1.2) называется кривая, во всех точках которой угловой коэффициент касательной к интегральной кривой, проходящей через заданную точку, одинаковый и равен заданному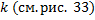 
.
Уравнение изоклины: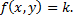 
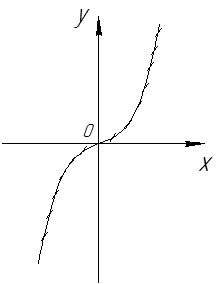
Рис. 33
Пример.
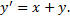
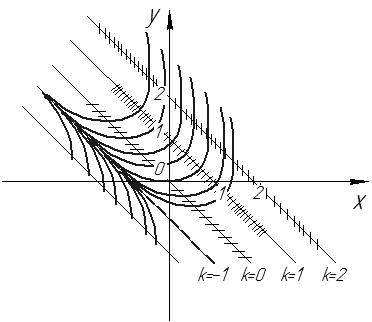
Рис. 34
Уравнение изоклин: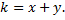 
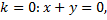
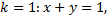
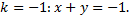
Прямая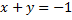 
является изоклиной 
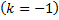и является интегральной кривой, т.к. 
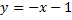– частное решение ДУ, т.е. является асимптотой для интегральных кривых (другие интегральные кривые приближаются к этой прямой, но не пересекают ее, т.к. через одну точку проходит только одна интегральная кривая.)
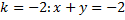
При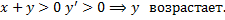 
При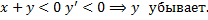 
Отсюда на прямой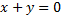 
находятся точки локального минимума решений ДУ.
.
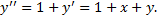
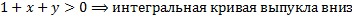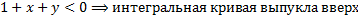(см. рис. 34).
2.3. Простейшие типы ДУ 1-го порядка (с разделяющимися переменными, однородные, линейные, Бернулли) и их решение.
1. ДУ с разделяющимися переменными
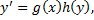
или
.
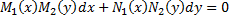Запишем ДУ в виде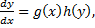 
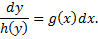
Проинтегрируем:
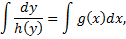
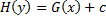– общий интеграл, 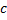– произвольная постоянная.
Замечание. Если уравнение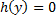 
имеет корни 
, то функции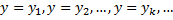 
являются частными решениями ДУ.
Пример.
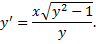
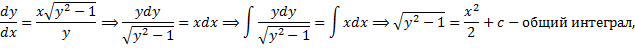
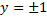– также решение ДУ.
2. Однородные ДУ
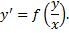
Замена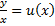 
, тогда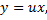 
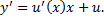
Тогда, подставляя в ДУ получим
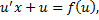
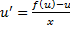– ДУ с разделяющимися переменными, находим 
.
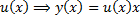Пример.
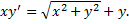
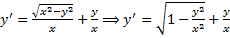(x>0).
Замена: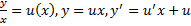 
. Подставим в ДУ:
,
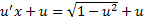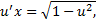
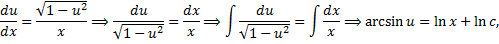
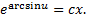
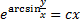– общий интеграл.
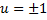– решение, т.е. 
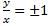, т.е. 
.
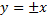3. Линейные ДУ 1-го порядка.
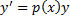– линейное однородное ДУ (ЛОДУ) 1-го порядка.
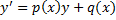– линейное неоднородное ДУ (ЛНДУ) 1-го порядка.
I. ЛОДУ 1-го порядка.
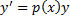– с разделяющимися переменными
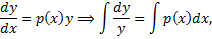
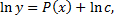
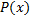– первообразная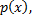 
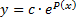
(р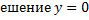 
получаем при 
).
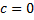II. ЛНДУ 1-го порядка.
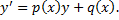
a. Решим соответствующее ЛОДУ: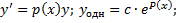 
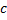– произвольная постоянная
b. Решение ЛНДУ ищем методом вариации постоянной, т.е. в виде
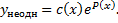
Тогда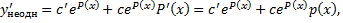 
Подставим в ЛНДУ: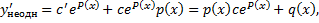 
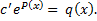
Находим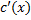 
; интегрируем, находим 
.
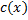Пример.
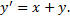
a. Соответствующее ЛОДУ: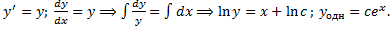 
b. Ищем решение ЛНДУ в виде 
Подставляем в ЛНДУ:
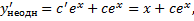
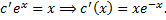
Проинтегрировав, получим
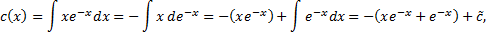
Подставим в (2.3.1):
= 
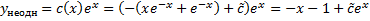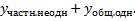
Замечание. ДУ
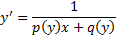
сводится к ЛНДУ относительно обратной функции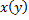 
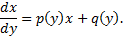
Решаем методом вариации произвольной постоянной:
.
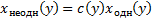4. Уравнения Бернулли
,
.
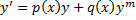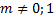Ищем решения в виде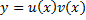 
. Подставим в ДУ:
,
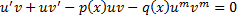Найдем функцию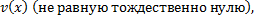 
такую, что
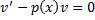– ДУ с разделяющимися переменными (ЛОДУ).
Используя (2.3.2), получим
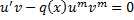
– ДУ с разделяющимися переменными. Найдем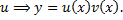 
Пример.
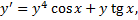
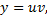
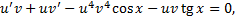
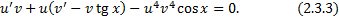
Найдем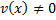 
из ДУ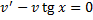 
.
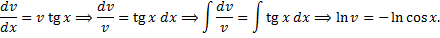
Подставим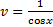 
в (2.3.3):
,
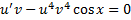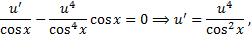
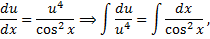
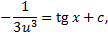
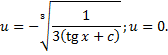
Тогда
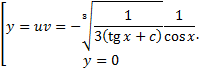
Замечание. ДУ
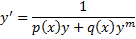
сводится к ДУ Бернулли относительно функции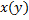 
:
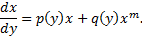
Решение ищем в виде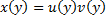 
Сведение ДУ Бернулли к ЛНДУ.
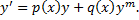
Разделим на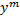 
(при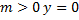 
– решение):
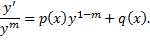
Пусть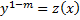 
, тогда 
,
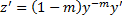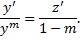
Подставим в ДУ:
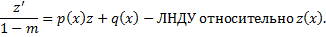
Пример.
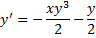
(ДУ Бернулли при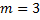 
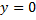; – решение).
Разделим на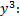 
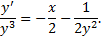
Замена
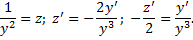
Подставим, получим
.
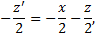
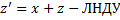Решая методом вариации постоянной, получим
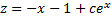, т.е.
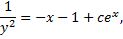
и
.
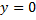2.4. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при n=2. Теорема существования и единственности решения задачи Коши. Краевая задача.
,
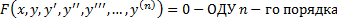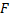– функция от 
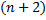переменных.
ДУ n-го порядка, разрешенное относительно старшей производной:
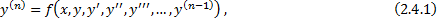
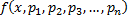определена в области 
.
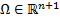Опр. Функция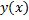 
называется частным решением ДУ (2.4.1)на интервале 
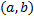, если при ее подстановке в (2.4.1) получается тождество на .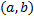