Объемы тел вращения.
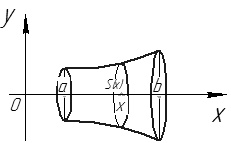
Рис. 26
Фигура, ограниченная линиями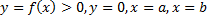 
, вращается вокруг оси 
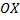(см. рис. 26).
Найдем объем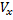 
тела вращения. Зафиксируем 
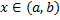. Сечение тела плоскостью 
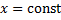– круг радиуса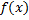 
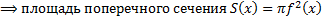. Тогда
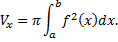
Ту же фигуру вращаем вокруг оси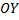 
(см. рис. 27).
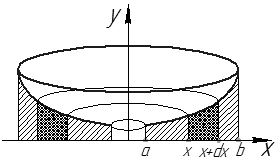
Рис. 27
Рассмотрим малый отрезок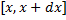 
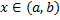, где . При вращении соответствующей части фигуры получаем тело объема 
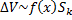, где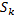 
– площадь кольца радиусов 
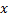и 
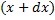соответственно:
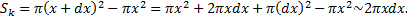
Тогда
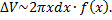
Суммируя по тонким "слоям", получим
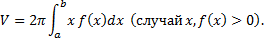
Общий случай:
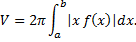
Таким образом получаем для вращения фигуры, ограниченной линиями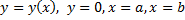 
, имеем
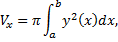
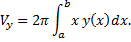
При вращении фигуры, ограниченной линиями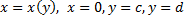 
(см. рис. 28).
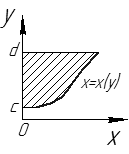
Рис. 28
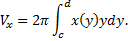
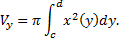
1.10. Вычисление длин дуг кривых и площадей поверхностей вращения
Длина дуги кривой.
Пусть дуга 
задана параметрическими уравнениями:
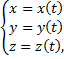
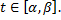
Функции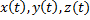 
имеют на 
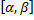непрерывные производные.
, 
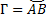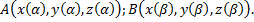
Рассмотрим переменную точку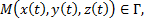 
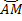– переменная дуга длиной 
.
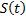Дифференциал дуги
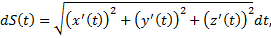
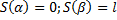– длина всей дуги.
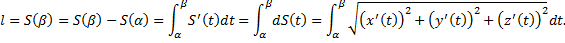
Случай плоской кривой:
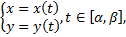
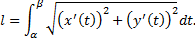
Случай графика функции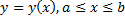 
:
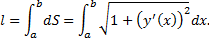
Случай кривой, заданной в полярных координатах:
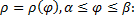
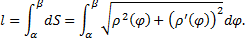
Площадь поверхности вращения.
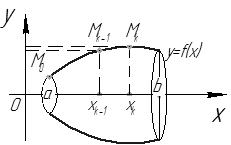
Рис. 29
Рассмотрим функцию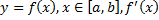 
– непрерывна на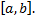 
Пусть – дуга графика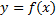 
– вращается вокруг оси 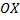. Рассмотрим ломаную 
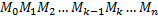, вписанную в дугу , где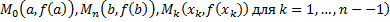 
(см. рис. 29).
При вращении вокруг 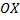звена ломаной 
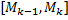получим боковую поверхность усеченного конуса.
Опр. Площадью поверхности вращения называется предел сумм площадей боковых поверхностей усеченных конусов, полученных при вращении вписанной ломаной, при стремлении к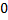 
максимальной длины звена ломаной.
Площадь боковой поверхности усеченного конуса с радиусами основани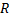й 
и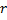 
и образующей 
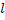равна
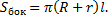
В данном случае
, 
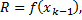
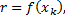
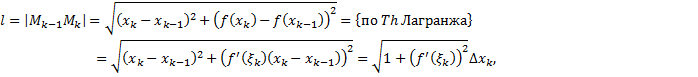
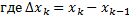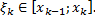
Тогда площадь боковой поверхности усеченного конуса , полученной при вращении звена ломаной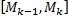 
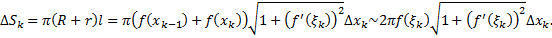
Отсюда площадь поверхности вращения
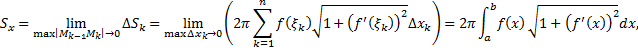
или
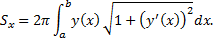
(при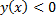 
надо брать 
).
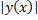Случай кривой, заданной параметрическими уравнениями:
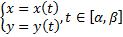
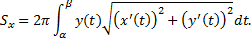
Случай кривой, заданной в полярных координатах:
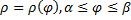
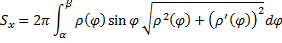
Аналогично при вращении вокруг оси :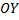
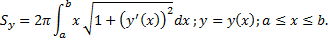
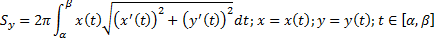
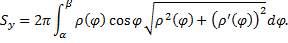
Случай произвольной оси вращения:
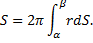
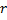– расстояние от переменной точки кривой до оси вращения; 
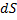– дифференциал дуги.
2. Обыкновенные дифференциальные уравнения.
2.1. Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ.
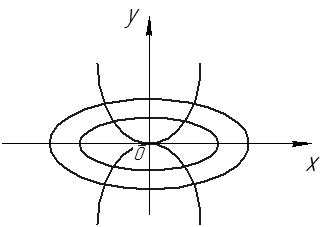
Рис. 30
Рассмотрим на плоскости семейство эллипсов
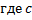– произвольная положительная постоянная (см. рис. 30).
Найдем семейство кривых, ортогональных семейству эллипсов.
1. Составим дифференциальное уравнение (ДУ) семейства эллипсов.
Продифференцируем уравнение (2.1.1), считая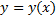 
:
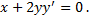
Отсюда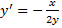 
- ДУ семейства эллипсов. Тогда 
= 
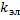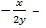
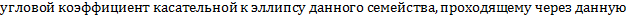
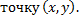
2. Составим ДУ ортогонального семейства. В т.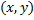 
угловой коэффициент касательной должен быть равен 
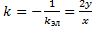, т.е. ДУ ортогонального семейства:
.
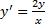3. Найдем уравнение ортогонального семейства:
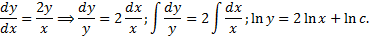
Получаем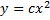 
– семейство парабол.
Обыкновенное ДУ 1-го порядка -
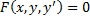, где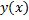 
– неизвестная функция; 
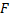– функция 3-х переменных.
ДУ 1-го порядка, разрешенные относительно производной:
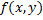– определена в области 
.
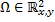Опр. Частным решением ДУ (2.1.2) называется функция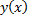 
, определенная на 
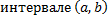, при подстановке которой в ДУ (2.1.2) оно обращается в тождество на 
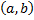, т.е. 
.
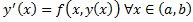Пример.
.
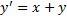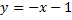– частное решение, т.к. 
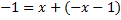– тождество;
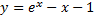– также частное решение, т.к. 
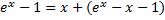– тождество.
Опр. График частного решения 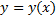ДУ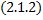 
называется интегральной кривой ДУ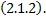 
Опр. Равенство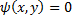 
, неявно задающее решение ДУ 
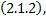называется частным интегралом ДУ .
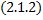Задача Коши для ДУ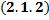 
: найти частные решения ДУ 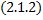, удовлетворяющие начальному условию 
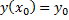, где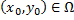 
,
т.е. задача Коши может быть записана следующими образом:
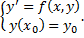
Геометрический смысл: найти интегральную кривую ДУ 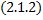, проходящую через т. 
.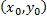