Вычисление несобственного интеграла 2-го рода.
Случай функции с особой точкой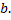 
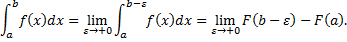
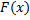– первообразная для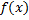 
Таким образом,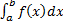 
сходится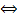 
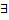конечный предел первообразной 
.
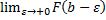Примеры.
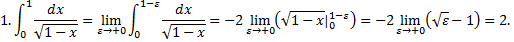
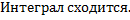
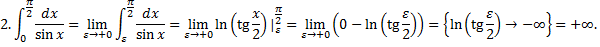
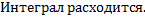
Рассмотрим интегралы
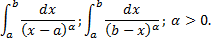
Рассмотрим случай интеграла с особой точкой в левом конце отрезка:
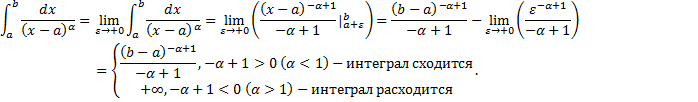
Случай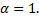 
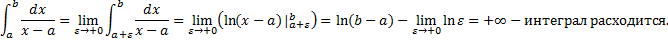
Аналогично рассматривается интеграл с особой точкой в правом конце отрезка. Таким образом
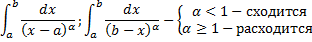
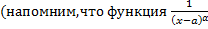имеет при 
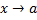порядок роста 
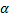относительно 
).
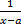Исследование несобственных интегралов 2-го рода на сходимость.
Признаки сходимости:
1. Признак сравнения:
пусть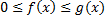 
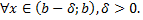
a. Если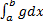 
сходится, то 
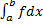также сходится.
b. Если 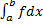расходится, то 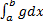также расходится.
2. Предельный признак сравнения.
Пусть для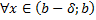 
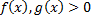и 
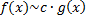при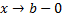 
, т.е. 
.
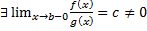Тогда 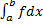и 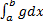оба сходятся или оба расходятся.
3. Если сходится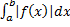 
, то сходится и .
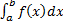Примеры.
1.
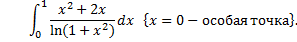
При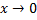 
,
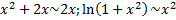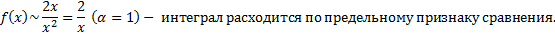
2.
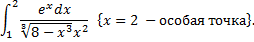
При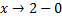 
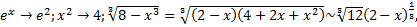
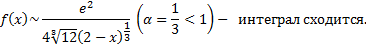
Замечание: если 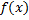непрерывна на 
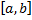кроме точк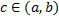и 
и 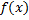не ограничена в окрестности точки 
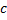, тогда
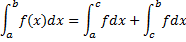
(для первого и второго интегралов в правой части особой точкой является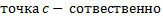 
правый или левый конец отрезка).
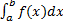сходится 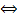сходятся оба интеграла 
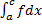и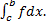 
Пример.
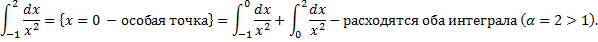
Примеры несобственных интегралов с несколькими особыми точками
1. 
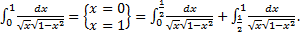
Исходный интеграл сходится, если сходятся оба интеграла в правой части:
a.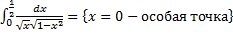 
.
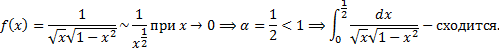
b.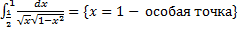 
.
.
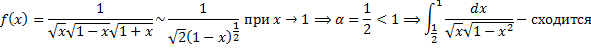
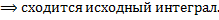
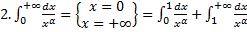(несобственный интеграл 2-го рода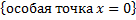 
+ несобственный интеграл 1-го рода 
).
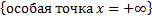a.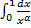 
– сходится при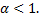 
b.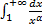 
– сходится при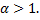 
Значит,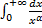 
расходится для любого .
.
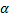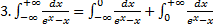a.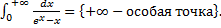 
При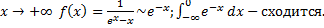 
b.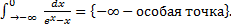 
При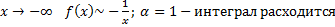 
.
Таким образом исходный интеграл расходится.
Абсолютная и условная сходимость несобственных интегралов.
Рассмотрим несобственный интеграл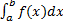 
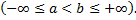
Опр. Несобственный интеграл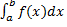 
называется абсолютно сходящимся, если сходится интеграл 
.
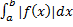Опр. Несобственный интеграл 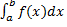называется условно сходящимся, если он сходится, но интеграл 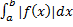расходится.
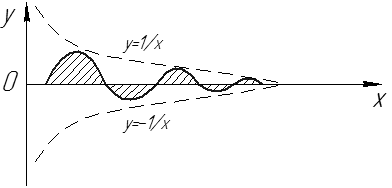
Пример.
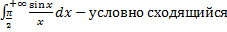(без доказательства, см. рис. 17).
| Рис. 17 |
1.8. Вычисление площадей плоских фигур в декартовых и полярных координатах.
| Рис. 18 |
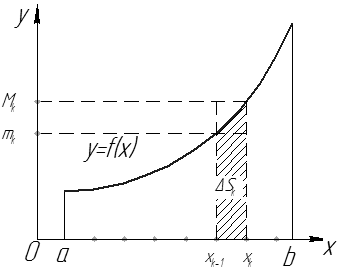Вычисление площадей плоских фигур в декартовых координатах
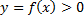непрерывна на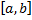
Найдем площадь фигуры, ограниченной линиями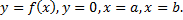 
Пусть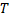 
– разбиение отрезка 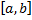на элементарные отрезки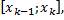 
; 
; 
.
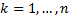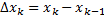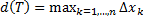Рассмотрим площадь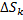 
части фигуры, удовлетворяющей условию 
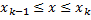. Пусть 
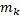и 
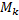– соответственно наименьшее и наибольшее значения функции 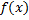на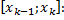 
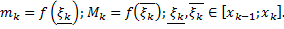
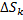заключена между площадями прямоугольников с высотой 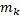и 
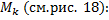
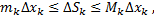
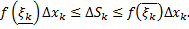
Сложим по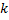 
от 
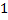до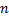 
:
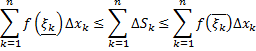
Т.е.
где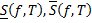 
– интегральные суммы, соответствующие разбиению 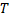и выбору точек 
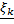и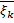 
соответственно (нижняя и верхняя интегральные суммы Дарбу); при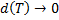 
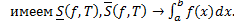
Из (1.9.1) получаем: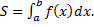 
Замечания:
1. 
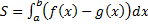(см. рис. 19.)
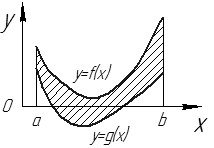
Рис. 19
2. 
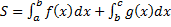(см. рис. 20).
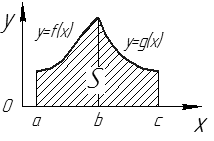
Рис. 20
3. 
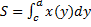(см. рис. 21).
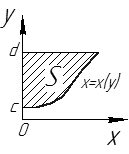
Рис. 21
Вычисление площадей плоских фигур в полярных координатах.
Рассмотрим кривую,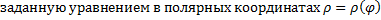 
, где функция 
непрерывна на 
.
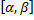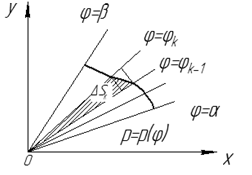
Рис. 22
Найдем площадь фигуры, ограниченной линиями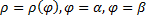 
. Пусть 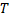– разбиение :
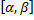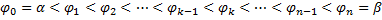
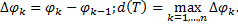
Рассмотрим площадь 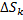части фигуры, удовлетворяющей условию 
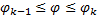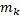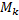(см. рис. 22). Пусть и – соответственно наименьшее и наибольшее значения функции 
:
.
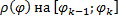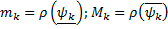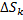заключена между площадями круговых секторов радиусов 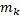и :
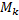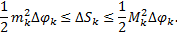
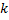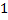Сложим по от до :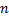
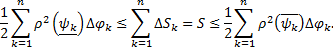
Т.е.
где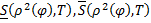 
– интегральные суммы функции 
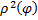, соответствующие разбиению 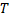и выбору точек 
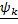и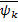 
соответственно (нижняя и верхняя интегральные суммы).
При 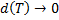из (1.9.2) получаем: 
.
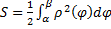Замечания:
1. 
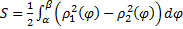(см. рис. 23).
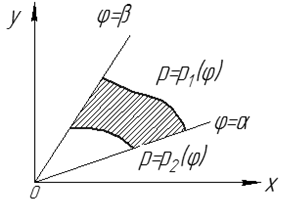
Рис. 23
2. 
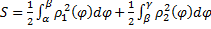(см. рис. 24).
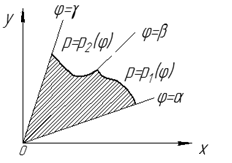
Рис. 24
1.9. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения.
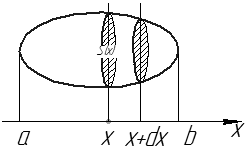
Рис. 25
Рассмотрим в пространстве тело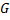 
, каждая точка 
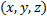которого удовлетворяет неравенству 
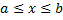. Пусть площадь сечения 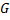плоскостью 
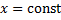равна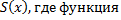 
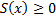непрерывна на 
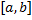. Найдем объем 
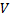тела 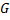. Зафиксируем 
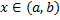. Рассмотрим малое 
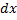. Рассмотрим часть (слой) тела 
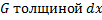, соответствующий отрезку 
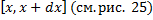. Объем этой малой части 
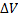приблизительно (c точностью до бесконечно малых выше первого порядка относительно 
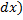равен объему цилиндра с площадью основания 
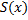и высотой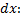 
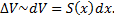
Суммируя по всем таким тонким слоям, получаем
