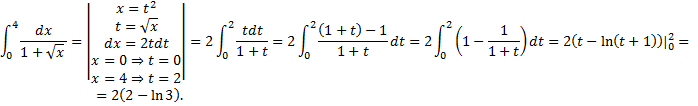Определенный интеграл как предел интегральных сумм.
Пусть функция 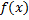 определена на
определена на 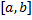 .
.
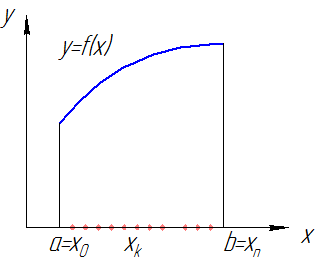
Опр. Разбиением 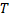 отрезка
отрезка 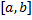 называется совокупность точек
называется совокупность точек 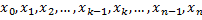 , где
, где 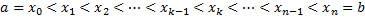 .
.
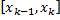 – элементарный отрезок (
– элементарный отрезок ( 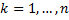 ),
),
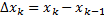 ,
, 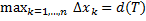 – диаметр разбиения
– диаметр разбиения 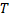 .
.
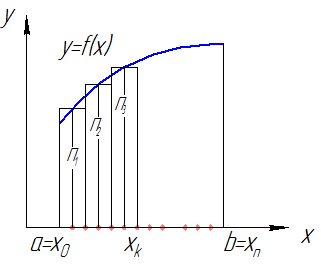
Выберем произвольные точки 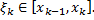
| Рис. 1 |
 Опр. Интегральной суммой функции
Опр. Интегральной суммой функции 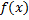 , соответствующей разбиению
, соответствующей разбиению 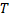 отрезка
отрезка  и выбору точек
и выбору точек 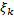 (
( 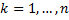 ) называется величина
) называется величина 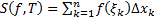 (см. рис. 1).
(см. рис. 1).
Опр. Определенным интегралом функции 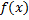 на отрезке
на отрезке  называется конечный предел при
называется конечный предел при 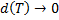 интегральных сумм
интегральных сумм 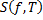 , если он существует и не зависит от способа разбиения отрезка и выбора точек
, если он существует и не зависит от способа разбиения отрезка и выбора точек 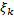 .
.
Обозн.: 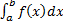 , т.е.
, т.е.
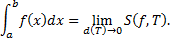
Тогда масса неоднородного стержня: 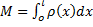 ; координата точки:
; координата точки: 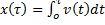 .
.
Опр. Если для функции 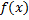 существует
существует 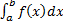 , то функция называется интегрируемой (по Риману) на
, то функция называется интегрируемой (по Риману) на  .
.
Теорема (необходимое условие интегрируемости.)
Пусть функция 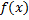 интегрируема на
интегрируема на  , тогда
, тогда 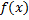 ограничена на
ограничена на 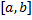 .
.
Теорема (достаточное условие интегрируемости 1).
Непрерывная на  функция
функция 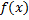 является интегрируемой на
является интегрируемой на 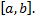
Теорема (достаточное условие интегрируемости 2).
Пусть 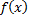 непрерывна на
непрерывна на  кроме конечного числа точек разрыва первого рода
кроме конечного числа точек разрыва первого рода 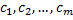 , тогда
, тогда 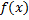 является интегрируемой на
является интегрируемой на 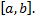
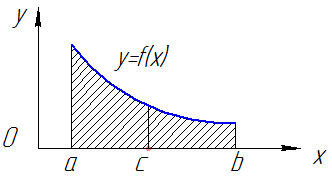
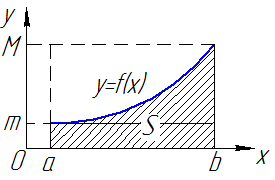
Геометрическая интерпретация определенного интеграла. 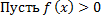 , непрерывна на
, непрерывна на 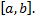
| Рис. 2 |
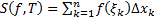 .
.
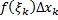 – площадь прямоугольника
– площадь прямоугольника 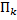 со сторонами
со сторонами 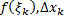 (см. рис. 2).
(см. рис. 2).
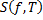 – площадь ступенчатой фигуры
– площадь ступенчатой фигуры
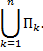
При 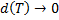 получим площадь криволинейной трапеции, ограниченной графиком функции
получим площадь криволинейной трапеции, ограниченной графиком функции 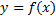 сверху, осью
сверху, осью 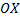 снизу и прямыми
снизу и прямыми 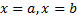 .
.
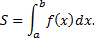
Свойства определенного интеграла
1. Линейность
Пусть функции 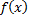 и
и 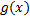 интегрируемы на
интегрируемы на 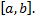 Тогда
Тогда
a. функция 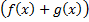 интегрируема на
интегрируема на  и
и 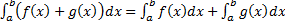
b. функция 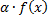 (
( 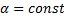 ) интегрируема на
) интегрируема на  и
и 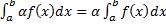
Док-во:
a. составим интегральную сумму для функции 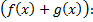
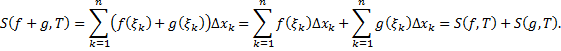
Тогда
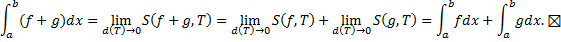
b. Аналогично
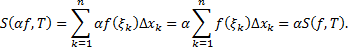
Тогда
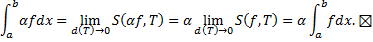
2. Аддитивность (см. рис. 3).
Пусть функция 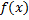 интегрируема на
интегрируема на  , точка
, точка 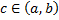 , тогда
, тогда
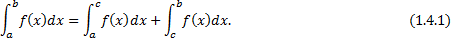
Док-во:
Рассмотрим разбиение 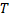 отрезка
отрезка 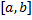 такое, что
такое, что 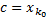 для некоторого
для некоторого 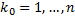 . Ему соответствуют разбиения отрезков
. Ему соответствуют разбиения отрезков 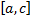 и
и 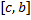 , соответственно,
, соответственно, 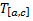 и
и 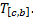
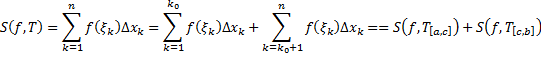
| Рис. 3 |
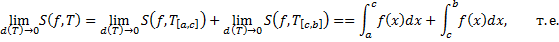
Т.е.
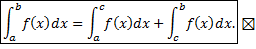
Замечание. Если 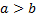 , то по определению
, то по определению 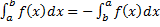 ,
,
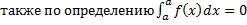 . Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек
. Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек 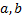 ,
, 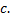
Теорема (об оценке определенного интеграла)
Пусть 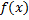 интегрируема на
интегрируема на  ,
, 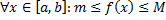 .
.
Тогда
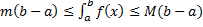 .
.
Док-во: 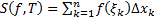 . Т.к.
. Т.к. 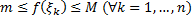 , то
, то 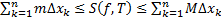 ,
, 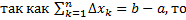
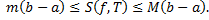
При  получим
получим 

| Рис. 4 |
 Геометрическая интерпретация:
Геометрическая интерпретация:
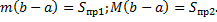
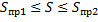 (площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4).
(площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4).
Следстви e (интегрирование неравенства).
Пусть 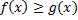 на
на  , тогда
, тогда 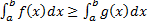 .
.
Док-во: рассмотрим функцию 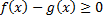 на
на  . Возьмем
. Возьмем 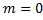 . По теореме об оценке
. По теореме об оценке
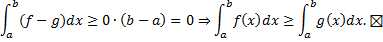
Пример.
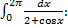 т.к.
т.к. 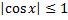 , то
, то 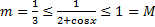 . По теореме об оценке
. По теореме об оценке 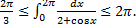
Теорема (о среднем значении для определенного интеграла).
Пусть 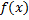 непрерывна на
непрерывна на  . Тогда
. Тогда 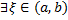 такая, что
такая, что 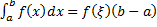 .
.
Док-во: т.к. 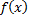 непрерывна на
непрерывна на  , то она достигает на
, то она достигает на  своего наибольшего и наименьшего значений
своего наибольшего и наименьшего значений 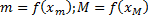 ,
, 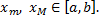 По теореме об оценке
По теореме об оценке 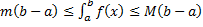 , (равенство возможно только для
, (равенство возможно только для  т.е. для непрерывных функций, отличных от константы
т.е. для непрерывных функций, отличных от константы 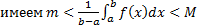 . По теореме о промежуточном значении непрерывной функции:
. По теореме о промежуточном значении непрерывной функции: 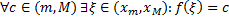 . Возьмем
. Возьмем 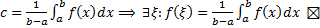 .
.
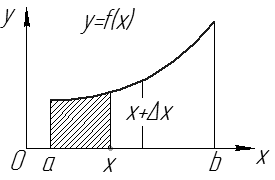
1.5. Определенный интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом. Формула Ньютона-Лейбница.
Пусть 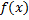 интегрируема на
интегрируема на  . Зафиксируем
. Зафиксируем 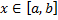 . Рассмотрим определенный интеграл по
. Рассмотрим определенный интеграл по 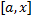 :
:
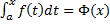 – определенный интеграл с переменным верхним пределом (см. рис. 5).
– определенный интеграл с переменным верхним пределом (см. рис. 5).
Теорема (о производной интеграла с переменным верхним пределом).
Пусть 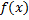 непрерывна на
непрерывна на  . Тогда
. Тогда 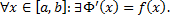
| Рис. 5 |
 Док-во:
Док-во: 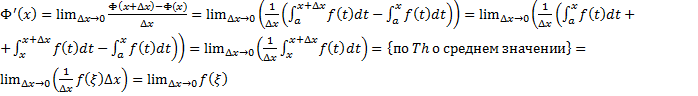 , где
, где 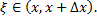
При 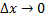
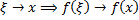 , (т.к.
, (т.к. 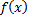 – непрерывная функция) т.е.
– непрерывная функция) т.е. 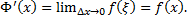

Следствие: если 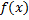 непрерывна на
непрерывна на  , то на
, то на  существует ее первообразная
существует ее первообразная 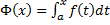 . Любая первообразная имеет вид
. Любая первообразная имеет вид 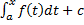 .
.
Пример.
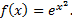
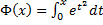 – первообразная для
– первообразная для 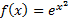 (не выражается через элементарные функции, интеграл – неберущийся).
(не выражается через элементарные функции, интеграл – неберущийся).
Формула Ньютона-Лейбница.
Пусть 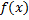 непрерывна на
непрерывна на  ,
, 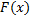 – ее первообразная. Тогда
– ее первообразная. Тогда 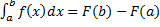 .
.
Док-во: пусть 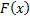 – произвольная первообразная. Рассмотрим
– произвольная первообразная. Рассмотрим 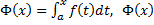 – также первообразная. Тогда
– также первообразная. Тогда 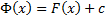 . Возьмем
. Возьмем 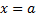 . Т.к.
. Т.к. 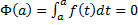 , то
, то 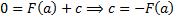 , т.е.
, т.е. 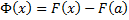 . При
. При 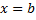 :
: 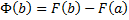 или
или 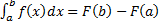 :
:
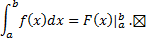
Пример.
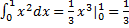 .
.
1.6. Вычисление определенного интеграла подстановкой и по частям. Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат, интегрирование периодических функций.
Пусть 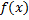 непрерывна на
непрерывна на  , функция
, функция 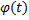 имеет непрерывную производную на
имеет непрерывную производную на 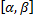 , причем
, причем 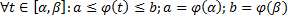 . Тогда
. Тогда 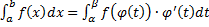 .
.
Док-во: пусть 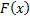 –первообразная для
–первообразная для 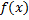 на
на  , т.е.
, т.е. 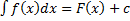 . Тогда по формуле Ньютона-Лейбница:
. Тогда по формуле Ньютона-Лейбница: 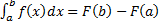 . Функция
. Функция 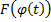 – первообразная для
– первообразная для 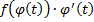 , по формуле Ньютона-Лейбница:
, по формуле Ньютона-Лейбница: 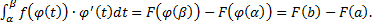
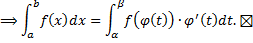
Пример.