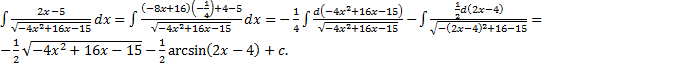Теорема 1 (об арифметических свойствах первообразной).
Московский государственный технический университет
имени Н.Э. Баумана
Факультет фундаментальные науки»
Кафедра «Высшая математика»
А.В. Неклюдов
Интегралы и
диффереренциальные уравнения
Электронное учебное издание
Лекции по курсу
Москва
(С)2013 МГТУ им. Н.Э. Баумана
УДК: 517.3
Рецензент:
Неклюдов А.В., Интегралы и дифференциальные уравнения. Лекции по курсу" - М., МГТУ им. Н.Э. Баумана, илл. 42.
Изложены основы интегрального исчисления функций одной переменной и теории обыкновенных дифференциальных уравнений. Большая часть теории излагается с подробными доказательствами, пояснениями и примерами.
Для студентов, изучающих и применяющих математический анализ и обыкновенные дифференциальные уравнения.
Рекомендовано Учебно-методической комиссией факультета "Фундаментальные науки" МГТУ им. Н.Э. Баумана.
Оглавление
1. Интегральное исчисление функций одного переменного. 5
1.1. Первообразная. Теоремы о первообразных. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов. 5
1.2. Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций. 6
1.3. Интегрирование рациональных дробей. Разложение правильной рациональной дроби в сумму простейших. Интегрирование простейших дробей. Интегрирование неправильных рациональных дробей. 11
1.4. Определенный интеграл, его механический и геометрический смысл, теорема существования. Линейность и аддитивность определенного интеграла. 14
1.5. Определенный интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом. Формула Ньютона-Лейбница. 17
1.6. Вычисление определенного интеграла подстановкой и по частям. Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат, интегрирование периодических функций. 18
1.7. Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Абсолютная и условная сходимость несобственных интегралов. 20
1.8. Вычисление площадей плоских фигур в декартовых и полярных координатах. 26
1.9. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. 29
1.10. Вычисление длин дуг кривых и площадей поверхностей вращения. 31
2. Обыкновенные дифференциальные уравнения. 33
2.1.Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ. 34
2.2. Геометрическая интерпретация ДУ 1-го порядка. Поле направлений. Геометрическое решение ДУ 1-го порядка с помощью изоклин. 36
2.3. Простейшие типы ДУ 1-го порядка (с разделяющимися переменными, однородные, линейные, Бернулли) и их решение. 38
2.4. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при n=2. Теорема существования и единственности решения задачи Коши. Краевая задача. 42
2.5. Понижение порядка некоторых типов ДУ высших порядков. 43
2.6. Линейные ДУ (ЛДУ) n-го порядка: однородные (ЛОДУ) и неоднородные (ЛНДУ). Теорема существования и единственности решения. Линейный дифференциальный оператор. Свойства линейного дифференциального оператора и линейность пространства решений ЛОДУ. 44
2.7. Линейная зависимость функций. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций и о вронскиане системы линейно независимых частных решений ЛОДУ. 45
2.8. Теорема о размерности пространства решений ЛОДУ n-го порядка. Фундаментальная система решений. Структура общего решения. 48
2.9. Формула Остроградского-Лиувилля для ЛОДУ n-го порядка и ее следствия. 49
2.10. Теорема о структуре общего решения неоднородного ЛДУ n-го порядка. Теорема о наложении частных решений 51
2.11. ЛОДУ с постоянным коэффициентами. Характеристическое уравнение и построение общего решения по его корням (вывод для 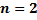 ). 51
). 51
2.12. Нахождение частных решений неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида. 54
2.13. Метод вариации постоянных решения неоднородных ЛДУ n -го порядка (вывод для 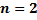 ). 57
). 57
2.14. Нормальные системы ДУ. Задача Коши и теорема существования и единственности ее решения. Сведение ДУ n -го порядка к нормальной системе. Сведение нормальной системы к одному уравнению n -го порядка. 59
2.15. Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов. 61
2.16. Нормальные системы ЛДУ, однородные и неоднородные. Матричная запись системы. Линейность пространства решений системы ЛОДУ. Вронскиан системы вектор-функций и его свойства. Теорема о размерности пространства решений системы ЛОДУ. Структура общего решения. Фундаментальная система решений. 66
2.17. Системы ЛОДУ с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения по корням характеристического уравнения (вывод для случая вещественных различных корней) . . 68
1. Интегральное исчисление функций одного переменного
1.1. Первообразная. Теоремы о первообразных. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов.
Опр. Функция 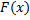 называется первообразной функции
называется первообразной функции 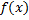 на
на 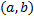 , если
, если 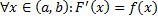 .
.
Пример. 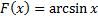 – первообразная функции
– первообразная функции 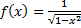 на интервале
на интервале 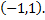
Теорема 1 (об арифметических свойствах первообразной).
Пусть 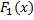 и
и 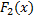 – первообразные функций
– первообразные функций 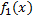 и
и 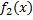 соответственно. Тогда функция
соответственно. Тогда функция 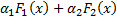 – первообразная функции
– первообразная функции 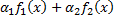 (
( 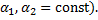
Док-во: 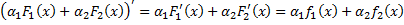 , т.е. функция
, т.е. функция 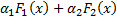 – первообразная функции
– первообразная функции 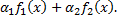

Теорема 2 (об общем виде первообразной).
Пусть 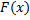 – первообразная функции
– первообразная функции 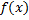 . Тогда любая первообразная функции
. Тогда любая первообразная функции 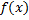 имеет вид
имеет вид
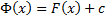 , где
, где 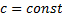
Док-во: т.к. 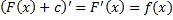 , то
, то 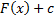 – тоже первообразная функции
– тоже первообразная функции 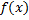 . Покажем, что любая первообразная имеет вид
. Покажем, что любая первообразная имеет вид 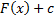 . Пусть
. Пусть 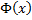 – первообразная функции
– первообразная функции 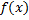 . Рассмотрим функцию
. Рассмотрим функцию 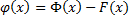 :
: 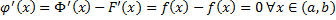 . Рассмотрим произвольные
. Рассмотрим произвольные 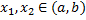 .
. 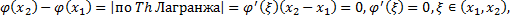 т.е.
т.е. 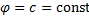 . Значит,
. Значит, 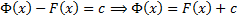
Опр. Совокупность всех первообразных функции 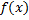 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 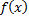 .
.
Обозн.: 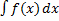 .
.
Пусть 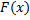 – первообразная функции
– первообразная функции 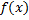 . Тогда
. Тогда 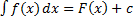 , где
, где 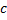 – произвольная постоянная.
– произвольная постоянная.
Пример. 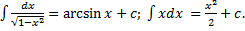
Свойства неопределенного интеграла:
1. 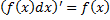
2. 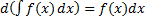
3. 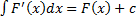 или
или 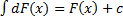
4. 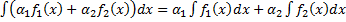 , где
, где 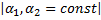
Док-во:
1. 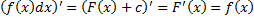 , где
, где 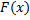 – первообразная функции
– первообразная функции 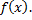
2. 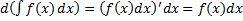 .
.
3. Т.к. 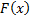 – первообразная
– первообразная 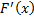 , то
, то 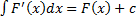 .
.
4. Пусть 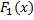 и
и 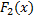 – первообразные функций
– первообразные функций 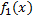 и
и 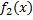 соответственно.
соответственно.
Тогда функция 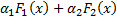 – первообразная функции
– первообразная функции 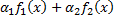 (
( 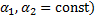 . Отсюда
. Отсюда 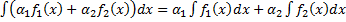

Таблица интегралов:
1. 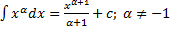
2. 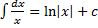 . (Т.к. при
. (Т.к. при 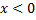
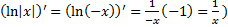
3. 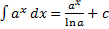 (
( 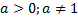 )
)
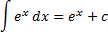
4. 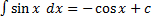
5. 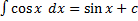
6. 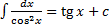
7. 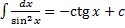
8. 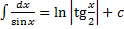
9. 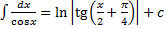
10. 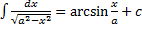 ,
, 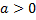
11. 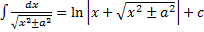 ,
, 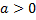 (длинный логарифм)
(длинный логарифм)
12. 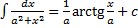 ,
,
13. 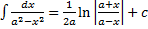 или
или 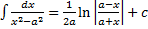 (высокий логарифм)
(высокий логарифм)
14. 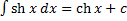
15. 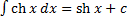
16. 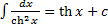
17. 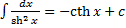
Примеры.
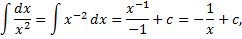
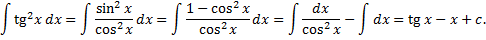
1.2. Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций.
Подведение под знак дифференциала.
Пусть 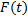 – первообразная функции
– первообразная функции 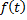 на
на 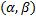 , т.е.
, т.е. 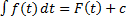 . Рассмотрим замену
. Рассмотрим замену 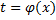 , где
, где 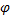 – дифференцируемая на
– дифференцируемая на 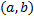 функция,
функция, 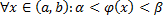 .
.
Рассмотрим сложную функцию 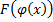 ,
, 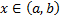 .
.
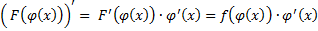 , т.е.
, т.е. 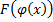 – первообразная для
– первообразная для 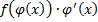 , т.е.
, т.е. 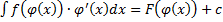 , или
, или 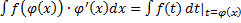 , или
, или 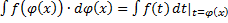 ,
,
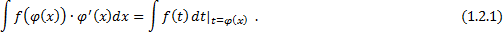
Примеры.
1. 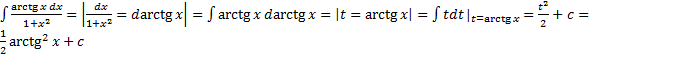
2. 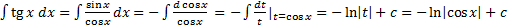
3. 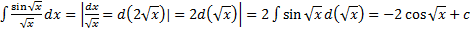 .
.
Замена переменной. Поменяем в (1.2.1) местами 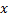 и
и 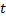 :
: 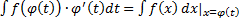 ,
,
где 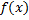 определена на
определена на 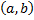 ,
, 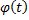 дифференцируема на
дифференцируема на 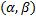 , причем
, причем 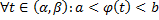 .
.
Пусть 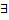 обратная функция
обратная функция 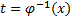 . Заменим
. Заменим 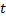 на
на 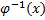 :
:
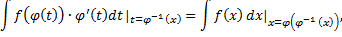
Т.е.
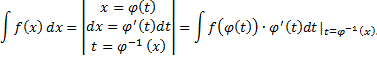
Пример.
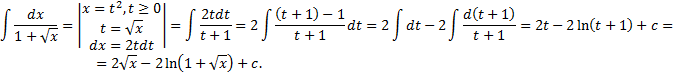
Интегрирование по частям
Пусть функции 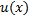 и
и 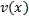 дифференцируемы на
дифференцируемы на 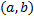 . Тогда
. Тогда 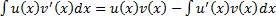 , т.е.
, т.е. 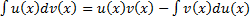
Док-во: 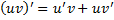 , т.е.
, т.е. 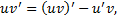
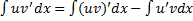 , т.е.
, т.е. 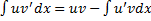 ,
,
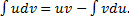

Примеры.
1. 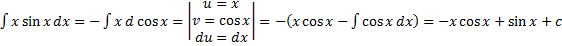 .
.
2. 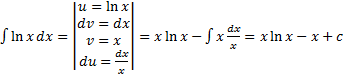 .
.
3. 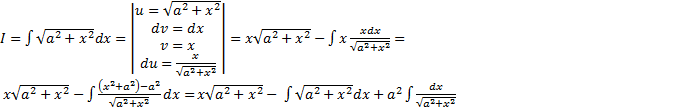 ,
,
т.е. 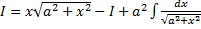 , т.е.
, т.е.
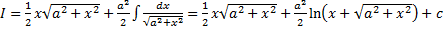 .
.
Интегрирование выражений, содержащих квадратный трехчлен
I. 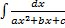 ,
, 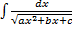 .
.
Выделим полный квадрат, получим табличный интеграл (10-13)
Примеры.
1. 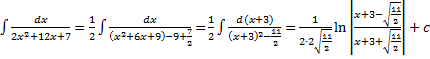 .
.
2. 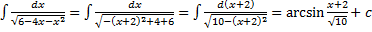 .
.
II. 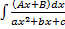 ,
, 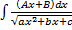 .
.
Выделим в числителе производную квадратного трехчлена 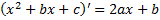 , т.е. представим числитель в виде
, т.е. представим числитель в виде 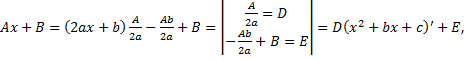
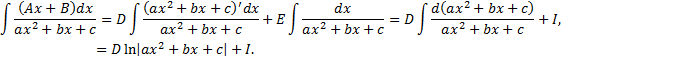
где 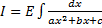 – находится с помощью выделения полного квадрата.
– находится с помощью выделения полного квадрата.
Аналогично
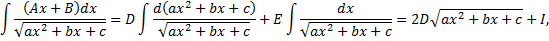
где 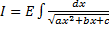 .
.
Примеры.
1. 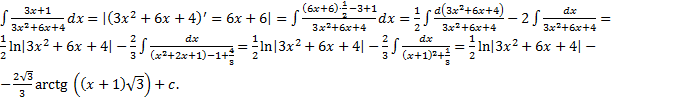
2.