ЛЕКЦИЯ 9. Понятие о различных методах расчёта сооружений на прочность. Расчёт стержней при растяжении-сжатии по предельной нагрузке

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Конструкция в течение всего срока эксплуатации должна нести нагрузки не разрушаясь и не испытывая недопустимо больших деформаций. Исходя из этих требований, а также с учётом экономии материала происходит подбор поперечных сечений. Необходимые размеры сечений определяются из условий прочности, жёсткости и устойчивости.

Расчёт на прочность сводится к требованию, чтобы наибольшие напряжения в элементе конструкции (нормальные, касательные, либо определённая комбинация этих напряжений) не превосходила некоторой допустимой для данного материала величины.

Существуют три метода расчёта на прочность:

1) метод допускаемых напряжений;

2) метод предельных состояний;

3) метод разрушающих нагрузок.

Первые два метода были рассмотрены ранее. Остановимся на третьем методе. Для конструкции, изготовленной из материала с достаточно протяженной площадкой текучести за разрушающую принимается нагрузка, при которой в её элементах возникают значительные пластические деформации. При этом конструкция становится неспособной воспринимать дальнейшее увеличение нагрузки.

Для конструкции, изготовленной из хрупкого материала, за разрушающую принимается нагрузка, при которой хотя бы в одном из её элементов возникают напряжения, равные пределу прочности 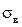. Так для стержня с постоянным поперечным сечением площади А за разрушающую нагрузку, в случае пластичного материала принимают F_s = σ _s A, а в случае хрупкого материала - .

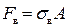Расчёт статически неопределимых систем при упруго-пластической работе материала. Расчёт аналогичных систем при упругой работе материала был рассмотрен на предыдущей лекции.

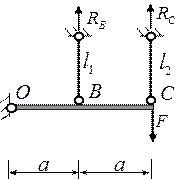Рис. 9.1.

Будем рассматривать состояние статически неопределимой системы, приведённой на рис. 9.1 при изменении внешней силы F от нуля до F_max – силы, при которой будет исчерпана несущая способность конструкции. Пусть материал подвесок будет одинаковым и подчиняющимся диаграмме Прандтля (рис. 8.3). Примем l₁ = l₂ = l. При упругой работе материала напряжения в подвесках составят 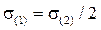(это следует из совместного решения уравнений (8.1) и (8.2)), т.е. вторая подвеска при любом значении силы более напряжена. Следовательно, по мере увеличения силы наступит момент, когда напряжение во втором стержне достигнет предела текучести σ₍₂₎ = σ_s. Силу можно увеличивать до предельного значения, при котором σ₍₁₎ = σ₍₂₎ = σ_s. При действии предельной нагрузки грузоподъёмность сооружения достигает максимума, наступает состояние предельного равновесия между внешними и внутренними силами. Это значит, что при малейшем превышении силой предельного значения, деформация подвесок начинает неограниченно возрастать и сооружение теряет геометрическую неизменяемость, превращаясь в механизм.

Для оценки прочности конструкции по предельному состоянию действующую силу сравнивают с некоторыми допускаемыми значениями, заниженными по сравнению с предельным значением нагрузки в связи с неоднородностью материала и неточностью определения его механических характеристик.

Расчет статически неопределимых стержневых систем при осевом растяжении-сжатии по предельной несущей способности

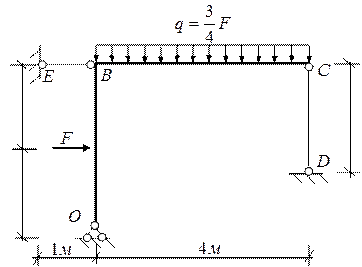
Дано: ОВС – жесткий стержень,

стержень ВЕ: Е_ВЕ=2×10⁵МПа,

R=200МПа, σ_s,ВЕ=300МПа, k=1,5

и площадь поперечного сечения А;

стержень СD: Е_СD=1×10⁵МПа,

R=120МПа, σ_s,СD=180МПа, k=1,5

и площадь поперечного сечения 2А;

Требуется: определить площадь

поперечного сечения А из условия прочности,

найти значение нагрузки F_s из расчета

по предельной несущей способности и F_adm.

Решение

Под действием нагрузки стержень ВЕ растягивается, а стержень СD сжимается, стержень ОВС поворачивается по ходу часовой стрелки относительно точки О. Точка В переходит в точку В₁ по дуге окружности, но в связи с малостью деформаций и небольшой кривизной дуги будем считать, что перемещение точки В осуществляется вдоль оси стержня ВЕ и составляет удлинение стержня. Точка С переходит в точку С₁ по дуге окружности (радиус окружности ОС=ОС₁), пренебрегаем малостью кривизны и принимаем, что перемещение точки С в С₁ происходит по прямой (СС₁ 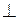ОС, СС₁ 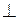ОС₁). Разложим перемещение точки С на два составляющих: сначала точка С вдоль оси стержня СD попадает в С₂, это перемещение составляет абсолютную деформацию стержня. Далее С₂ по перпендикуляру перемещается в С₁. Выполним чертеж, иллюстрирующий перемещение системы.

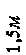
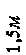
ОС=5м (египетский треугольник);

sinα=3/5=0,6;

cosα=4/5=0,8.

ΔОВВ₁ подобен ΔОСС₁

(по двум углам), тогда:

ВВ₁/ОВ=СС₁/ОС =>

=> ВВ₁=(ОВ×СС₁)/ОС,

ВВ₁=3СС₁/5,

Δl_ВЕ=0,6СС₁ (0).

I . Раскрытие статической неопределимости задачи

1. Рассмотрим статическую сторону задачи. Составим уравнения равновесия:

∑F_X=0; Н_О-R_Е+F=0 (1),

∑F_Y=0; V_О+R_D-2×4q=0 (2),

∑m_О=0; 1,5F+2×4q-4R_D-3R_Е=0 => 7,5F-4R_D-3R_Е=0 (3).

Уравнений статики – три, неизвестных опорных реакций – 4, тогда степень статической неопределимости n_st=4-3=1 – задача один раз статически неопределимая, т.е. требуется привлечь еще одно уравнение для раскрытия статической неопределимости.

2. Рассмотрим геометрическую сторону задачи. В случае изменения длин стержней ВЕ и СD, их абсолютные деформации составят: ВВ₁=Δl_ВЕ и СС₂=Δl_СD. Рассмотрим прямоугольный треугольник ΔСС₂С₁, выразим гипотенузу СС₁ через катет СС₂: СС₁=СС₂/cosα=СС₂/0,8=Δl_СD/0,8. Воспользуемся предыдущими вычислениями (0) и получим связь между и Δl_ВЕ = 0,6СС₁=0,6Δl_СD/0,8=0,75Δl_СD, итак Δl_ВЕ=0,75Δl_СD (4).

3. Рассмотрим физическую сторону задачи. Абсолютная деформация стержней вызвана действием нагрузок, поэтому её можно представить в виде следующей зависимости: Δl=Nl/ЕA (5). Следует отметить, что N_ВЕ=R_Е, N_СD=R_D.

Подставим (5) в (4) и получим уравнения совместности деформаций.

Δl_ВЕ=(N_ВЕl_ВЕ)/(Е_ВЕA_ВЕ)=(R_Е×1)/(2×10⁸А),

Δl_СD=(N_СDl_СD)/(Е_СDA_СD)=(R_D×2)/(1×10⁸2А). (6)

Подставим (4) в (6) и получим (R_Е×1)/(2×10⁸А)=0,75(R_D×2)/(1×10⁸2А), сократим на площадь А, тогда выражение примет вид: R_Е=1,5R_D (7). Решая совместно (3) и (7) поучим R_Е=1058,8кН, R_D=705,9кН.

Статическая неопределимость задачи раскрыта, далее задача решается как статически определимая.

II . Определение площади поперечного сечения

Запишем условия прочности для стержней ВЕ и СD, приравняем напряжение к расчетному сопротивлению и выразим площадь:

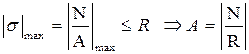. Найдем площадь для каждого стержня.

Необходимо учесть, заданное по условию задачи соотношение площадей: A_ВЕ=А=R_Е/R=1058,8/(200×10³)=52,9см² => А=52,9см²,

A_СD=2А=R_D/R=705,9/(200×10³)=58,8см² => А=29,4см².

Окончательно принимаем к расчету наибольшую площадь А=52,9см².

III. Расчет по предельной несущей способности

Найдем силу F_s, соответствующую предельному состоянию. Для этого используем уравнение (3) 7,5F-4R_D-3R_Е=0, подставив в него внутренние усилия, соответствующие предельному состоянию и выразим F_s.

N_ВЕ,s=σ_s,ВЕA_ВЕ=300×10³×52,9, N_СD,s=σ_s,СDA_СD=180×10³×2×52,9, тогда уравнение (3) примет вид: 7,5F_s-4(300×10³×52,9)-3(180×10³×2×52,9)=0

F_s=1653кН, тогда F_adm=F_s/k=1653/1,5=1102кН > 800кН.

Расчет по предельной несущей способности дает большие значения допустимой силы, чем расчет с использованием условий прочности и расчетных сопротивлений.