ЛЕКЦИЯ 16. Определение перемещений сечений балок. Расчёт на жёсткость. Расчёт статически неопределимых балок
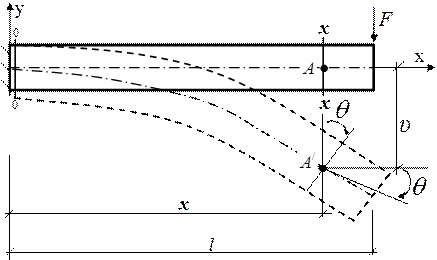При прямом поперечном изгибе все силы располагаются в одной из главных плоскостей и действуют перпендикулярно оси стержня. При такой деформации продольная ось искривляется и называется изогнутой или упругой осью балки. При этом возникают перемещения: прогибы ( v ) и углы поворотов (Θ) рис. (16.1). Уравнение кривой v = v (x) – уравнение изогнутой оси балки. На рисунке представлены отрицательные прогиб (перемещение вниз) и угол поворота (поворот по ходу часовой стрелки) сечения.
Рис. 16.1. Перемещения сечений балки при изгибе
Перемещения связаны между собой
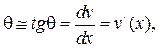(16.1)
т.е. уравнение углов поворота можно получить дифференцированием уравнения изогнутой оси балки. Воспользуемся зависимостью, полученной в предыдущей лекции.
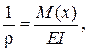(16.2)
здесь EI – изгибная жёсткость балки.
Воспользовавшись уравнением кривизны кривой можно получить
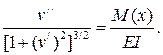(16.3)
Это уравнение достаточно сложное, т.к. v/ = θ, а при малых прогибах θ<<1, то величиной (v/)2 можно пренебречь по сравнению с 1, тогда (16.3) упростится до вида (16.4) и будет называться приближённым дифференциальным уравнением изогнутой оси балки
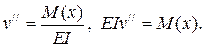(16.4)
Расчет на жесткость производят с помощью условий жесткости. Опираясь на них можно решать поверочную задачи (выполнять проверку выполнения условия) и проектную - определять размер поперечного сечения или подбирать допустимое значение параметра нагрузки.
Условия жесткости можно записать для прогибов (v) и углов поворота (Θ):
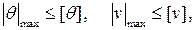(16.5)
где значения перемещений в квадратных скобках являются допустимыми, прогиб [v] = (1/200 ÷ 1/800)l/.
В случае, когда изгибная жёсткость постоянна во всех сечениях балки, то решение приближённого дифференциального уравнения изогнутой оси балки производится методом непосредственного интегрирования. Уравнение (16.4) интегрируется два раза, определяются две постоянные интегрирования при помощи граничных условий (условий закрепления балки). Для балки, приведённой на рис. 16.1. эти уравнения запишутся следующим образом.
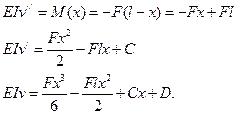
В заделке отсутствуют перемещения, граничные условия можно записать как: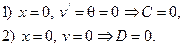 
В данном случае окончательный вид изогнутой оси
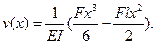
Максимальные перемещения получит свободный конец балки:
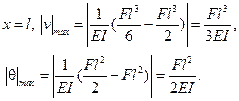
Если балка имеет несколько грузовых участков (рис. 16.2), то использовать метод непосредственного интегрирования сложно. В таких случаях используют уравнения метода начальных параметров (16.6), которые получены путем интегрирования дифференциального уравнения изогнутой оси балки (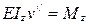 
). Для того, чтобы свести количество постоянных интегрирования к минимуму, т.е. к двум ( 
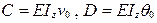), обязательно выполнение правил Клебша, некоторые из них приведены ниже.
1. Начало координат назначают строго на правом или левом конце балки.
2. При составлении уравнений рассматривают ту часть балки, которая содержит начало координат.
3. В случае, когда равномерно распределенная нагрузка прерывается в каком-то сечении, то часть балки между этим сечением и концом балки, противоположном началу координат, догружают и разгружают (компенсируют) равномерно распределенной нагрузкой той же интенсивности.
4. Если выражение (x-а i)n < 0, то член, содержащий этот полином, исключается из уравнения.
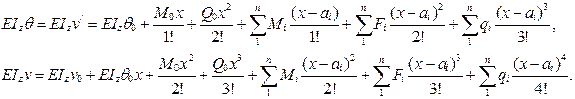(16.6)
Здесь v 0, Θ 0, М0, Q 0 – начальные параметры, x – расстояние от начала координат до сечения, в котором определяется перемещение, a – расстояние от начала координат до места приложения или начала действия нагрузки.
Правило знаков для нагрузок в (16.6) тоже, что и для изгибающих моментов.
 |
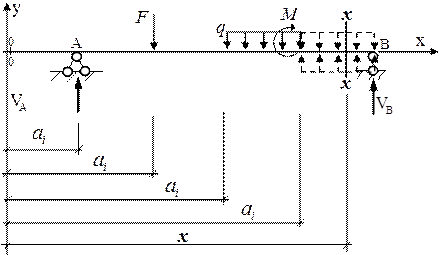Рис. 16.2. Балка, имеющая несколько грузовых участков
Расчёт статически неопределимых балок. Балка, у которой количество неизвестных опорных реакций превышает количество уравнений равновесия, называется статически неопределимой (рис. 16.3). По аналогии с осевым растяжением и кручением для решения статически неопределимых задач, т.е. для раскрытия их статической неопределимости, необходимо привлечь дополнительные уравнения. Количество этих уравнений зависит от степени статической неопределимости. В качестве дополнительных уравнений используют уравнения деформаций, выражающие связь между деформациями отдельных элементов системы, в данном случае - уравнения метода начальных параметров. При этом в универсальные уравнения метода начальных параметров вводят опорные реакции как неизвестные величины наряду с неизвестными кинематическими начальными параметрами. Все неизвестные определяются из уравнений равновесия и кинематических условий закрепления балки. Степень статической неопределимости ( nst ) – число связей, после устранения которых, балка превращается в статически определимую: nst=n-3, здесь n – число опорных реакций, 3 – количество уравнений статики.
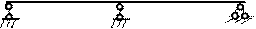а) nst=2 б) nst=1
Рис. 16.3. Статически неопределимые системы