ЛЕКЦИЯ 15. Касательные и главные напряжения при прямом поперечном изгибе. Полная проверка прочности
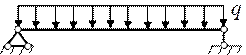
Касательные напряжения при изгибе. При прямом поперечном изгибе изгибающий момент и поперечная сила отличны от нуля, наличие этих внутренних усилий приводит к возникновению нормальных и касательных напряжений. Гипотеза плоских сечений не выполняется (рис. 15.1).
 а)
а)
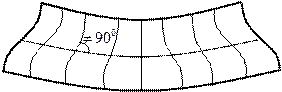 |
в)
 б)
б)
Рис. 15.1. а) схема нагружения балки при прямом поперечном изгибе, б) балка до деформации, в) балка после деформации
На решение задачи об определении нормальных напряжений при изгибе ушло 188 лет. В 1638г. эту задачу поставил Г. Галилей, а её правильное решение было изложено Навье в его учебнике «Сопротивление материалов» в 1826г. Зависимость для определения касательного напряжения при изгибе была получена в 1855г. выдающимся русским инженером Д.И. Журавским при разработке методов расчёта деревянных пролётных строений в ходе проектирования и строительства ж/д. Петербург – Москва.
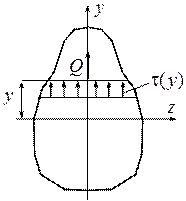 При выводе этой формулы он считал, что касательные напряжения распределяются равномерно по ширине поперечного сечения и направлены параллельно поперечной силе (рис. 15.2).
При выводе этой формулы он считал, что касательные напряжения распределяются равномерно по ширине поперечного сечения и направлены параллельно поперечной силе (рис. 15.2).
Рис. 15.2. Поперечное сечение произвольной формы
Вырежем элемент балки длиной dx (рис. 15.3), на расстоянии y от оси z проведём продольное сечение, рассмотрим нижнюю отсечённую часть. Внутренние усилия в поперечном сечении М и Q, на расстоянии dx внутренние силы в поперечном сечении составят М + d М и Q. Нормальные напряжения в любой точке сечения σ/ и на расстоянии dx σ// определяются с помощью зависимости 15.1.
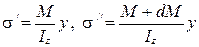 . (15.1)
. (15.1)
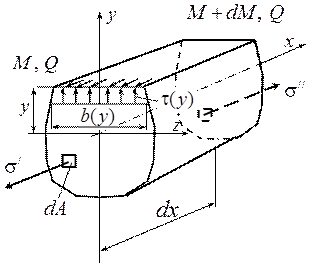 |
Рис. 15.3. Элемент балки
Элемент балки должен находиться в равновесии, поэтому
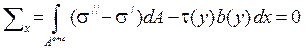
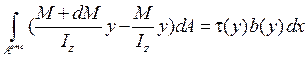
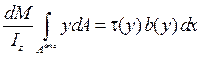
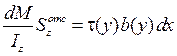
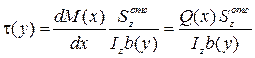
Окончательно формула Д.И. Журавского для определения касательных напряжений имеет вид (15.2).
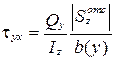 . (15.2)
. (15.2)
Касательное напряжение в конкретном сечении не зависит от отношения поперечной силы к осевому моменту инерции ( 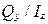 ), т.к. эта величина в пределах одного сечения не меняется, а зависит от отношения статического момента площади отсеченной части к ширине сечения на уровне отсеченной части (
), т.к. эта величина в пределах одного сечения не меняется, а зависит от отношения статического момента площади отсеченной части к ширине сечения на уровне отсеченной части ( 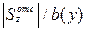 ).
).
Условие прочности по касательным напряжениям выглядит как:
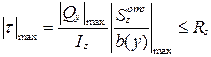 , (15.3)
, (15.3)
здесь обозначения такие же, что и в формуле Журавского, а Rs – расчетное сопротивление срезу или расчетное сопротивление по касательным напряжениям. Как правило 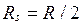 .
.
Главные напряжения. Сведения о главных напряжениях изложены ранее (лекция 3).
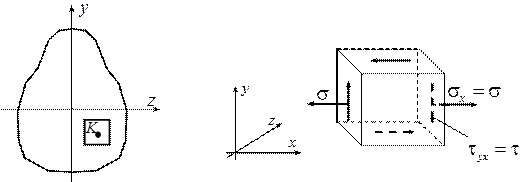 |
Рис. 15. 4. Иллюстрация плоского напряжённого состояния в точке
В случае плоского напряжённого состояния, к которому относится прямой поперечный изгиб σx = σ, σy = 0, τyx = τ, тогда тензор напряжений будет иметь вид
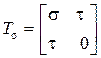 .
.
Ранее было получено, что
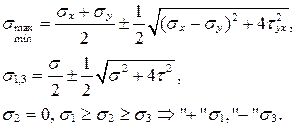 (15.4)
(15.4)
Подставим (15.4) в выражение для третьей теории прочности (теория наибольших касательных напряжений)
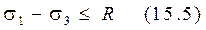
и получим условие прочности по третьей гипотезе прочности
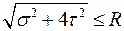 . (15.6)
. (15.6)
Можно воспользоваться четвёртой (энергетической теорией прочности), подставим (15.4) в (15.7) и получим (15.8) – условие прочности по энергетической теории.
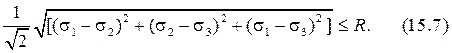
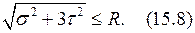
Полная проверка прочности при изгибе – это последовательная проверка прочности по нормальным, касательным и главным напряжениям, которые имеют вид:
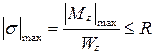 ,
, 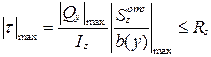 ,
, 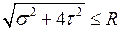 .
.








