ЛЕКЦИЯ № 7 (2курс) .Графические изображения выборки. Полигон и гистограмма. Выборочные характеристики.
ЛЕКЦИЯ № 7 (2курс) .Графические изображения выборки. Полигон и гистограмма. Выборочные характеристики.
План
- Основные понятия выборки.
- Графическое изображение выборки. Полигон и гистограмма.
- Выборочные характеристики.
4. Показатели здоровья населения.
5. Статистические показатели для оценки деятельности поликлиники и стационара.
Медицинская статистика - отрасль статистической науки
Математическая статистика является основой применения количественных методов анализа в различных сферах человеческой деятельности. В зависимости от объекта исследования имеются различные направления применения методов математической статистики. Большое внимание уделяется применению статистических методов для обработки медико-биологических данных. Этими вопросами занимается медицинская статистика.
Определение.
Медицинская статистика - отрасль социальной статистики, которая изучает количественные характеристики состояния здоровья населения, развития системы здравоохранения, определяет степень интенсивности влияния на них социально - экономических факторов, а также занимается
приложением статистических методов к обработке и анализу результатов клинических и лабораторных исследований.
Это определение взято из Статистического словаря, где также определены задачи медицинской статистики: своевременное получение и разработка данных о заболеваемости, смертности, инвалидности, физическом развитии населения в целом и отдельных его групп, о размещении, состоянии, оснащении, медицинских кадрах учреждений здравоохранения, клинических и
лабораторных исследованиях.
Таким образом, медицинская статистика оценивает показатели здоровья населения, здравоохранения, состояния окружающей среды для определения ее безопасности и влияния на здоровье человека.
В медицинской статистике выделяют следующие разделы:
статистику здоровья, изучающую санитарно-демографические процессы, динамику заболеваемости, физического развития, и статистику здравоохранения, изучающую деятельность медико-санитарных учреждений и медицинских кадров.
Источниками информации, позволяющими оценить основные показатели, являются: первичная учетная медицинская документация, которая ежедневно ведется в учреждениях здравоохранения; статистическая отчетность; лабораторные и клинические обследования. Вопросами сбора, обработки и хранения информации занимаются отделы статистики, которые входят в структуру медицинских организаций.
Медицинская статистика использует методы математической статистики, связанные с обработкой выборочных данных. В основе сбора медико- биологических данных лежит закон больших чисел, позволяющий при массовых обследованиях выявить наличие объективных закономерностей, лежащих в основе эпидемиологических, социальных, медицинских процессов.
Основными задачами медицинской статистики являются разработка специальных методов исследования массовых процессов и явлений в медицине и здравоохранении; выявление наиболее существенных закономерностей и тенденций в здоровье населения в целом и в различных его группах (возрастных, половых, профессиональных и др.) во взаимосвязи с конкретными условиями и образом жизни: изучение и оценка состояния и динамики развития сети, деятельности учреждений здравоохранения и медицинских кадров.
Интенсивный показатель определяет интенсивность развития (частоту, уровень, распространенность) явления в среде, которая продуцирует это явление.
Интенсивный показатель=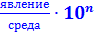 
(100; 1000; 10000 и т.д.)
Показатель интенсивности выражается:
v При основании 100 человек – в процентах (%);
v При основании 1000 человек – в промилле (%0)
v При основании 10000 человек – в продецимилле (%00)
v При основании 100 000 человек – в просантимилле (%000)
Выбор числового основания (100;1000;10000… и т.д.) зависит от распространенности явления - чем реже встречается изучаемое явление, тем большее основание выбирается, чтобы не было коэффициентов меньше единицы, которыми неудобно пользоваться. Например, на 1000 рассчитываются основные демографические показатели, первичная заболеваемость; на 100.000 - инфекционная заболеваемость, уровень заболеваемости туберкулезом, нервно - психической патологией и др.
Примерами интенсивных коэффициентов могут служить коэффициенты рождаемости, смертности, заболеваемости, инвалидности.
Вычисление интенсивных показателей производится следующим образом.
Например: население города Н. в 2005 г. составило 1.318.600 человек. В течение года умерло 22.944 человек. Для вычисления коэффициента смертности необходимо составить и решить следующую пропорцию:
1.318.600 - 22.944 22.944 · 1000
1000 - Х Х = ------------------ = 17,4 ‰.
1.318.600
При вычислении интенсивных коэффициентов мы всегда имеем дело с двумя самостоятельными, качественно различными совокупностями, одна из которых характеризует среду, а вторая - явление (например, число больных и число умерших); нельзя считать, что больные «распределились на выздоровевших и умерших», умершие - это новое (в данном случае необратимое) явление, самостоятельная совокупность.
Примеры применения интенсивных коэффициентов:
- определение уровня, частоты, распространенности того или иного явления;
- сравнение ряда различных совокупностей по степени частоты того или иного явления (например, сравнение уровней рождаемости в разных странах, сравнение уровней смертности в разных возрастных группах);
- выявление динамики изменений частоты явления в наблюдаемой совокупности (например, изменение распространенности инфекционных заболеваний населения страны за несколько лет).
Экстенсивный показатель характеризует распределение явления на его составленные части, его внутреннюю структуру или отношение частей к целому (удельный вес).
Экстенсивный показатель =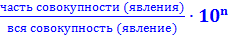 
Множитель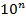 
зависит от распространенности явления в среде.
Чем реже явление встречается, тем больше множитель.
Вычисление экстенсивных коэффициентов производится следующим образом. Например: в 2005 г. население города Р. составило 1.318.600 человек, в том числе мужчин – 605.300 человек. Если принять все население города Р. за 100% , то доля мужчин составит:
1.318.600 - 100% 605.300 · 100
605.300 - Х Х = -------------------- = 45,9%
1.318.600
Экстенсивными коэффициентами можно характеризовать структуру рождаемости (распределение родившихся по полу, росту, весу); структуру смертности (распределение умерших по возрасту, полу и причинам смерти); структуру заболеваемости (распределение больных по нозологическим формам); состав населения по полу, возрасту и социальным группам и др.
Характерной чертой экстенсивных коэффициентов является их взаимосвязанность, вызывающая определенный автоматизм сдвигов, т.к. их сумма всегда составляет 100%. Например, при изучении структуры заболеваемости удельный вес какого-нибудь отдельного заболевания может возрасти в следующих случаях:
1) при подлинном его росте, т.е. при увеличении интенсивного показателя;
2) при одном и том же его уровне, если число других заболеваний в этот период снизилось;
3) при снижении уровня данного заболевания, если уменьшение числа других заболеваний происходило более быстрыми темпами.
Экстенсивные коэффициенты дают представление об удельном весе того или иного заболевания (или класса болезней) только в данной группе населения и только за определенный период.