Определение момента инерции в машине атвуда

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

ОТЧЕТ

по лабораторно-практической работе № 5

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
В МАШИНЕ АТВУДА

Выполнил Гладких Н.А.

Факультет ЭА

Группа № 3401

Преподаватель Морозов В.В

“Выполнено” “____” ___________Подпись преподавателя __________

ЛАБОРАТОРНАЯ РАБОТА № 5

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ В МАШИНЕ АТВУДА

Цель работы: изучение вращательного и поступательного движений на машине Атвуда, определение момента инерции блока и момента сил трения в оси блока.

Описание установки и её назначение.

Машина Атвуда является настольным прибором, ее изображение приведено на рис. 3.1. На вертикальной стойке 1 основания 2 расположены три кронштейна: нижний 3, средний 4 и верхний 5. На верхнем кронштейне 5 крепится блок с узлом подшипников качения, через который переброшена нить с грузом 6. На верхнем кронштейне находится электромагнит 7, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии.

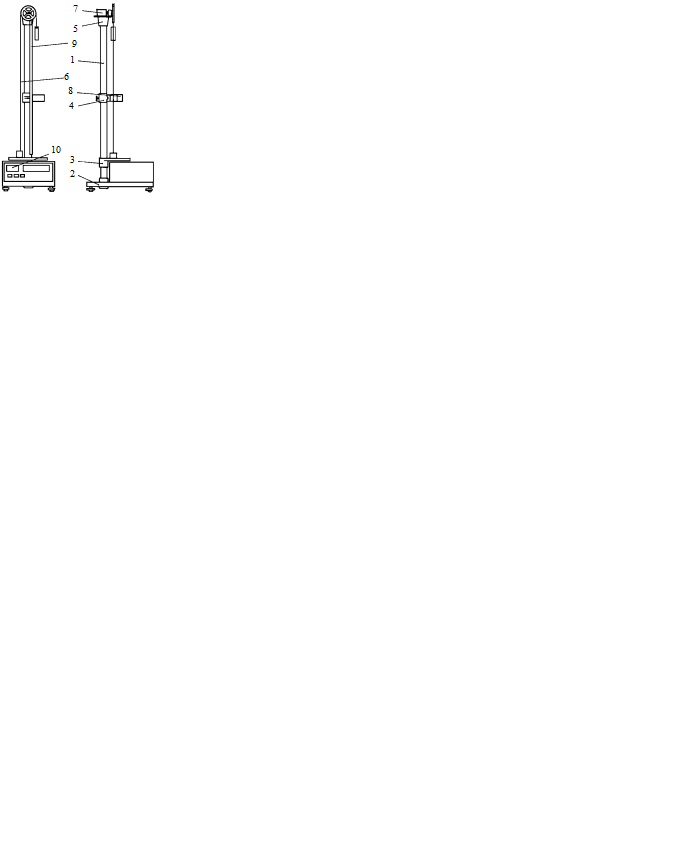Рис. 3.1

На среднем кронштейне 4 крепится фотодатчик 8, выдающий электрический сигнал по окончании счета времени равноускоренного движения грузов. Также на вертикальной стойке 1 укреплена миллиметровая линейка 9, по которой определяют начальное и конечное положения грузов, т. е. пройденный путь.

Начальное положение определяют визуально по нижнему краю груза, конечное положение – по риске среднего кронштейна. Секундомер 10 выполнен как самостоятельный прибор с цифровой индикацией времени.

Машина Атвуда предназначена для изучения законов поступательного и вращательного движений. Принцип работы установки основан на том, что, когда на концах нити подвешены грузы различной массы, система начинает двигаться равноускоренно. В комплект грузов входит несколько перегрузов, что позволяет исследовать движения с различными ускорениями.

Основные расчетные формулы.

1) М= ( T1 – T2) r – Mтр = I e - уравнение, описывающее вращение блока. Где r – радиус блока; Mтр – момент сил трения в оси блока; I – момент инерции блока; e – угловое ускорение блока.

2) M = r (( m1 + D m_i) ( g – a) – m2( g + a)) – развернутая формула 1. Где m1 и m2 – массы 1-го и 2-го грузов; Dmi – масса перегруза, находящегося на 1-м грузе; a – ускорение грузов.

3) a = 2S / t² - формула для определения ускорения грузов.

e = a / r = 2 S / (r t2) – формула для определения углового ускорения блока.

S = h0 – h1 - путь.

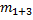
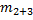
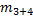
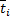; с	1,841	1,718	1,333	1,124	1,044
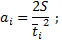
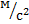
	0,177	0,203	0,338	0,475	0,572
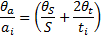
	0,442	0,450	0,483	0,511	0,529
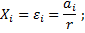
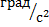
	4,318	4,958	8,326	11,583	13,956
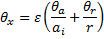
	2,012	2,350	4,229	6,208	7,717
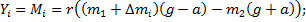
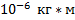
	181	167	188	732	846
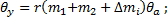
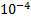
	5	6	10	16	19
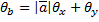
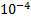
	7	8	13	21	25

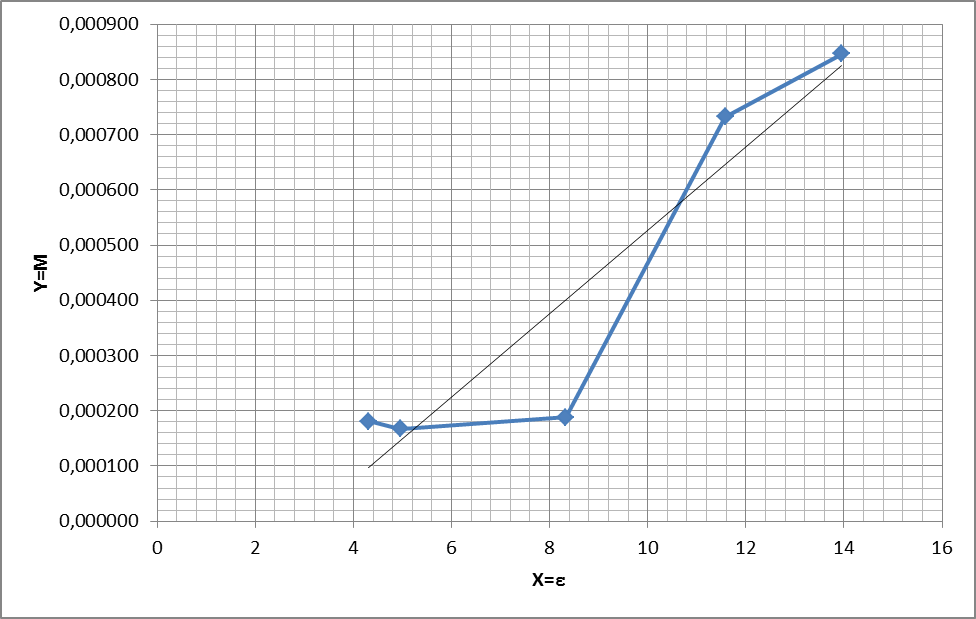
Из сопоставлений линейной зависимости 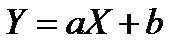и уравнения (3) получим

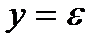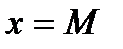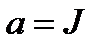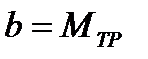; ; ; (7)

Вычислим параметры линейной зависимости по формулам МНК.

Среднее значение X(M), Y( ):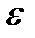

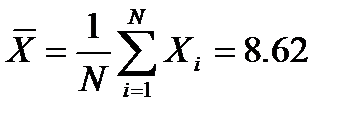
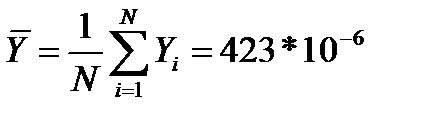
Вычисляем среднее значение коэффициентов а и b:

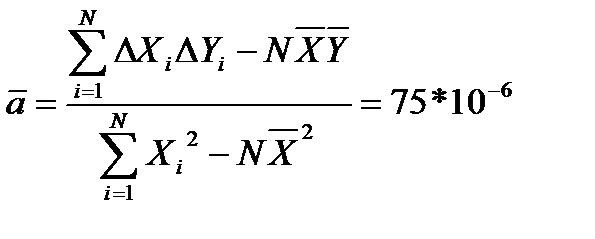
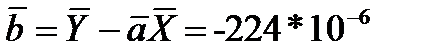
Вычисляем средние квадратические отклонения для средних 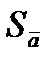и :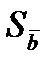

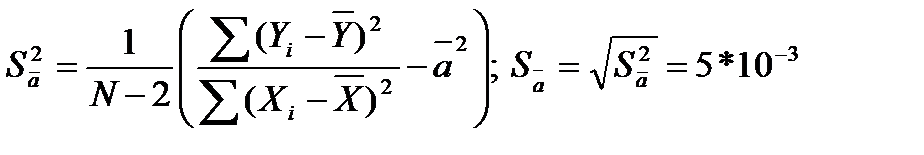
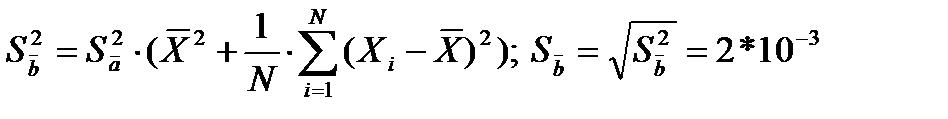
Вычисляем доверительную погрешность 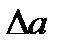и 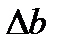для Р=95%:

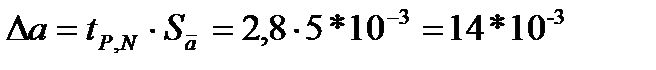
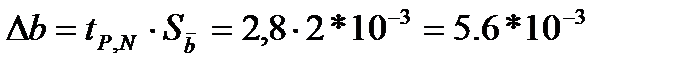
Полные погрешности a и b :

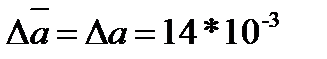
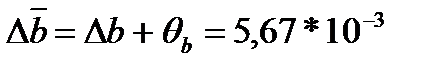
Из соотношения (7) получим:

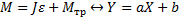
Окончательный результат в округленной форме:

Y=aX+b