Двухслойные перцептроны и их обучение

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

ЛАБОРАТОРНАЯ РАБОТА №5

ДВУХСЛОЙНЫЕ ПЕРЦЕПТРОНЫ И ИХ ОБУЧЕНИЕ

ЦЕЛЬ: Приобретение и закрепление знаний и получение практических навыков работы с многослойными перцептронами на примере двухслойного элементарного перцептрона.

Теоретические сведения

Одним из методов распознавания образов основан на моделировании гипотетического механизма человеческого мозга. При таком подходе уровень биологических знаний или гипотез о биологических механизмах является исходной предпосылкой, на которой базируются модели этих механизмов. Примером такого направления в теории и практике проблемы распознавания образов является класс устройств, называемых перцептронами. Нужно отметить, что перцептроны на заре своего возникновения рассматривались только как эвристические модели механизма мозга. Впоследствии они стали основополагающей схемой в построении кусочно-линейных моделей, обучающихся распознаванию образов.

В наиболее простом виде перцептрон представлен на рис. 1.

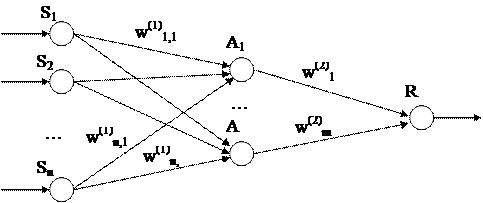Рис.1. Элементарный персептрон.

Он состоит из совокупности чувствительных (сенсорных) элементов (S-элементов), на которые поступают входные сигналы (входной вектор). S-элементы соединены с совокупностью ассоциативных элементов (А-элементов) связями c весовыми коэффициентами w⁽¹⁾_i_,_j, в свою очередь А-элементы соединены с реагирующим элементом (R-элементом) связями с весовыми коэффициентами w⁽²⁾_j, выход которого составляет реакцию системы, которая указывает на принадлежность распознаваемого объекта (входного вектора) определенному классу.

Перцептрон называется элементарным, если: (а) он имеет единственный R-элемент, связанный со всеми А-элементами связями с переменными весами, (б) имеются только последовательные (в одном направлении) связи между S- и A-элементами и между A- и R-элементами, (в) веса связей между S- и A-элементами являются фиксированными.

Функционирование перцептрона происходит следующим образом. На вход перцептрона подаются сигналы в бинарном виде, которые передаются на А-элементы, умножаясь на весовые коэффициенты первого слоя и суммируясь:

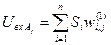, (1)

где S_i – значение i-го входа перцептрона, 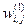- вес связи между i-ым S-элементом и j-ым А-элементом.

Сигналы на выходах А-элементов формируются следующим образом:

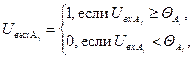(2)

где 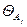- порог срабатывания j-го А-элемента.

Далее выходы А-нейронов передаются на R-элемент, умножаясь на весовые коэффициенты второго слоя и суммируясь:

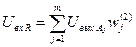, (3)

где 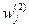- вес связи между j-ым A-элементом и R-элементом.

Выходной сигнал перцептрона формируется следующим образом:

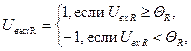(4)

где 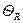- порог срабатывания R-элемента.

Поскольку на выходе элементарного перцептрона могут быть только два значения выходного сигнала, он может применяться для разделения множества входных векторов на два класса.

Обучение элементарного перцептрона выполняется следующим образом:

1. Выбирается количество A-элементов (эмпирически), равное или меньшее количеству входов перцептрона.

2. Случайным образом инициируются веса связей нейронов первого слоя (между S- и A-элементами), например, из диапазона [0.1, 1].

3. Для каждого из входных векторов обучающего множества вычисляются значения 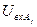в соответствии с формулой (1).

4. Для каждого А-элемента выбираются пороги срабатывания 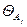так, чтобы наибольшее число А-нейронов реагировало по-разному при предъявлении изображений разных классов. Реакция А-нейронов вычисляется по формуле (2).

Пример: пусть задано 2 входных вектора X и Y , относящихся к разным классам, и количество А-элементов равно 6.

Допустим, что при подаче на вход перцептрона входных изображений получаются следующие значения :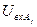

Класс изображения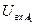
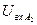
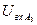
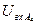
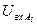
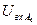
I (X)	3.5	3.6	3.5	3.4	3.3	3.2
II (Y)	3.2	3.2	3.5	3.2	3.6	3.5

Если выбрать пороги 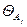более 3.6 или менее 3.2, то в соответствии с формулой (2) все A -элементы будут реагировать на оба класса изображений одинаково, разделение изображений на классы в этом случае невозможно. Выберем порог 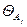= 3.5 для всех А-элементов.

В этом случае при подаче на вход перцептрона изображения X первого класса X активными будут нейроны А₁, А₂ и А₃, а при подаче изображения Y второго класса - нейроны А₃, А₅ и А₆.

В идеальном случае пересечение множеств активности А-элементов для разных классов пустое.

В случае, если множества активности А-элементов совпадают и подобрать пороги срабатывания 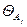не удается, следует переинициализировать веса связей А-элементов или задать другое их количество.

5. Случайным образом инициируются веса связей нейронов второго слоя (между А- и R-элементами), например, из диапазона [0.1, 1].

6. Выбирается значение порога срабатывания R-элемента 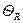(например, 0.5m).

7. Каждый класс сопоставляется с определенным желаемым значением выходного сигнала перцептрона. (например, для первого класса изображений выходным сигналом обученного перцептрона должна быть +1, для второго класса – должна быть -1).

8. Выполняется процедура изменения весов второго слоя 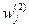для каждого входного вектора обучающего множества до тех пор, пока перцептрон не начнет правильно классифицировать все входные изображения.

Существуют следующие процедуры коррекции весов второго слоя перцептрона:

а) α-система подкреплений.

Заключается в том, что веса всех связей, начинающихся на активном для данного класса А-элементе (активных связей), изменяются на некоторую постоянную величину Δ.

Знак изменения весов для изображения С класса V определяется по формуле:

sign (R^*(С) - R(С)), (5)

где R^*(С) – желаемый выход перцептрона для изображений класса V, R(С) – реально полученный выход перцептрона при подаче на вход изображения С.

Пример (для вышеуказанных изображений X и Y ): пусть для первого класса изображений выходным сигналом обученного перцептрона должна быть +1, для второго класса – должна быть -1. Пусть значение порога 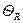= 2 и величина Δ=0.1.

Предположим, что при подаче изображения X на вход перцептрона значение 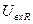, вычисленное по формуле (3), равно 1.8. В соответствии с формулой (4), R ( X )= 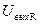=-1. Поскольку X относится к первому классу, то R ^* ( X )=+1.

Следовательно, по формуле (5) sign ( R ^* ( X ) - R ( X )) = 1, и веса связей, идущих от А-элементов, входящих в множество активности для изображения Х (это элементы А₁, А₂ и А₃- см. выше), будут увеличены на величину Δ. Такими весами являются веса 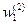, 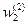и .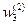

б) γ-система подкреплений.

Является модификацией предыдущей α-системы подкреплений, призванной исключить неконтролируемые увеличения или уменьшения отдельных весов связей. В соответствии с такой системой сначала веса активных связей увеличиваются (уменьшаются) на величину Δ (как в α-системе подкреплений), а затем все веса (активных и неактивных связей) уменьшаются (увеличиваются) на величину, равную модулю полного изменения весов активных связей, деленному на общее количество связей второго слоя. В этом случае общая сумма весов второго слоя остается неизменной.

в) метод коррекции случайными возмущениями.

Состоит в том, что знак и величина изменения весов активных связей являются независимыми, случайными и задаются каким-нибудь распределением (например, нормальным).

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

3.1. В соответствии с заданным вариантом:

· создать два класса изображений на основе первых двух букв фамилии студента. В каждый класс должно входить по три различных изображения;

· выбрать архитектуру двухслойного перцептрона;

· разработать и реализовать алгоритмы обучения двухслойного перцептрона распознаванию заданных классов букв с использованием различных способов процедур настройки весов;

· исследовать обучаемость и качество распознавания входных изображений при различных количествах А-элементов. Результаты отразить в табличном или графическом виде.

СОДЕРЖАНИЕ ОТЧЕТА

4.1. Тема лабораторных занятий.

4.2. Индивидуальное задание.

4.3. Результаты выполнения пункта 3.1 индивидуального задания.

4.4. Файл работающей программы для демонстрации ее возможностей.

Контрольные вопросы

Определение перцептрона и методы его обучения
Обучение перцептрона с помощью альфа-системы подкрепления
Обучение перцептрона с помощью гамма-системы подкрепления
Проблема исключающего ИЛИ и возможности многослойных перцептронов