Тема: Производные и дифференциалы высших порядков. Формула Лейбница
Теоретическая часть
1. Производная и дифференциал второго порядка
а) обратной функции;
б) функции, заданной неявно;
в) функции, заданной параметрически.
2. Формулы производных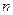 
-го порядка основных элементарных функций:
а)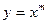 
;
б)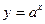 
;
в)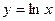 
;
г)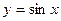 
;
д)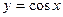 
.
3. Формула Лейбница 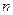-ой производной произведения двух функций.
Практическая часть
1. Найти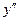 
и 
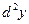функции, заданной неявно /2, стр. 125/.
1.1. № 63. 1.2. №64. 1.3. №65. 1.4. №66. 1.5. №67. 1.6. №68.
2. Найт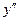и и 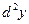функции, заданной параметрически /3/.
2.1. №1140. 2.2. №1141. 2.3. №1142.
2.4. №1143. 2.5. №1144. 2.6. №1142.
3. Найти производную 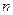-го порядка функции
3.1.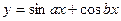 
. 3.2. 
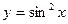. 3.3. 
.
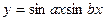3.4.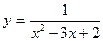 
. 3.5. 
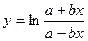. 3.6. 
.
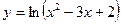4. Найти производную 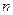-го порядка функции по формуле Лейбница
/2, стр. 124-125/.
4.1. № 46. 4.2. №47. 4.3. №50. 4.4. №51. 4.5. №49. 4.6. №54.
5. Найти 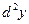функции 
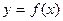, считая 
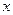промежуточным аргументом,
5.1.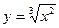 
. 5.2. 
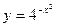. 5.3. 
.
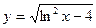5.4. 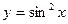. 5.5. 
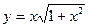. 5.6. 
.
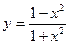Лабораторная работа №12
Тема: Исследование функций и построение их графиков
Теоретическая часть
1. Определение точки локального экстремума.
2. Необходимое условие экстремума.
3. Теоремы о первом и втором достаточных условиях экстремума.
4. Определение точки перегиба и необходимое условие перегиба.
5. Теоремы о первом и втором достаточных условиях перегиба.
6. Определение асимптоты кривой (наклонной, вертикальной и горизонтальной).
7. Теорема о необходимом и достаточном условиях существования наклонной асимптоты.
Практическая часть
1. Найти промежутки возрастания и убывания функции и выделить её точки экстремума /2, стр. 127/.
1.1. №107 (з). 1.2. №107 (г). 1.3. №107 (д).
1.4. №107 (е). 1.5. №107 (и). 1.6. №107 (к).
2. Найти наклонную асимптоту кривой /2, стр. 87/.
2.1. №174 (а). 2.2. №174 (б). 2.3. №174 (в).
2.4. №174 (г). 2.5. №174 (д). 2.6. №174 (ж).
3-4. Исследовать функции и начертить их графики /2, стр.132/.
3.1..№166. 3.2. №167. 3.3. №169. 3.4. №171. 3.5. №172. 3.6. №173.
4.1. №184. 4.2. №185. 4.3. №189. 4.4. №182. 4.5. №181. 4.6. №179.
Лабораторная работа №13
Тема: Разложение функции по формуле Тейлора
Теоретическая часть
1. Теорема Тейлора.
2. Формула Тейлора и формула Маклорена.
3. Остаточный член формулы Тейлора
а) в форме Пеано;
б) в форме Лагранжа;
в) в форме Коши.
4. Разложения по формуле Маклорена основных элементарных функций с остаточным членом в форме Пеано
а)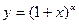 
;
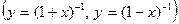б)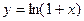 
;
в)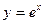 
;
г) ;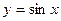
д) .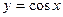
Практическая часть
1. Разложить функцию по формуле Маклорена с остаточным членом в форме Пеано. 
1.1.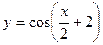 
. 1.2. 
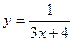. 1.3. 
.
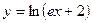1.4.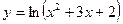 
. 1.5. 
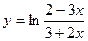. 1.6. 
.
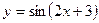2. Разложить функцию по формуле Тейлора в окрестности точки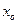 
с остаточным членом в форме Пеано.
2.1.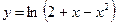 
, 
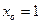. 2.2. 
, .
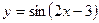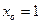2.3.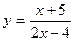 
, 
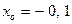. 2.4. 
, 
.
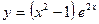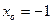2.5.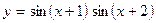 
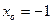, . 2.6. 
, 
.
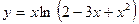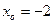3. Разложить функцию по формуле Маклорена с остаточным членом в форме Пеано.
3.1.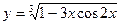 
. 3.2. 
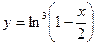. 3.3. 
.
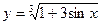3.4.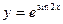 
. 3.5. 
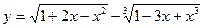. 3.6. 
.
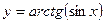4. Разложить функцию, заданную неявно, по формуле Тейлора с остаточным членом в форме Пеано.
4.1.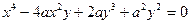 
, 
, 
.
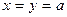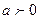4.2.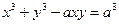 
, 
, 
.
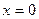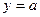4.3.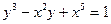 
, 
, 
.
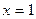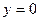4.4.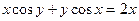 
, 
.
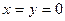4.5.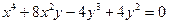 
, 
.
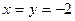4.6.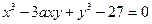 
, , 
.
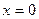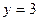5. Найти предел, используя правило Лопиталя /2, стр.131/.
5.1. №154. 5.2. №155. 5.3. №158. 5.4. №160. 5.5. №161. 5.6. №164.
Лабораторная работа №14
Тема: Приложения формулы Тейлора
Теоретическая часть
1. Главная часть разложения функции в окрестности данной точки по формуле Тейлора (по формуле Маклорена).
2. Оценка остаточного члена в форме Лагранжа в разложениях по формуле Маклорена основных элементарных функций
а) ,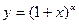 
;
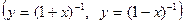б) ;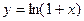
в) ;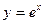
г) ;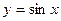
д) .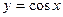
3. Оценка погрешности приближённого вычисления значения функции в точке по формуле Тейлора.
Практическая часть
1. Найти главную часть вида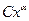 
при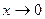 
функции /2, стр. 78/.
1.1. №6 (б). 1.2. №6 (г). 1.3. №6 (в).
1.4. №6 (д). 1.5. №6 (з). 1.6. №6 (ж).
2. Найти главную часть вида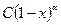 
при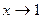 
функции /2, стр. 78/.
2.1. №7 (б). 2.2. №7 (г). 2.3. №7 (е).
2.4. №7 (и). 2.5. №7 (з). 2.6. №7 (в).
3. Найти главную часть вида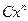 
при 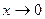функции /2, стр. 85/.
3.1. №139 (а). 3.2. №139 (б). 3.3. №139 (г).
3.4. №139 (д). 3.5. №139 (е). 3.6. №139 (з).