Тема: Производная. Дифференцируемость функции в точке. Дифференциал
Теоретическая часть
1. Определение производной функции в точке.
2. Определения односторонних производных функции в точке.
3. Определение дифференцируемости функции в точке.
4. Определение дифференциала.
5. Инвариантность формы первого дифференциала.
6. Теорема о необходимом и достаточном условии дифференцируемости функции в точке.
7. Теорема о непрерывности дифференцируемой функции.
Практическая часть
1. Используя определение производной, найти производную функции.
1.1.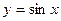 
. 1.2. 
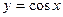. 1.3. 
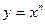. 1.4. 
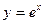. 1.5. 
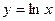. 1.6. 
.
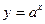2. Найт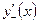и 
и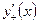 
функции /2, стр. 124/.
2.1. №36. 2.2. №37. 2.3. №38. 2.4. №39. 2.5. №40. 2.6. №41.
3. Найти числа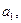 
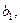
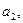
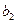так, чтобы функция была дифференцируема на всей числовой прямой /2, стр. 120-121/.
3.1. №34 (a). 3.2. №34 (б). 3.3. №34 (в).
3.4. №34(г). 3.5. №34 (а). 3.6. №34 (б).
4. Исследовать на дифференцируемость функцию
4.1.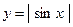 
. 4.2. 
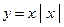. 4.3. 
.
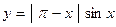4.4.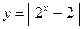 
. 4.5. 
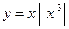. 4.6. 
.
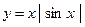5. Найти производную и построить графики функции и её производной /3/.
5.1. №977(в). 5.2. №979. 5.3. №980. 5.4. №981. 5.5. №982. 5.6. №983.
6. Найти дифференциал функции
6.1.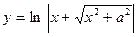 
. 6.2. 
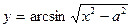. 6.3. 
.
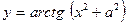6.4.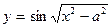 
. 6.5. 
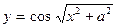. 6.6. 
.
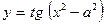Лабораторная работа №9
Тема: Техника вычисления производных и дифференциалов
Теоретическая часть
1. Формула производной суммы двух функций.
2. Формула производной произведения двух функций.
3. Формула производной частного двух функций.
4. Формула производной обратной функции.
5. Формула производной функции, заданной неявно.
6. Формула производной функции, заданной параметрически.
7. Производная и дифференциал сложной функции.
Практическая часть
1. Найти производную функции /2, стр. 123/.
1.1. №25. 1.2. №26. 1.3. №27. 1.4. №28. 1.5. №29. 1.6.№27.
2. Найти производную первого порядка функции, заданной параметрически
/2, стр. 125/.
2.1. №55. 2.2. №56. 2.3. №57. 2.4. №58. 2.5. №59. 2.6. №60.
3. Найти производную первого порядка функции, заданной неявно /2, стр. 125/.
3.1. №68. 3.2. №67. 3.3. №66. 3.4. №65. 3.5. №64. 3.6. №63.
4. Найти производную обратной функции в указанной точке.
4.1.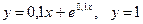 
. 4.2. 
.
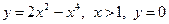4.3.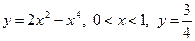 
. 4.4. 
.
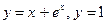4.5.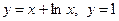 
. 4.6. 
.
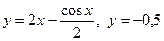5. Сделать указанную замену переменных в выражении
5.1.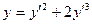 
, 
.
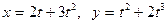5.2.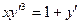 
, 
.
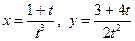5.3.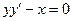 
, 
.
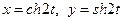5.4.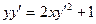 
, 
.
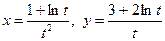5.5.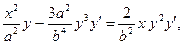 
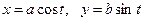
5.6.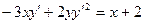 
, 
.
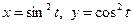6. Найти дифференциал функции
6.1.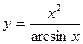 
. 6.2. 
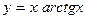. 6.3. 
.
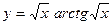6.4.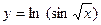 
. 6.5. 
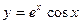. 6.6. 
.
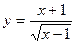Лабораторная работа №10
Тема: Приложения производной и дифференциала
Теоретическая часть
1. Геометрический смысл производной.
2. Физический смысл производной.
3. Уравнения касательной и нормали к кривой. Угол между кривыми.
4. Наибольшее и наименьшее значения функции.
5. Геометрический смысл дифференциала.
6. Приближенное вычисление с помощью дифференциала.
7. Оценка погрешности (абсолютная и относительная).
Практическая часть
1-3. Написать уравнения касательной и нормали в заданной точке /2, стр. 126/.
1.1. №80 (а). 1.2. №83 (а). 1.3. №85 (б).
1.4. №86 (а). 1.5. №83 (б). 1.6. №86 (б).
2.1. №81(б). 2.2. №82 (б). 2.3. №89 (а).
2.4. №81 (в). 2.5. №82 (в). 2.6. №89 (в).
3.1. №84. 3.2. №87. 3.3. №88.
3.4. №84. 3.5. №87. 3.6. №88.
4. Найти угол между кривыми /2, стр. 126/.
4.1. №90. 4.2. №91. 4.3. №93. 4.4. №94. 4.5. №95. 4.6. №103.
5. Найти наибольшее и наименьшее значения функции на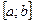 
/2, стр.128/.
5.1. №109.I (а). 5.2. №109.I (б). 5.3. №109.I (в).
5.4. №109.II (а). 5.5. №109.II (б). 5.6. №109.II (в).
6. Вычислить приближенно с помощью дифференциала
6.1.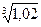 
. 6.2. 
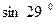. 6.3. 
.
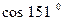6.4.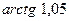 
. 6.5. 
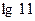. 6.6. 
.
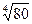Лабораторная работа №11