3. Даны натуральные числа m и n. Найти наименьшее общее кратное этих чисел.
Лабораторная работа №3. Циклы.
1. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу (например 153=13+53+33). Получить все числа Армстронга, состоящие из четырех цифр.
2. Числа Фибоначчи определяются формулами:
f0=f1=1; fn=fn-1+fn-2, n=2,3,...
Составить программу поиска fn - первого числа Фибоначчи, большего M.
3. Даны натуральные числа m и n. Найти наименьшее общее кратное этих чисел.
4. Напечатать все простые числа до 1000.
5. Дано действительное число x (x<1). Вычислить бесконечную сумму с заданной точностью (ε=0.0001). Считать, что требуемая точность достигнута, если очередное слагаемое оказалось по модулю меньше чем ε.
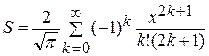
Дополнительные задания:
1.1. Дано натуральное число n. Найти сумму первой и последней цифры этого числа.
1.2. Дано натуральное k. Напечатать k-ю цифру последовательности 12345678910111213, в которой выписаны подряд все натуральные числа.
2.1 Дано натуральное число n. Переставить местами первую и последнюю цифры этого числа.
2.2. Дано натуральное k. Напечатать k-ю цифру последовательности 149162536, в которой выписаны подряд квадраты всех натуральных чисел.
3.1. Даны два натуральных числа m и n (m,n≤MaxInt). Проверить, есть ли в записи числа m цифры, одинаковые с цифрами в записи числа n.
3.2. Составить программу перевода натурального числа из десятичной системы счисления в двоичную.
4.1. Дано натуральное число n. Проверить, есть ли в записи числа три одинаковые цифры (n≤MaxInt).
4.2. Дано натуральное число n. Переставить его цифры так, чтобы образовалось максимальное число, записанное теми же цифрами.
5.1. Дано натуральное число n≤1000000. Дописать к нему цифру k в конец и в начало.
5.2. Найти все натуральные числа, не превосходящие заданного n, которые делятся на каждую из своих цифр.
6.1. Среди всех n-значных чисел указать те, сумма цифр которых равна данному числу k.
6.2. Найдите целые числа, которые при возведении в квадрат дают палиндромы, например, 262=676.
7.1. Заданы три натуральных числа A, B, C, которые обозначают число, месяц и год. Найти порядковый номер даты, начиная отсчет с начала года.
7.2. Составьте программу для вычисления самого большого числа, для которого можно вычислить факториал на имеющемся компьютере.
8.1. Найти наибольшую и наименьшую цифры в записи данного натурального числа n.
8.2. Найдите целые числа-палиндромы, которые при возведении в квадрат также дают палиндромы (222=484).
9.1. Произведение n первых нечетных чисел равно p. Сколько сомножителей взято? Если введенное n не является указанным произведением, сообщить об этом.
9.2. Найдите целые числа, которые при возведении в 3, или 4, или 5 степень дают палиндромы, например, 113=1331.








