В детерминированном факторном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1.Аддитивные модели: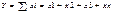 
, где Y – результативный показатель; ∑xi – сумма факторных показателей.
2.Мультипликативные модели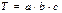 
, где
T – результативный показатель; a, b, c – факторные показатели.
3.Кратные модели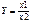 
, они применяются, когда результативный показатель получают делением факторных показателей.
4.Смешенные (комбинированные) модели.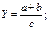 
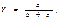
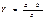и т.д.
Для выявления влияния факторов в детерминированном факторном анализе наиболее универсальным является прием цепных подстановок и арифметических разниц. Он основан на методе элиминирования. Элиминировать – значить устранить, исключить воздействие всех факторов на результативный показатель, кроме одного. Сначала изменяется один, а все другие остаются без изменения, потом изменяются два, три и т.д. такой прием позволяет определить влияние каждого фактора на величины исследуемого показателя в отдельности.
Используя способ цепной подстановки, рекомендуется придерживаться определенной последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. От того, в какой последовательности происходит замена, будет зависеть результат разложения. Значимость факторного анализа с использованием жестко детерминированных моделей заключается в точности оценок:
В идентификации факторов, влияющих на некоторый результативный показатель; В объяснении сути зависимости между признаками; В выявлении тенденций и относительной значимости факторов; В приблизительной степени оценки их влияния.
13.Традиционные методы экономической статистики.
В группу методов экономической статистики включают:
- метод средних величин;
- метод группировок;
- элементарные методы обработки расчетных данных;
- индексный метод.
Элементарные методы обработки расчетных данных. При изучении совокупности изучаемых величин помимо средних величин используют и другие характеристики.
При изучении массивов данных обычно интересуются двумя аспектами:
- величинами, которые характеризуют ряд значений, как целого; величинами, которые описывают различия между членами совокупности.
Все средние относятся к первой группе показателей, т.к. характеризуют совокупность в целом. Кроме тог, в качестве показателей общности используются следующие величины: середина интервала, мода, медиана.
Середина интервала: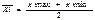 
.
Мода – такое значение признака, которое среди всех его значений встречается наиболее часто. Если в совокупности два признака встречаются наиболее часто – то совокупность бимодальна. Если в совокупности наиболее часто встречаются более двух признаков – то совокупность мультимодальна.
Медиана – такое значение изучаемой величины, которое делит анализируемую совокупность на две равные величины, в которых количество членов со значениями, большими значения медианы, равно количеству членов со значениями, меньше медианы.
14. метод средних величин.