1 задание: построить граф и его матрицу смежности без учета ориентации дуг

Дата: 2025-05-01; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

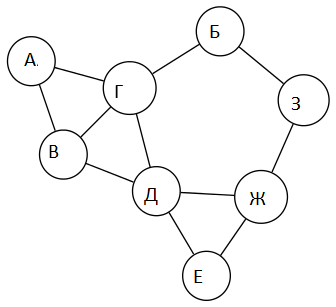
2 задание: Указать ориентацию дуг и построить новую матрицу смежности

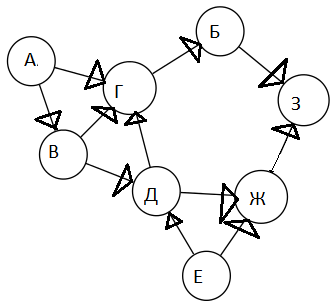
3 задание: Обозначить дуги и построить матрицу инциденций

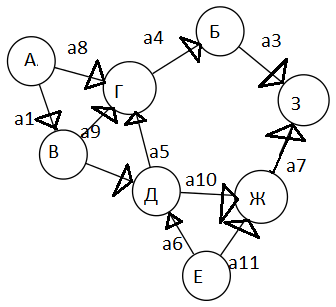
	а1	а2	а3	а4	а5	а6	а7	а8	а9	а10	a11
А	+1	0	0	0	0	0	0	+1	0	0	0
Б	0	+1	0	-1	0	0	0	0	0	0	0
В	-1	0	+1	0	0	0	0	0	+1	0	0
Г	0	0	0	+1	-1	0	0	-1	-1	0	0
Д	0	0	-1	0	+1	-1	0	0	0	+1	0
Е	0	0	0	0	0	+1	0	0	0	0	+1
Ж	0	0	0	0	0	0	+1	0	0	-1	-1
З	0	-1	0	0	0	0	-1	0	0	0	0

4 задание: указать все возможные маршруты между первым и последним элементами

1) А-Г-Б-З

2)А-В-Г-Б-З

3)А-В-Д-Г-Б-З

4) А-В-Д-Ж-З

5 Задание: указать основные свойства графа

1) Элементы группы находятся во взаимно однозначном соответствии с вершинами графа.

2) Каждое ребро графической сети есть направленный отрезок одного «цвета» связанные одной и той же образующей группы

3) Каждое слово, предоставляющая элемент группы, можно интерпретировать, как путь или некоторую последовательность направленных отрезков графа, и наоборот.

4) Умножение двух элементов группы соответствует из двух последовательных путей

5) Любое слово, предоставляющее элемент I, соответствует пути на графе.

6) Граф группы является сетью, т.е. существует путь из любой вершины в любую другую вершину.

Дновский Егор группа 6361