5. Примеры расчета показателя колебательности
Лабораторная работа 1
1Создать титульный лист
2Отформатировать текст согласно ГОСТ НИР.
3Текст должен содержать, рисунки, формулы, таблицы.
Федеральное Государственное Бюджетное образовательное учреждение Высшего профессионального образования Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова
Рекомендация кафедры «Систем обработки информации и управления» на статью Исакова Л.С., Куриловой Е.А.
«Оценка качества следящих систем показателем колебательности»
Статья посвящена актуальному вопросу оценке качества систем автоматического управления. Авторами разработана методика оценки качества следящих систем, описываемых уравнениями второго порядка, с помощью показателя колебательности. Статья подготовлена по результатам отработки курса «Радиоавтоматика». Методика используется при курсовом проектировании систем радиоавтоматики.
Новые научные результаты можно сформулировать в следующем виде:
Получены выражения, раскрывающие связи временных показателей качества с показателем колебательности.
Получены выражения для расчета показателей колебательности систем, скорректированных отрицательной обратной связью по скорости и форсирующей RC-цепью.
Кафедра рекомендует опубликовать статью в журнале «Известия вузов. Приборостроение»
УДК 531.391.3
Л.С. Исаков, Е.А. Курилова
Оценка качества следящих систем показателем колебательности
Показана аналогия свойств и отношений между последовательным колебательным контуром и следящей системой второго порядка. Получены выражения для оценки показателей колебательности нескорректированных и скорректированных следящих систем второго порядка. Исследованы связи временных показателей качества с показателем колебательности.
Приводятся примеры расчета показателя колебательности систем второго порядка с различными элементами коррекции.
Система, элемент, слежение, качество, показатель, колебательность, частота, добротность, коррекция, демпфирование.
Л.С. Исаков, Е.А. Курилова
Оценка качества следящих систем показателем колебательности
Понятие показателя колебательности.
О системах, в которых под действием внешних сил могут возникать колебания, говорят, что они имеют свойство колебательности. Мерой колебательности систем в физике и теории колебаний [1] принято считать добротность колебательной системы. Добротность определяется по амплитудно-частотной характеристики как отношение максимальной амплитуды колебаний (Amax) к амплитуде колебаний на нулевой частоте (A0)
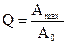
В теории автоматического управления, колебательность системы принято оценивать показателем колебательности (2), который определяется аналогично по амплитудно-частотной характеристике замкнутой системы
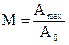
Как видно, показатель колебательности систем автоматического управления является аналогом добротности колебательных систем.
Оценка колебательности систем второго порядка
Общий подход к оценке колебательности состоит в построении амплитудно-частотной характеристики системы и получения отношения (1).
Однако для некоторых колебательных систем получены выражения для расчета добротности по значениям параметров системы. Рассмотрим оценку колебательности последовательного колебательного контура. Уравнение свободных колебаний тока в контуре имеет вид
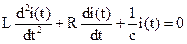
где L,C,R – индуктивность, емкость, активное сопротивление контура.
Колебательность контура оценивают следующей формулой добротности [3]
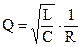
В теории колебаний коэффициент при второй производной принято называть инерционным коэффициентом (Cu), для колебательного контура Cu=L.
Коэффициент при первой производной называют коэффициентом демпфировния (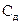 
), для колебательного контура 
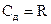. Коэффициент при колеблющейся переменной называют коэффициентом квазиупругости ( 
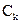), для колебательного контура 
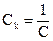. С учетом этих обозначений формула добротности колебательной системы второго порядка может быть записана в виде
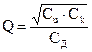
Рассмотрим оценку колебательности следящей системы на примере нескорректированной системы передачи угла с электронным усилителем и двигателем постоянного тока Рис
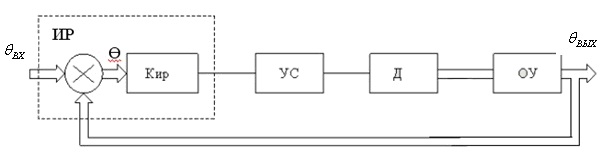
РИС Система передачи угла с электронным усилителем и
двигателем постоянного тока
В состав системы входят: объект управления (ОУ), исполнительный двигатель (Д), усилитель (УС) и измеритель рассогласования (ИР).
Колебания переходной ошибки в такой системе можно описать уравнением [4]
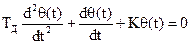
где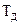 
– постоянная времени двигателя, K− коэффициент передачи разомкнутой системы, 
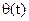.− угол ошибки (рассогласования).
Будем считать, что система должна обеспечивать слежение за вращением входной оси. В этом случае коэффициент передачи определяется выражением
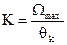
где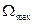 
− максимальное значение скорости вращения входной оси, 
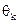− заданная кинетическая ошибка.
Для системы передачи угла инерционный коэффициент Cu=Tд, коэффициент демпфирования Cд=1, коэффициент квазиупругости Ck=k.
Показатель колебательности такой системы в соответствии с (3) определяется выражением
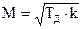
Запишем уравнение колебаний переходной ошибки (4) в приведенном виде
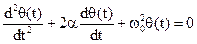
где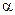 
− коэффициент затухания колебаний, 
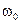− собственная частота без учета затухания.
Из сравнения (7) и (4) следует
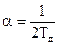
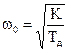
В соответствии с (3) показатель колебательности связан с параметрами колебаний следующим выражением
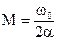
Формулой (10) удобно пользоваться при сравнительной оценке качества систем. Точность оценки зависит от соотношения между параметрами колебаний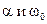 
. Так относительная погрешность оценки при 
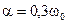составляет 5% и снижается при уменьшении .
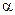Связь показателя колебательности с временными показателями качества
К временным показателям качества относят:
время переходного процесса (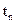 
),
перерегулирование (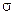 
),
число колебаний за время переходного процесса (N).
На примере системы второго порядка можно показать как временные показатели качества связаны с показателем колебательности.
Используем выражения (9) и (10), а также выражения временных показателей качества от параметров колебаний [2]: (формулы без нумерации)
времени переходного процесса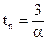 
,
перерегулирования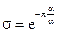 
,
числа колебаний за время переходного процесса,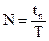 
,
где T – период колебаний,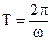 
.
Получим выражения, определяющие зависимость временных показателей качества от показателя колебательности.
Время переходного процесса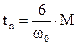 
Перерегулирование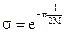 
Число колебаний за время переходного процесса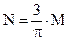 
Таким образом, значением показателя колебательности определяются значения временных показателей качества, т. е. показатель колебательности выступает как обобщенный показатель качества следящих систем. Для систем 2-го порядка при заданном значении M временные показатели качества определяются выражениями (11)-(13).
4. Оценка колебательности скорректированных систем
Общая формула показателя колебательности следящих систем второго порядка аналогична формуле (3)
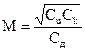
Из (14) видно как нужно менять параметры системы, чтоб изменить ее показатель колебательности. Изменения параметров осуществляют путем введения в систему элементов коррекции. Обычно требуется показатель колебательности уменьшить. Как следует из (14) для этого нужно увеличить коэффициент демпфирования, что осуществляется путем введения местной отрицательной обратной связи по скорости. Коэффициент демпфирования при этом определяется по формуле
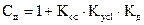где 
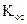− коэффициент передачи канала обратной связи; 
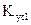− коэффициент передачи каналов усилителя, через которые проходит сигнал обратной связи; 
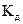− коэффициент передачи двигателя.
Из (15) получим формулу для определения коэффициента обратной связи
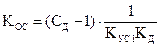
Для системы с отрицательной обратной связью по скорости формула показателя колебательности (14) с учетом (6) примет следующий вид
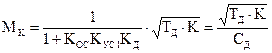где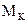 
− показатель колебательности скорректированной системы.
Формулу (17) с учетом (6) можно представить в виде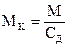 
Из (18) можно найти коэффициент демпфирования, обеспечивающий требуемый показатель колебательности
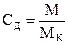
Вторым способом уменьшения показателя колебательности является уменьшение инерционного коэффициента. Это осуществляется применением, например, форсирующей RC-цепи, уменьшающий инерционный коэффициент. При этом формула (6) примет вид
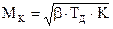где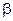 
− коэффициент передачи форсирующей RC-цепи, 
.
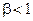В этом случае коэффициент затухания следует определять по формуле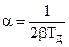 
, а собственную частоту без учета затухания по формуле (без нумерации)
.
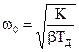Формулу (20) можно представить в виде
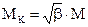
Из (21) получим формулу коэффициента передачи форсирующей RC-цепи
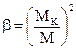
5. Примеры расчета показателя колебательности
Параметры функциональных элементов:
.
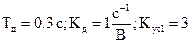Требования к показателям качества:
.
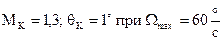Определить параметры элементов коррекции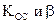 
, обеспечивающие требования к качеству, и временные показатели.
В соответствии с (5) коэффициент передачи разомкнутой системы
.
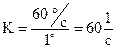5.1 Нескорректированная система
По формуле (6) показатель колебательности составляет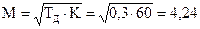 
.
По формулам (11)-(13) временные показатели составляют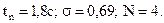 
5.2 Система с коррекцией по скорости
По формулам (16) и (19) находим коэффициент обратной связи, обеспечивающий значение показателя колебательности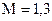 
.
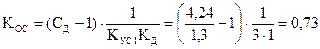
По формулам (11)-(13) находим временные показатели качества
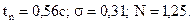
5.3 Система с коррекцией форсирующей RC-цепью
По формуле (22) находим коэффициент передачи цепи, обеспечивающий значение показателя колебательности .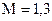
.
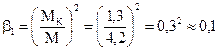По формулам (11) - (13) временные показатели составляют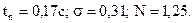 
Заключение
1. Получены выражения для расчета показателей колебательности нескорректированных и скорректированных следящих систем, описываемых уравнениями второго порядка.
2. Получены выражения, определяющие связи временных показателей качества с показателем колебательности.
3. Приведены примеры определения показателя колебательности и временных показателей качества для систем с различными элементами коррекции.
Список литературы
Хайкин С.Э., Физические основы механики. М: Наука, 1971.
Бесекерский В.А. Попов Е.П., Теория систем автоматического управления. СПб, Изд-во Профессия, 2003.
Баскаков С.Н., Радиотехнические цепи и сигналы. М: Высшая школа, 1983.
Исаков Л.С. Курилова Е.А., Основы теории систем радиоавтоматики, Балт. гос. техн. Ун-т. – СПб, 2012.