Средняя длина кода из таблицы 1 будет равна
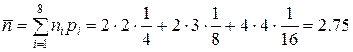 бит,
бит,
что совпадает со значением энтропии:
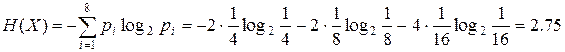 бит.
бит.
Еще одним способом построения оптимальных кодов является метод Хаффмана. Код Хаффмана строится следующим образом:
1) располагают символы в порядке убывания их вероятностей;
2) складывают вероятности двух последних символов и из них образуют новый составной символ с вероятностью, равной получившейся сумме;
3) повторяют шаги 1 и 2, пока не останется только один символ с вероятностью 1;
4) приписывают компонентам составных символов 0 и 1 – первой компоненте приписывают 0, а второй – 1.
Покажем процесс построения кодов Хаффмена для алфавита сообщений
X = (x1, x2, x3, x4, x5, x6, x7, x8)
с распределением вероятностей появления символов
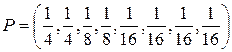 .
.
1. Исходный список букв X = {x1, x2, x3, x4, x5, x6, x7, x8} уже упорядочен, так как 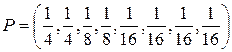 .
.
2. Объединим буквы x7 и x8 в одну букву x1 с вероятностью 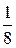 и переупорядочим список:
и переупорядочим список:
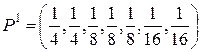 , X1 = {x1, x2, x3, x4, x1, x5, x6}.
, X1 = {x1, x2, x3, x4, x1, x5, x6}.
3. Повторим шаг 2 до тех пор, пока не останется одна буква в списке:
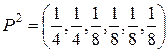 , X2 = {x1, x2, x3, x4, x1, x2};
, X2 = {x1, x2, x3, x4, x1, x2};
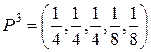 , X3 = {x1, x2, x3, x3, x4};
, X3 = {x1, x2, x3, x3, x4};
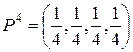 , X4 = {x1, x2, x3, x4};
, X4 = {x1, x2, x3, x4};
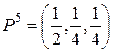 , X5 = {x5, x1, x2};
, X5 = {x5, x1, x2};
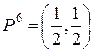 , X6 = {x5, x6};
, X6 = {x5, x6};
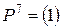 , X7 = {x7}.
, X7 = {x7}.
4. Присвоим двоичные коды символам:
x7: x5 = 0, x6 = 1;
x6: x1 = 10, x2 = 11;
x5: x3 = 00, x4 = 01;
x4: x3 = 010, x4 = 011;
x3: x1 = 000, x2 = 001;
x2: x5 = 0010, x6 = 0011;
x1: x7 = 0000, x8 = 0001.
Таким образом, получены следующие коды исходных символов:
x1 = 10, x2 = 11, x3 = 010, x4 = 011, x5 = 0010, x6 = 0011, x7 = 0000, x8 = 0001.
Средняя длина кода равна
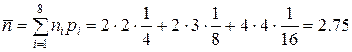 бит,
бит,
что совпадает со средней длиной кода Шеннона-Фано и с энтропией.
Способом добиться наименьшей средней длины кода на один символ является блочное кодирование. При блочном кодировании коды присваиваются не отдельным символам сообщений, а их сочетаниям. При увеличении числа символов в сочетании средняя длина кода на один символ приближается к энтропии. Например, пусть имеются две буквы алфавита – A и B, с вероятностями появления 0.9 и 0.1 соответственно. Закодировать их можно, присвоив 0 одному символу и 1 – другому:
A = 0, B = 1.
Средняя длина кода в этом случае будет равна 1 биту:
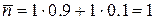 ,
,
тогда как энтропия равна
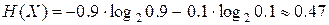 бит.
бит.
Избыточность составляет около 53%. Если же закодировать двухбуквенные сочетания XiXj, Xi, Xj Î {A, B} с вероятностями p(XiXj) =pipj, то по методу Шеннона-Фано можно получить коды, представленные в таблице 2.
Таблица 2
Блочное кодирование Шеннона-Фано
| XiXj | pipj | Шаг | Код | ||
| 1 | 2 | 3 | |||
| AA | 0.81 | 0 | ¾ | ¾ | 0 |
| AB | 0.09 | 0 | ¾ | 10 | |
| BA | 0.09 | 1 | 1 | 0 | 110 |
| BB | 0.01 | 1 | 111 | ||
Тогда средняя длина кода двухбуквенного блока будет равна 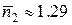 бит, а на одну букву будет приходиться
бит, а на одну букву будет приходиться 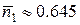 бит. Избыточность в этом случае будет составлять уже только около 17%. Если мы возьмем сочетания из трех букв, то получим еще лучший результат и т.д. Увеличивая длину блоков можно как угодно близко приблизиться к оптимальному значению энтропии.
бит. Избыточность в этом случае будет составлять уже только около 17%. Если мы возьмем сочетания из трех букв, то получим еще лучший результат и т.д. Увеличивая длину блоков можно как угодно близко приблизиться к оптимальному значению энтропии.
2. Порядок выполнения лабораторной работы
1. Ознакомиться с основными сведениями об оптимальном кодировании.
2. Получить задание на выполнение лабораторной работы.
3. Выполнить необходимые расчеты.
4. Сделать выводы о свойствах кодов.
5. Оформить отчет о выполнении лабораторной работы.
6. Ответить на контрольные вопросы.
3. Контрольные вопросы
1. В чем заключается кодирование и декодирование сообщений?
2. Что такое префиксные коды?
3. В чем заключается неравенство Крафта?
4. Как определить нижний предел средней длины кода?
5. Каковы принципы построения оптимальных кодов?
6. При каком условии равномерный код будет оптимальным?
7. Как построить коды Шеннона-Фано?
8. Как построить коды Хаффмена?
9. В чем заключается блочное кодирование?
4. Задания на лабораторную работу
1. Определить вероятности появления символов заданного источника с алфавитом A = {a, b, c, d} из таблицы 3 (использовать частоты символов).
2. Определить энтропию сообщения.
3. Построить коды Шеннона-Фано и Хаффмана для отдельных символов.
4. Построить коды Шеннона-Фано и Хаффмана для двухбуквенных блоков символов.
5. Закодировать сообщение.
6. Декодировать сообщение.
7. Определить среднюю длину и избыточность для всех кодов.
8. Определить наиболее оптимальное кодирование для источника сообщений.
Таблица 3
Сообщения дискретного источника
| № | Сообщение |
| 1 | abcaaaabacabbacbbaccbbaccbbddadadaa |
| 2 | bcabbcdabacbbacbbddcbbaccbbdbdadaac |
| 3 | aaabacabbacbbaccabcabbaccbbddadadaa |
| 4 | abcaaaaabbacbaacccabaccbbaccbbddadd |
| 5 | aaddaddabacabbacbbaccbbaccbbddadada |
| 6 | cccaddabbbaccaabcaaaabacabbacbbacbb |
| 7 | dbdaadabacabbacbbaccbbaccbbddadadac |
| 8 | bbbbbaabacabbacbbaccbbacdbbddadadac |
| 9 | aacabaaaacdbbacbddccbbaccbbddadadbb |
| 10 | dddaadabbbabbacbbaccbbaccbbddadddaa |
| 11 | abcccccbacabbacbbaddbdaccbbddadadcc |
| 12 | abcbbbbbacabbacddacdbbaccbbadadaddd |








