Антенны и распространение радиоволн
МИНОБРНАУКИ РОССИИ
–––––––––––––––––––––––––––––––––
Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»
–––––––––––––––––––––––––––––––––––––––
АНТЕННЫ И РАСПРОСТРАНЕНИЕ
РАДИОВОЛН
Лабораторный практикум
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2014
УДК 621.396.67(07)
ББК
Авторы: В. С. Алексеев, С. В. Балландович, С. В. Грачев, Г. А. Костиков, К. П. Наумов, И. Н. Семенихин, М. И. Сугак.
Н00 Антенны и распространение радиоволн: Лабораторный практикум. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2014. 88 с.
ISBN 978-5-7629- -
Представлены описания семи лабораторных работ по дисциплине «Антенны и распространение радиоволн», посвященных изучению электродинамических характеристик некоторых типов антенных устройств.
Предназначена для студентов факультета радиотехники и телекоммуникаций направлений 210400 "Радиотехника", 210700 "Инфокоммуникационные технологии и системы связи"а также специальности 210601.65 "Радиоэлектронные системы и комплексы".
УДК
ББК
Рецензенты: кафедра радиотехники Сибирского филиала РАН,
к.т.н. начальник лаборатории ОАО "НПП Радар ммс" О.С. Миронов
Утверждено
редакционно-издательским советом университета
в качестве учебного пособия
 ISBN 978-5-7629- - © СПбГЭТУ «ЛЭТИ», 2014
ISBN 978-5-7629- - © СПбГЭТУ «ЛЭТИ», 2014
1. АНТЕННАЯ СИСТЕМА ИЗ АКТИВНОГО
И ПАССИВНОГО ВИБРАТОРОВ
1.1. Введение, теоретические сведения
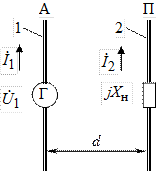
В данной лабораторной работе исследуется антенная система, состоящая из двух параллельных полуволновых вибраторов, один из которых (активный) возбуждается по фидеру от генератора, а другой (пассивный) нагружен в центре на реактивное регулируемое сопротивление (рис. 1.1, 1.2). Для минимизации потерь в качестве нагрузки используется короткозамкнутый шлейф, т. е. отрезок двухпроводной экранированной линии с подвижной перемычкой. Пассивный элемент может настраиваться таким образом, что антенна преимущественно излучает в его направлении, в этом случае он называется директором, а режим работы всей системы – директорным. Возможна и иная настройка системы, при которой наблюдается максимальное излучение в направлении противоположном пассивному элементу, в этом случае он называется рефлектором, а режим работы – рефлекторным (рис. 1.3). В ходе выполнения работы экспериментально и теоретически исследуются оба этих режима.

| 
|
| Рис. 1.1 | Рис. 1.2 |
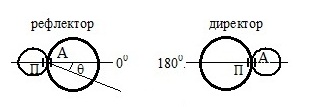
Рис. 1.3
В практических конструкциях таких антенн (они имеют и другое название – антенны «волновой канал», или антенны «Уда-Яги») в большинстве случаев настройку пассивных элементов осуществляют выбором их длины. В этом случае, рефлектор немного длиннее активного элемента, а директор – короче. В данной работе длины вибраторов одинаковые, а настройка пассивного элемента по методическим соображениям осуществляется исключительно выбором длины шлейфа.
Принцип работы направленной двухэлементной антенны заключается в синфазном сложении полей в направлении главного максимума и в противофазном сложении (т. е. в подавлении результирующего поля) – в противоположенном направлении. При пассивном питании (через взаимное влияние по полю) вспомогательного элемента имеет место не идеальная синфазность или противофазность полей, однако диаграмма направленности (ДН) системы может сохранять приемлемую для практических задач форму. Фаза тока (и поля излучения) пассивного излучателя, зависит от величины и знака реактивной нагрузки в нем или от его длины в случае, когда нагрузка отсутствует. Адекватное математическое описание данной антенной системы основано на решении системы связанных интегральных уравнений [1], [2] относительно неизвестных функций распределения токов в вибраторах, однако нередко используется и упрощенный подход – одномодовый метод наведенных э.д.с. [1].
Данную антенную систему можно формально представить как два вибратора, возбуждаемых генераторами с напряжениями 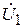 (на активном) и
(на активном) и 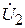 (на пассивном), при этом напряжение второго генератора зависит от тока в нем и сопротивления нагрузки (в данном случае шлейфа регулируемой длины). В этом случае антенная система рассматривается как четырехполюсник, в котором внешнее воздействие задается напряжениями на входах, а реакцией являются входные токи вибраторов
(на пассивном), при этом напряжение второго генератора зависит от тока в нем и сопротивления нагрузки (в данном случае шлейфа регулируемой длины). В этом случае антенная система рассматривается как четырехполюсник, в котором внешнее воздействие задается напряжениями на входах, а реакцией являются входные токи вибраторов 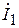 и
и 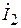 . Токи связаны с напряжениями системой линейных алгебраических уравнений:
. Токи связаны с напряжениями системой линейных алгебраических уравнений:
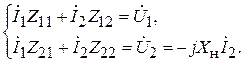 (1.1)
(1.1)
Диагональные элементы матрицы этой системы, т. е. сопротивления 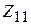 и
и 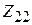 , называются собственными сопротивлениями вибраторов, а
, называются собственными сопротивлениями вибраторов, а 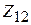 и
и 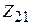 – взаимными сопротивлениями. Ввиду идентичности вибраторов имеет место равенство
– взаимными сопротивлениями. Ввиду идентичности вибраторов имеет место равенство 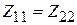 ; ввиду взаимности системы
; ввиду взаимности системы 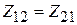 ,
, 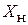 – сопротивление нагрузки (шлейфа). Значения сопротивлений
– сопротивление нагрузки (шлейфа). Значения сопротивлений 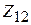 ,
, 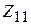 для тонких вибраторов могут быть рассчитаны одномодовым методом наведенных ЭДС в предположении, что токи вдоль вибраторов распределены по закону:
для тонких вибраторов могут быть рассчитаны одномодовым методом наведенных ЭДС в предположении, что токи вдоль вибраторов распределены по закону: 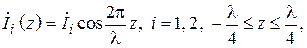 где λ – длина волны в свободном пространстве; z – продольная координата, отсчитываемая от центра каждого вибратора. В этом приближении собственное сопротивление полуволнового вибратора имеет величину
где λ – длина волны в свободном пространстве; z – продольная координата, отсчитываемая от центра каждого вибратора. В этом приближении собственное сопротивление полуволнового вибратора имеет величину 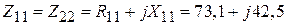 Ом (это значение входного сопротивления соответствует бесконечно тонкому одиночному полуволновому вибратору, для вибратора с отношением длины к толщине равному 60 , более точный подход, основанный на интегральном уравнении, дает другое значение:
Ом (это значение входного сопротивления соответствует бесконечно тонкому одиночному полуволновому вибратору, для вибратора с отношением длины к толщине равному 60 , более точный подход, основанный на интегральном уравнении, дает другое значение: 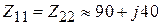 Ом). Взаимное сопротивление
Ом). Взаимное сопротивление 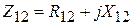 зависит от относительного расстояния между вибраторами d/l. Соответствующие данные для полуволновых вибраторов приведены ниже в таблице. В случае промежуточных расстояний между элементами следует взять соответствующие данные из литературы или провести интерполяцию. График зависимости взаимного импеданса вибраторов в более широком интервале значений нормированного расстояние приведен на рис. 1.4.
зависит от относительного расстояния между вибраторами d/l. Соответствующие данные для полуволновых вибраторов приведены ниже в таблице. В случае промежуточных расстояний между элементами следует взять соответствующие данные из литературы или провести интерполяцию. График зависимости взаимного импеданса вибраторов в более широком интервале значений нормированного расстояние приведен на рис. 1.4.
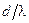
| 0,06 | 0,08 | 0,10 | 0,12 | 0,14 | 0,16 | 0,18 | 0,20 | 0,22 | 0,24 | 0,26 | 0,28 |
| R12 | 71,0 | 69,4 | 67,3 | 64,9 | 62,0 | 58,8 | 55,2 | 51,4 | 47,4 | 43,1 | 38,5 | 34,0 |
| X12 | 20,8 | 14,0 | 7,5 | 1,4 | –4,4 | –9,8 | –14,7 | –19,2 | –23,2 | –26,8 | –29,8 | –32,4 |
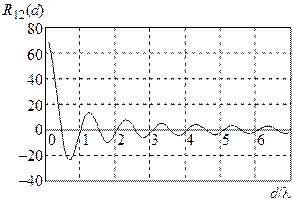
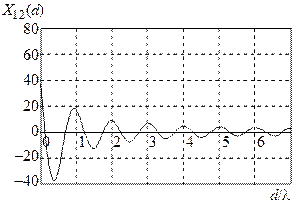
а б
Рис. 1.4
Таким образом, зная геометрию системы (длины вибраторов и расстояние d между ними), определяют элементы ее матрицы сопротивлений, входящие в уравнения (1.1). Решая эти уравнения при известном входном напряжении, находят токи 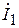 и
и 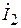 . Далее по этим токам определяют все характеристики антенны – входное сопротивление, диаграмму направленности и т. д. Отношение токов в вибраторах можно непосредственно определить из (1.1):
. Далее по этим токам определяют все характеристики антенны – входное сопротивление, диаграмму направленности и т. д. Отношение токов в вибраторах можно непосредственно определить из (1.1):
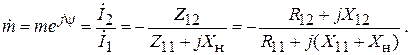 (1.2)
(1.2)
Модуль и фазу этого отношения можно рассчитать по формулам
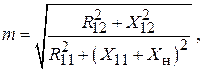 (1.3)
(1.3)
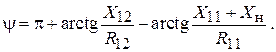 (1.4)
(1.4)
Из системы можно определить также входное сопротивление антенны, т. е. сопротивление, на которое нагружен генератор с напряжением 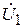 :
:
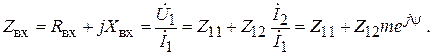 (1.5)
(1.5)
Активная и реактивная части этого сопротивления представляются следующими формулами:
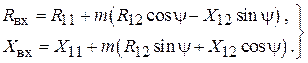 (1.6)
(1.6)
Как видно, входное сопротивление зависит от m и y, а поскольку эти параметры зависят от 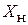 , то, изменяя сопротивление пассивной нагрузки, можно изменять входное сопротивление системы.
, то, изменяя сопротивление пассивной нагрузки, можно изменять входное сопротивление системы.
В данной работе экспериментально снимаются характеристики направленности 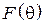 в плоскости, в которой лежат оба вибратора (Е-плоскость). Согласно теореме перемножения ДН, она представляет собой произведение двух сомножителей -
в плоскости, в которой лежат оба вибратора (Е-плоскость). Согласно теореме перемножения ДН, она представляет собой произведение двух сомножителей - 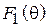 (характеристика направленности одиночного полуволнового вибратора) и
(характеристика направленности одиночного полуволнового вибратора) и 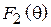 (системный множитель, зависящий от взаимного расположения вибраторов и отношения токов в них):
(системный множитель, зависящий от взаимного расположения вибраторов и отношения токов в них):
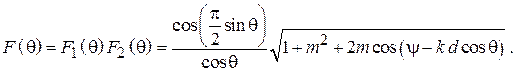 (1.7)
(1.7)
В формуле (1.7) угол отсчитывается от направления, перпендикулярного оси вибраторов (рис.1.3).
Примечание: при расчете по формуле (1.7) следует учитывать появление нуля в знаменателе для углов 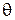 равных +/–90 град.
равных +/–90 град.
Формула (1.7) даeт ненормированную ДН. Нормированная ДН находится по формуле 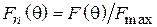 , где
, где 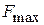 – максимальное значение ДН. Таким образом, расчет диаграммы направленности (ДН) системы при любом значении
– максимальное значение ДН. Таким образом, расчет диаграммы направленности (ДН) системы при любом значении 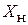 можно произвести по формуле (1.7). Предварительно нужно рассчитать значения
можно произвести по формуле (1.7). Предварительно нужно рассчитать значения 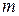 и
и 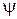 по (1.3) и (1.4).
по (1.3) и (1.4).
Поскольку характеристика направленности (1.7) зависит от параметров 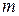 и
и 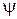 , ясно, что, воздействуя на них путем перестройки нагрузки
, ясно, что, воздействуя на них путем перестройки нагрузки 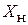 , можно видоизменять (перестраивать) ее форму. В частности, можно обеспечить преимущественное направление излучения под углом
, можно видоизменять (перестраивать) ее форму. В частности, можно обеспечить преимущественное направление излучения под углом 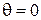 , или под углом
, или под углом 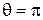 (рис. 1.2). В первом случае пассивный вибратор работает как рефлектор, во втором - как директор. Особенности расчета
(рис. 1.2). В первом случае пассивный вибратор работает как рефлектор, во втором - как директор. Особенности расчета 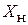 даны в разделе 1.2.
даны в разделе 1.2.
Эффективность пассивного вибратора как рефлектора или директора можно оценить отношением «вперед/назад» 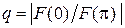 . Если
. Если 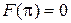 , т. е. излучение «назад» полностью подавлено, то
, т. е. излучение «назад» полностью подавлено, то 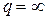 и пассивный вибратор работает как идеальный рефлектор. Если
и пассивный вибратор работает как идеальный рефлектор. Если 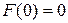 , т. е. полностью подавлено излучение «вперед», то
, т. е. полностью подавлено излучение «вперед», то 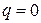 и пассивный вибратор работает как идеальный директор. Для нахождения
и пассивный вибратор работает как идеальный директор. Для нахождения 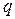 при заданных значениях
при заданных значениях 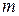 и
и 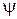 нужно подставить в (1.8)
нужно подставить в (1.8) 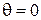 и
и 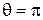 и найти отношение полученных величин:
и найти отношение полученных величин:
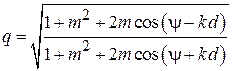 . (1.8)
. (1.8)
1.2. Экспериментальная установка
 Установка состоит из исследуемой двухэлементной вибраторной антенны, один элемент которой (активный) питается от генератора (рабочая частота генератора указана на лабораторном стенде), внутренняя частота модуляции 1 кГц, а второй (пассивный) нагружен на перестраиваемую реактивную нагрузку (отрезок короткозамкнутой экранированной двухпроводной линии). Расстояние между пассивным и активным элементами можно регулировать, его следует установить по указанию преподавателя в интервале от 85 до 190 мм.
Установка состоит из исследуемой двухэлементной вибраторной антенны, один элемент которой (активный) питается от генератора (рабочая частота генератора указана на лабораторном стенде), внутренняя частота модуляции 1 кГц, а второй (пассивный) нагружен на перестраиваемую реактивную нагрузку (отрезок короткозамкнутой экранированной двухпроводной линии). Расстояние между пассивным и активным элементами можно регулировать, его следует установить по указанию преподавателя в интервале от 85 до 190 мм.
На некотором расстоянии от исследуемой антенны установлена приемная антенна, выполненная в виде вибратора со сплошным металлическим рефлектором. В свою очередь, приемная антенна нагружена на амплитудный детектор. Сигнал с выхода детектора подается на селективный низкочастотный измерительный усилитель В6-9, от него по кабелю сигнал передается на рабочее место и регистрируется милливольтметром. Ввиду квадратичности характеристики детектора, сигнал на выходе усилителя пропорционален квадрату диаграммы направленности 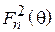 , это следует учесть при обработке результатов эксперимента.
, это следует учесть при обработке результатов эксперимента.
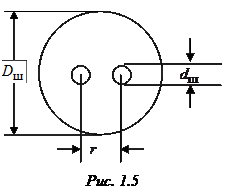
В качестве реактивной нагрузки пассивного вибратора в макете используется шлейф с подвижным короткозамыкателем, выполненный из экранированной двухпроводной линии (поперечное сечение линии приведено на рис. 1.5). Волновое сопротивление шлейфа рассчитывается по формуле[3]:
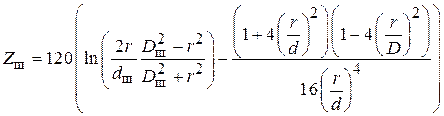 ,
,
где r = 15 мм – расстояние между проводниками двухпроводной линии; 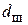 =
=
= 10 мм – диаметр внутренних проводников; 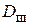 = 36 мм – диаметр экрана.
= 36 мм – диаметр экрана.
Реактивное сопротивление нагрузки 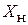 определяется известным выражением из теории длинных линий:
определяется известным выражением из теории длинных линий: 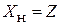 ш
ш 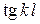 ш, где
ш, где 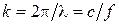 – волновое число;
– волновое число; 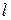 ш – длина шлейфа.
ш – длина шлейфа.
Примечание: для определения истинной длины шлейфа к цифровым значениям на стойке лабораторной установки следует прибавлять величину 50 мм (указана на лабораторном стенде).
1.3. Лабораторный эксперимент
1. Установить расстояние между элементами системы по указанию преподавателя в интервале 85–190 мм (0.12 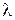 –0.26
–0.26 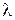 ).
).
2. Убедиться, что установлена частота генератора 417 МГц.
3. Определить экспериментально оптимальную длину шлейфа, соответствующую наилучшему отношению вперед / назад для режима «рефлектора» и (или) «директора» (по указанию преподавателя). Для этого необходимо установить активный элемент в направлении на приемную антенну и снять зависимость уровня сигнала от длины шлейфа реактивной нагрузки пассивного вибратора. Затем, развернув антенную установку в противоположном направлении (пассивным элементом в сторону приемной антенны), снять ту же зависимость. По двум этим зависимостям оперативно рассчитывается отношение вперед / назад 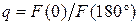 , как функция длины шлейфа и находятся оптимальные длины шлейфа, соответствующие максимальному (больше единицы) и минимальному значениям параметра q.
, как функция длины шлейфа и находятся оптимальные длины шлейфа, соответствующие максимальному (больше единицы) и минимальному значениям параметра q.
4. Снять диаграммы направленности 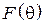 антенной системы в режимах директора и рефлектора, установив длины шлейфа, найденные из предыдущего эксперимента. Шаг измерения угла q – 10º в пределах 0...360º.
антенной системы в режимах директора и рефлектора, установив длины шлейфа, найденные из предыдущего эксперимента. Шаг измерения угла q – 10º в пределах 0...360º.
1.4. Контрольные вопросы
1. Как объяснить физически преимущественное излучение системы из двух параллельных вибраторов при их настройке в режиме рефлектора или директора?
2. Прокомментируйте назначение всех элементов лабораторной установки.
3. Дайте определение директора и рефлектора.
4. Оцените коэффициент направленного действия (КНД) системы из двух вибраторов по сравнению с одиночным вибратором.
5. Нарисуйте на одном графике нормированную ДН одного вибратора и ДН системы в режиме директора и рефлектора.
6. Сравните фазу и амплитуду тока в активном и пассивном вибраторе.
7. Какие элементы Z-матрицы системы (1.1) учитывают влияние вибраторов друг на друга?
8. Как ведут себя сопротивления 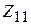 и
и 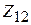 при увеличении расстояния между вибраторами?
при увеличении расстояния между вибраторами?
9. Изобразите функцию распределения тока вдоль полуволнового вибратора.
10. Чему равно входное сопротивление одиночного полуволнового вибратора?
11. Известно расстояние между полуволновыми вибраторами в долях длины волны. Откуда можно извлечь информацию об их взаимном сопротивлении?
12. Почему в качестве нагрузки пассивного вибратора используется реактивное сопротивление (а не активное или комплексное с ненулевой вещественной частью)?
13. За счет чего возникает напряжение в центре пассивного вибратора?
14. Как будут выглядеть уравнения (1.1), если вход пассивного вибратора замкнуть накоротко?
15. Опираясь на выражение (1.2), выведите выражения (1.3) и (1.4).
16. Что понимают под входным сопротивлением антенны, состоящей из активного и пассивного вибраторов?
17. Опираясь на выражение (1.5), выведите выражения (1.6).
18. От каких параметров зависит системный множитель ДН рассматриваемой антенны?
19. Покажите на формулах, что характеристику направленности системы можно изменять, перестраивая сопротивление 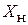 .
.
20. Что такое отношение «вперед/назад»?
21. В каких случаях можно говорить, что пассивный вибратор работает как идеальный рефлектор или директор? Чему в этих случаях равно отношение q?
1.5. Содержание отчета
Отчет должен содержать:
1. Структурную схему установки с указанием всех основных узлов приемного и передающего тракта;
2. Результаты эксперимента в виде зависимостей уровня поля от длины шлейфа, ДН в режиме рефлектора и директора с указанием расстояния между элементами и выбранных оптимальных значений длин шлейфа;
3. Расчетные данные:
– график отношения вперед/назад (1.9), как функция длины шлейфа. Здесь следует отметить, что коэффициент m (отношение токов в вибраторах) зависит от Хн, который в свою очередь определяется длинной шлейфа lш.
– расчетные ДН в виде графиков (1.8).
4. Выводы по работе.
2. ИССЛЕДОВАНИЕ СПИРАЛЬНОЙ АНТЕННЫ
2.1. Введение. Теоретические сведения
Спиральные антенны (СА) широко используются в качестве самостоятельных излучателей или в составе небольших антенных решеток как широкополосные излучатели круговой поляризации, работающие в режиме осевого излучения. Чаще всего СА представляет собой спиральный проводник ограниченной длины (несколько длин волн), намотанный на диэлектрический каркас, один конец проводника СА подсоединен к внутренней жиле возбуждающего коаксиального кабеля, другой оставлен свободным. Внешняя оплетка кабеля присоединяется к проводящему экрану (основанию) (рис. 2.1). Наиболее распространен режим работы цилиндрической СА, при котором диаметр цилиндра равен одной трети длины волны, при этом периметр витка спирали около одной длины волны. Именно в этом случае имеет место режим осевого излучения с круговой поляризацией. Различают цилиндрические и конические спирали, последние характеризуются большей полосой частот. В данной работе исследуются две цилиндрические СА с экраном, оптимизированные под диапазон частот 1.7–2.7 ГГц (НЧ спиральная антенна) и 2.5–4 ГГц (ВЧ антенна). Экспериментальные частотные зависимости коэффициента отражения в тракте питания этих антенн приведены на рис. 2.2.
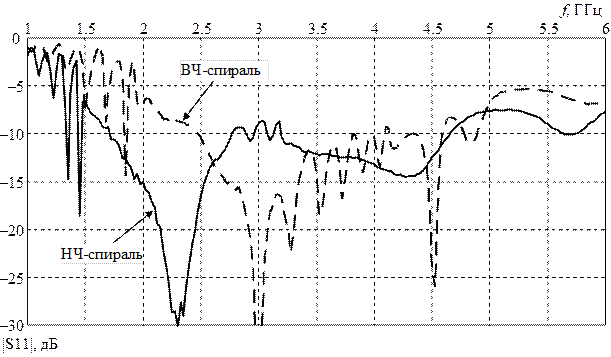
Рис. 2.2
 На рис. 2.3 показаны качественно диаграммы направленности СА в полосе частот. Основным рабочим диапазоном СА считается интервал 0,7 <
На рис. 2.3 показаны качественно диаграммы направленности СА в полосе частот. Основным рабочим диапазоном СА считается интервал 0,7 < 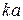 < 1,3, в котором она имеет осевое излучение и круговую поляризацию (
< 1,3, в котором она имеет осевое излучение и круговую поляризацию ( 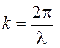 – волновое число,
– волновое число, 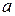 – радиус). При
– радиус). При 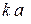 << 1 ДН спиральной антенны близка по форме к ДН диполя Герца, а при
<< 1 ДН спиральной антенны близка по форме к ДН диполя Герца, а при 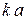 >> 1 она имеет воронкообразный характер.
>> 1 она имеет воронкообразный характер.
Геометрия цилиндрической СА приведена на рис. 2.4. Здесь введены следующие обозначения: 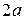 – диаметр СА;
– диаметр СА; 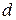 – шаг витка спирали;
– шаг витка спирали; 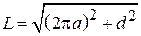 – длина витка спирали;
– длина витка спирали; 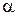 – угол подъема витка спирали, град. (обычно выбирают
– угол подъема витка спирали, град. (обычно выбирают 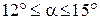 );
); 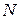 – число витков.
– число витков.
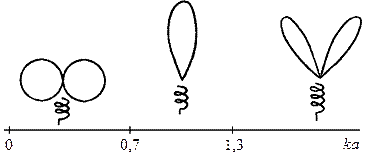
Рис. 2.3
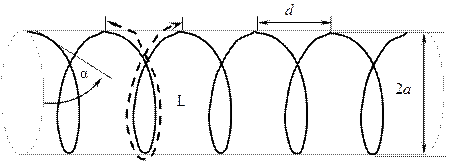
Рис. 2.4
Рис. 2.5 поясняет механизм формирования поля круговой поляризации в режиме осевого излучения СА. При длине витка СА, близкому к длине волны, в антенне устанавливается режим бегущей волны тока и в каждый момент времени одному витку СА можно поставить в соответствие два одина-
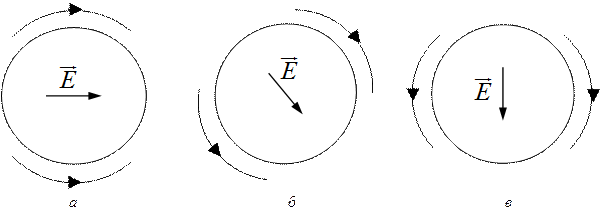
Рис. 2.5
ковых синфазных изогнутых диполя. В частности, на рис. 2.5, а, б, в последовательно, в трех разных моментах времени виток эквивалентен двум изогнутым диполям, принимающим различные угловые положения в плоскости витка. Результирующий вектор напряженности излученного электрического поля вращается с постоянной длиной.
ДН спиральной антенны как ДН антенной решетки, состоящей из кольцевых плоских излучателей. Для приближенного расчета диаграммы направленности СА ее удобно рассматривать как систему, состоящую из N одинаковых элементов, расположенных вдоль продольной оси z с шагом d. Такая система носит название одномерной (линейной) антенной решетки. Ее элементами в данном случае являются неплоские витки спирали. Они возбуждены со сдвигом фаз от витка к витку 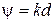 . В соответствии с теоремой перемножения диаграмм направленности ДН такой антенной решетки представляет собой произведение множителя решетки (системного множителя)
. В соответствии с теоремой перемножения диаграмм направленности ДН такой антенной решетки представляет собой произведение множителя решетки (системного множителя) 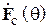 и характеристики направленности ее элемента – в данном случае витка спирали
и характеристики направленности ее элемента – в данном случае витка спирали 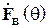 :
:
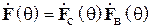 . (2.1)
. (2.1)
Системный множитель. В общем случае, когда в решетке скачок фазы  между соседними элементами имеет произвольное значение, модуль системного множителя, входящего в (2.1), представляется выражением
между соседними элементами имеет произвольное значение, модуль системного множителя, входящего в (2.1), представляется выражением
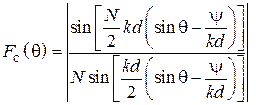 . (2.2)
. (2.2)
В нашем случае 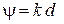 и входящее в (2.2) отношение
и входящее в (2.2) отношение 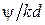 равно единице, с учетом этого:
равно единице, с учетом этого:
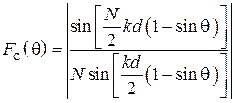 .
.
Диаграммы направленности витка спирали. Характеристика направленности такого витка известна из теории антенн, она имеет две составляющие – по ортам сферической системы координат 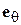 и
и 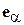 [4], [5] (рис. 2.6):
[4], [5] (рис. 2.6):
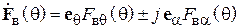 , (2.3)
, (2.3)
где
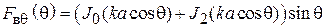 (2.4)
(2.4)
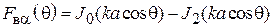 , (2.5)
, (2.5)
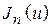 – функция Бесселя n-го порядка,
– функция Бесселя n-го порядка, 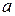 – радиус витка спирали. В формулах (2.4), (2.5) учтено, что осевое направление в данном лабораторном макете соответствует углу
– радиус витка спирали. В формулах (2.4), (2.5) учтено, что осевое направление в данном лабораторном макете соответствует углу 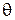 равному 90 градусов. В выражении (2.3) знак перед вторым слагаемым зависит от того, в какую сторону выполнена намотка спирали. Как видно из (2.3), q-я и j-я составляющие характеристики направленности сдвинуты на 90о по фазе. Следовательно, вектор
равному 90 градусов. В выражении (2.3) знак перед вторым слагаемым зависит от того, в какую сторону выполнена намотка спирали. Как видно из (2.3), q-я и j-я составляющие характеристики направленности сдвинуты на 90о по фазе. Следовательно, вектор 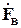 является эллиптически поляризованным, как и векторы напряженности электрического и магнитного полей. В направлении нормали к плоскости витка (осевом), т. е. при
является эллиптически поляризованным, как и векторы напряженности электрического и магнитного полей. В направлении нормали к плоскости витка (осевом), т. е. при 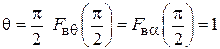 , таким образом, в этом направлении поле излучения имеет круговую поляризацию.
, таким образом, в этом направлении поле излучения имеет круговую поляризацию.
КНД и ширина главного лепестка диаграммы направленности. Для приближенного расчета параметров ДН спиральных антенн полезны следующие полуэмпирические формулы [1], [2]. Ширина главного лепестка ДН по уровню половинной мощности (град.):
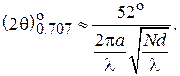 (2.6)
(2.6)
Коэффициент направленного действия цилиндрической СА
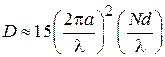 . (2.7)
. (2.7)
2.2. Экспериментальная установка
В экспериментальной установке имеются две спиральные антенны разного диаметра. Геометрические параметры антенн приведены ниже.
Для низкочастотной (т. е. для антенны большего диаметра):
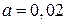 м – радиус спирали;
м – радиус спирали;
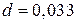 м – шаг намотки спирали;
м – шаг намотки спирали;
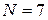 – число витков.
– число витков.
Для высокочастотной СА (т. е. для антенны меньшего диаметра):
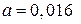 м – радиус спирали;
м – радиус спирали;
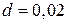 м – шаг намотки спирали;
м – шаг намотки спирали;
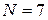 – число витков.
– число витков.
Обе антенны подключаются к генератору Г4-194 и работают как передающие. Положение органов управления генератора Г4-194 перед началом работы:
· сеть – включено;
· перестройка частоты – ручная;
· фильтр – включен;
· модуляция – внутренняя;
· СВЧ – включено;
· ручка АРМ/уровень – в среднее положение.
Частота генератора устанавливается по указанию преподавателя для каждой антенны.
В качестве приемной используется рупорная антенна с переходом в П-образный волновод для обеспечения возможности работы установки в широкой полосе рабочих частот. Принимаемый сигнал демодулируется квадратичным детектором, сигнал с выхода детектора подается на измерительный усилитель.
Угол подъема витков в обеих спиралях близок к оптимальному, таким образом, рабочий диапазон частот в обоих случаях является максимально возможным. Для низкочастотной антенны он равен 1,7...2,7 ГГц, для высокочастотной антенны он равен 2,5...4,0 ГГц (по критерию уровня коэффициента отражения не хуже минус 10 дБ).
Измерение диаграмм направленности осуществляется за счет вращения исследуемых спиральных антенн вокруг вертикальной оси. При этом имеется возможность менять ориентацию плоскости поляризации приемной рупорной антенны. Для каждой СА снимается ДН с вертикальной и горизонтальной поляризацией приемного рупора относительно плоскости стола.
2.3. Проведение измерений
1. Установить исследуемую СА на поворотное устройство. Настроить генератор, питающий рупорную антенну, на частоту 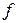 , заданную преподавателем. Снять диаграммы направленности спиральной антенны
, заданную преподавателем. Снять диаграммы направленности спиральной антенны 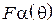 (приемная рупорная антенна в этом случае устанавливается с вертикальной ориентацией вектора Е) и
(приемная рупорная антенна в этом случае устанавливается с вертикальной ориентацией вектора Е) и 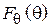 (приемный рупор имеет горизонтальную поляризацию).
(приемный рупор имеет горизонтальную поляризацию).
2. Повторить п. 1 для второй СА.
Примечание: при обработке данных эксперимента следует учесть, что детектор в индикаторной части макета имеет квадратичную характеристику
2.4. Контрольные вопросы
1. Перечислите основные особенности спиральных антенн.
2. Какова зависимость формы ДН спиральных антенн от длины волны?
3. При каких условиях в спиральной антенне возможно излучение поля круговой поляризации?
4. Объясните физически возможность появление круговой поляризации в поле излучения СА.
5. Дайте физическую трактовку форме ДН СА для малого электрического радиуса.
6. Какому режиму соответствует работа малогабаритной рамочной антенны средневолнового приемника?
7. Что такое круговая поляризация?
8. Какими свойствами обладает спираль, если ее электрический радиус находится в пределах 0,7 < 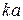 < 1,3?
< 1,3?
9. Каким принимается распределение тока в приближенной теории спиральных антенн? Какими обстоятельствами при этом пренебрегают?
10. Как представляется в теории антенных решеток характеристика направленности?
11. Из какого выражения в тексте следует, что поле излучения витка антенны является эллиптически поляризованным? Как аргументируется это утверждение?
12. Опишите процедуру экспериментального снятия диаграмм направленности 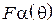 и
и 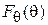 .
.
13. От каких параметров зависят направленные свойства СА в режиме осевого излучения?
14. Как зависит ширина главного лепестка ДН СА с увеличением числа витков?
15. Какова геометрия СА с умеренной направленностью и круговой поляризацией для диапазона метровых волн?
2.5. Содержание отчета
Отчет должен содержать:
1. Цель работы, блок-схему установки.
2. Таблицы экспериментальных данных.
3. Основные расчетные формулы. Рассчитанные и экспериментально снятые ДН спиральных антенн в полярной или декартовой системе координат, представленные на одном рисунке.
4. Результаты расчетов ширины главного лепестка и КНД СА по формулам (2.6), (2.7) (КНД рассчитать в децибеллах и относительных единицах).
5. Выводы по работе.
3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ
РУПОРНОЙ АНТЕННЫ
3.1. Теоретические сведения
Все параметры, характеризующие антенны, можно разделить на 2 группы. К первой группе следует отнести параметры, характеризующие антенну как элемент цепи приёмопередающего тракта. Так, передающая антенна может рассматриваться как нагрузка для выходного каскада передатчика и описываться соответствующими параметрами теории цепей: входным сопротивлением, коэффициентом отражения и т. д. Приёмная антенна с этой точки зрения может рассматриваться как обладающий определённым внутренним сопротивлением источник напряжения.
Ко второй группе следует отнести параметры, характеризующие антенну как элемент, преобразующий энергию, поступающую по фидерному тракту, в энергию электромагнитных волн, распространяющихся в пространстве, и распределяющий в пространстве интенсивность полей этих волн (передающая антенна). Приёмная же антенна может рассматриваться как устройство, преобразующее энергию пространственных электромагнитных волн (с учётом направления их прихода) в энергию волн фидера. В эту группу включены такие параметры и характеристики, как коэффициент полезного действия (КПД), диаграмма направленности (ДН), коэффициент направленного действия (КНД), коэффициент усиления (КУ) и др.
Как правило, в реальных антеннах всегда имеются необратимые потери энергии, связанные, в основном, с конечным значением проводимости металла и неидеальностью диэлектрика. Из-за этого мощность 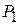 , преобразованная антенной, всегда будет меньше мощности
, преобразованная антенной, всегда будет меньше мощности 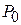 , поступающей в антенну. КПД антенны
, поступающей в антенну. КПД антенны 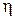 характеризует эффективность преобразования энергии и определяется соотношением
характеризует эффективность преобразования энергии и определяется соотношением 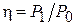 .
.
Другие параметры второй группы, упомянутые здесь, определяются для дальней зоны антенны.
В дальней зоне (зоне излучения) электромагнитное поле, созданное антенной, представляет собой поперечную волну со сферическим волновым фронтом. Дальняя зона формируется при удалении от антенны на расстояние R, удовлетворяющее следующим условиям:
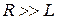 , R >> l,
, R >> l, 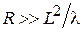 , (3.1)
, (3.1)
где L – максимальный линейный размер апертуры антенны; l – рабочая длина волны.
ДН описывает пространственное распределение амплитуды поля излучения антенны в дальней зоне.
КНД антенны D характеризует степень концентрации антенного излучения в заданном направлении (обычно в направлении максимального излучения). По определению, значение коэффициента направленного действия показывает, во сколько раз плотность потока мощности излучения рассматриваемой антенны в заданном направлении больше плотности потока мощности, создаваемого изотропным (ненаправленным) излучателем при условии равенства полных мощностей, излучаемых рассматриваемой и изотропной антеннами. Как показано в теории антенн, КНД апертурной антенны с синфазным раскрывом можно найти по формуле
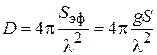 , (3.2)
, (3.2)
где 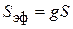 – эффективная площадь апертуры; S – её геометрическая площадь; g – апертурный коэффициент использования поверхности раскрыва (КИП), связанный с распределением по апертуре касательной составляющей поля
– эффективная площадь апертуры; S – её геометрическая площадь; g – апертурный коэффициент использования поверхности раскрыва (КИП), связанный с распределением по апертуре касательной составляющей поля 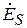 следующим соотношением:
следующим соотношением:
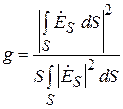 .
.
КУ антенны G показывает, во сколько раз плотность потока мощности излучения антенны в заданном направлении больше плотности потока мощности, создаваемого идеальным (без потерь) изотропным излучателем при условии равенства мощностей, подводимых к рассматриваемой и изотропной антеннам. Из определения видно, что КУ антенны характеризует степень концентрации излучения в пространстве с учётом потерь в антенне. Между КУ и КНД существует связь: G = Dh.
На практике нередко значения КНД или КУ определяют в децибелах (дБ). Коэффициент усиления G1 (в дБ) связан с величиной G, выраженной в относительных единицах, равенством G1 = 10 lg G .
В данной работе производятся измерения коэффициентов усиления рупорных антенн.
Рупорная антенна состоит из отрезка волновода постоянного сечения размером 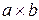 и собственно рупора, представляющего собой волновод с плавно изменяющимся сечением, с размерами раскрыва
и собственно рупора, представляющего собой волновод с плавно изменяющимся сечением, с размерами раскрыва 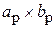 . На практике применяются 2 типа прямоугольных рупоров – секториальные и пирамидальные. Секториальными называются рупоры, у которых расширяется только одна пара стенок. В зависимости от того, в какой плоскости происходит расширение, различают Е-плоскостные (
. На практике применяются 2 типа прямоугольных рупоров – секториальные и пирамидальные. Секториальными называются рупоры, у которых расширяется только одна пара стенок. В зависимости от того, в какой плоскости происходит расширение, различают Е-плоскостные ( 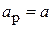 ,
, 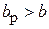 ) и Н-плоскостные (
) и Н-плоскостные ( 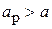 ,
, 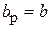 ) рупоры. Пирамидальными называются рупоры, расширяющиеся как в плоскости вектора Е, так и в плоскости вектора Н.
) рупоры. Пирамидальными называются рупоры, расширяющиеся как в плоскости вектора Е, так и в плоскости вектора Н.
Характеристики излучения рупорной антенны определяются структурой поля в ее раскрыве. В общем случае ДН 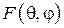 плоской прямоугольной излучающей апертуры размером
плоской прямоугольной излучающей апертуры размером 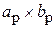 описывается выражением
описывается выражением
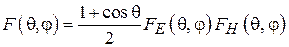 . (3.3)
. (3.3)
Функции 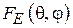 и
и 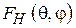 определяются амплитудно-фазовым распределением поля в раскрыве апертуры в плоскостях векторов E и H соответственно.
определяются амплитудно-фазовым распределением поля в раскрыве апертуры в плоскостях векторов E и H соответственно.
Для рупорной антенны с достаточной точностью можно считать, что амплитуда поля в раскрыве распределена так же, как и амплитуда поля основной волны прямоугольного волновода 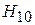 , т. е. имеет косинусоидальное распределение вдоль оси x и равномерное вдоль оси y:
, т. е. имеет косинусоидальное распределение вдоль оси x и равномерное вдоль оси y:
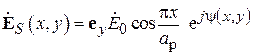 .
.
В случае синфазного раскрыва (y(x, y) = const) функции 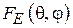 и
и 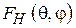 будут определяться формулами
будут определяться формулами
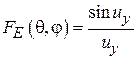 ,
, 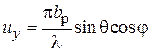 , (3.4)
, (3.4)
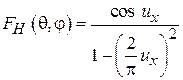 ,
, 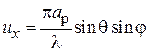 . (3.5)
. (3.5)
Значение КИП для синфазной апертуры с таким амплитудным распределением g = 0,81.
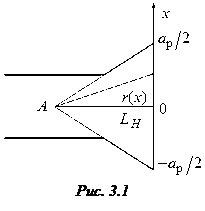 Фазовое распределение в апертуре реальной рупорной антенны будет отлично от равномерного. Рассмотрим причину несинфазности раскрыва на примере Н-плоскостного рупора (рис. 3.1). Волна
Фазовое распределение в апертуре реальной рупорной антенны будет отлично от равномерного. Рассмотрим причину несинфазности раскрыва на примере Н-плоскостного рупора (рис. 3.1). Волна 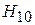 питающего волновода, переходя в рупор, трансформируется в волну с цилиндрическим фазовым фронтом, которая как бы исходит из линейного источника A, находящегося на пересечении продолжений граней рупора. Если приближенно считать, что цилиндрическая волна распространяется между параллельными широкими стенками рупора с волновым числом k, то набег фазы в точке апертуры с координатой x равен kr(x), а в центре апертуры –
питающего волновода, переходя в рупор, трансформируется в волну с цилиндрическим фазовым фронтом, которая как бы исходит из линейного источника A, находящегося на пересечении продолжений граней рупора. Если приближенно считать, что цилиндрическая волна распространяется между параллельными широкими стенками рупора с волновым числом k, то набег фазы в точке апертуры с координатой x равен kr(x), а в центре апертуры – 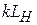 (
( 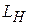 – длина Н-плоскостного рупора). Таким образом, разность фаз в точках с координатами x и 0
– длина Н-плоскостного рупора). Таким образом, разность фаз в точках с координатами x и 0
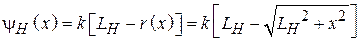 .
.
Предполагая, что угол раскрыва рупора мал, заменим корень в этом выражении первыми двумя членами разложения Маклорена:
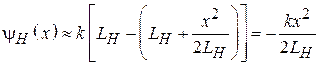 . (3.6)
. (3.6)
Отсюда видно, что расфазировка возрастает от центра к краю апертуры приблизительно по квадратичному закону и максимальное её значение – фазовая ошибка 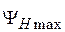 – достигается на краю раскрыва:
– достигается на краю раскрыва:
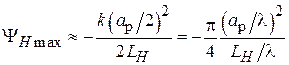 . (3.7)
. (3.7)
Диаграмма направленности Н-плоскостного рупора с фазовым распределением (3.6) описывается формулой (3.3), где 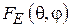 определяется выражением (3.4), а
определяется выражением (3.4), а 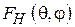 при условии малости угла раскрыва рупора даётся интегралом
при условии малости угла раскрыва рупора даётся интегралом
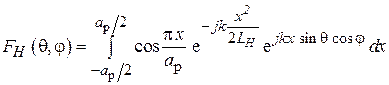 ,
,
который может быть представлен линейной комбинацией специальных функций – интегралов Френеля [6].
На рис. 3.2 представлены диаграммы направленности 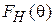 в плоскости Н (j = 0) для рупора с размером
в плоскости Н (j = 0) для рупора с размером 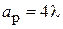 при различных значениях нормированной длины рупора
при различных значениях нормированной длины рупора 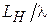 и, согласно (3.7), максимальной фазовой ошибки
и, согласно (3.7), максимальной фазовой ошибки 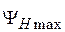 . Кривая 2 соответствует значению
. Кривая 2 соответствует значению 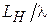 = 20, кривая 3 –
= 20, кривая 3 – 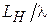 = 10, 4 –
= 10, 4 – 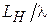 = 5. Для сравнения там же приведена диаграмма направленности синфазного раскрыва (кривая 1). Как видно из графиков, наличие в раскрыве квадратичной фазовой ошибки (3.6) приводит к деформации ДН: заплывают нули, увеличивается уровень бокового излучения, расширяется основной лепесток.
= 5. Для сравнения там же приведена диаграмма направленности синфазного раскрыва (кривая 1). Как видно из графиков, наличие в раскрыве квадратичной фазовой ошибки (3.6) приводит к деформации ДН: заплывают нули, увеличивается уровень бокового излучения, расширяется основной лепесток.
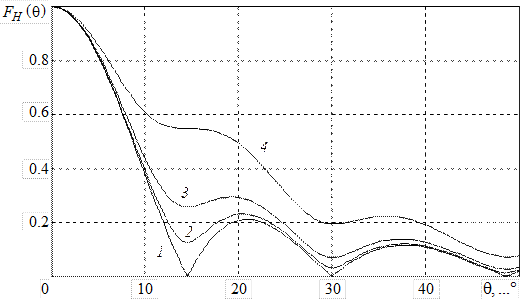
Рис. 3.2
Аналогичным образом влияет на диаграмму направленности в плоскости Е ( 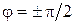 ) для Е-плоскостного рупора фазовая ошибка
) для Е-плоскостного рупора фазовая ошибка 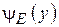 , определяемая выражением
, определяемая выражением
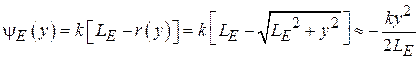 .
.
В этом случае для расчёта диаграммы направленности рупора в формулу (3.3) следует подставить 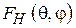 из (3.5), а
из (3.5), а 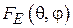 будет выражаться интегралом
будет выражаться интегралом
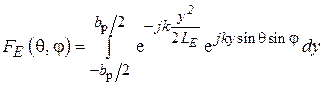 ,
,
также сводимым к линейной комбинации интегралов Френеля.
Влияние фазовой ошибки в раскрыве рупорной антенны проявляется в том, что значение КИП зависит от относительных размеров рупора 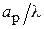 ,
, 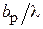 ,
, 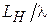 ,
, 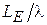 . Таким образом, КНД Н-плоскостного рупора будет определяться выражением
. Таким образом, КНД Н-плоскостного рупора будет определяться выражением
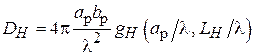 ,
,
где 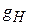 – функция, определяющая зависимость КИП (g) от комбинации параметров
– функция, определяющая зависимость КИП (g) от комбинации параметров 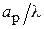 и
и 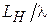 . Пользуясь общим выражением для КИП, нетрудно показать, что
. Пользуясь общим выражением для КИП, нетрудно показать, что
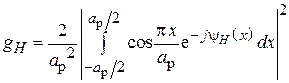 .
.
Удобнее, однако, иметь дело с приведённым КНД 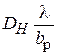 , поскольку при варьировании размеров Н-плоскостного рупора отношение
, поскольку при варьировании размеров Н-плоскостного рупора отношение 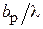 остаётся неизменным. Очевидно, приведённый КНД Н-плоскостного рупора будет определяться выражением
остаётся неизменным. Очевидно, приведённый КНД Н-плоскостного рупора будет определяться выражением
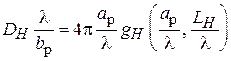 .
.
Аналогичным образом можно найти и приведённый КНД для Е-плоскостного рупора:
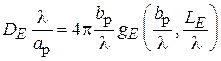 ,
,
где
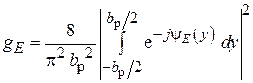 .
.
На рис. 3.3 и 3.4 изображены графики зависимостей приведённых КНД 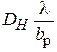 и
и 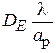 от нормированных размеров раскрыва
от нормированных размеров раскрыва 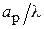 и
и 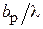 для H- и E-плоскостных рупоров соответственно. Параметры
для H- и E-плоскостных рупоров соответственно. Параметры 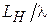 на рис. 3.3 и
на рис. 3.3 и 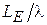 на рис. 3.4 принимают значения от 2 (кривая 1) до 6 (кривая 11) с шагом 0,4. Как видно из этих графиков, с увеличением относительных размеров раскрыва рупора (
на рис. 3.4 принимают значения от 2 (кривая 1) до 6 (кривая 11) с шагом 0,4. Как видно из этих графиков, с увеличением относительных размеров раскрыва рупора ( 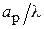 или
или 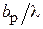 ) при его неизменной длине
) при его неизменной длине 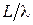 КНД сначала возрастает, так как увеличиваются размеры излучающей поверхности, которая остаётся практически синфазной (сдвиг фаз
КНД сначала возрастает, так как увеличиваются размеры излучающей поверхности, которая остаётся практически синфазной (сдвиг фаз 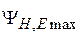 мал). При этом ДН становится уже. При дальнейшем увеличении размеров раскрыва заметно растут фазовые искажения, что приводит к снижению КНД и расширению ДН.
мал). При этом ДН становится уже. При дальнейшем увеличении размеров раскрыва заметно растут фазовые искажения, что приводит к снижению КНД и расширению ДН.
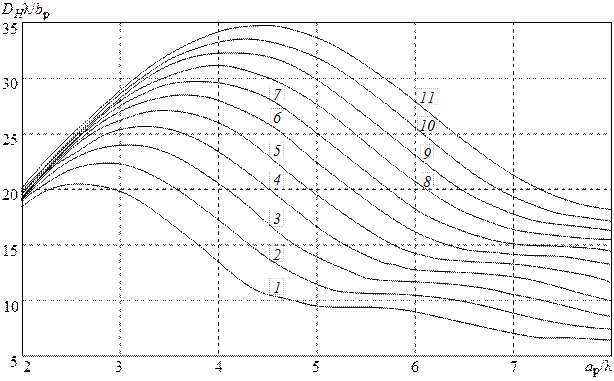
Рис. 3.3
Допустимое значение максимальной фазовой ошибки 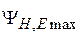 определяется условием получения наибольшего КНД при заданной относительной длине
определяется условием получения наибольшего КНД при заданной относительной длине 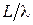 рупора. Установлено, что в случае Е-плоскостного рупора максимальный КНД получается при выполнении соотношения
рупора. Установлено, что в случае Е-плоскостного рупора максимальный КНД получается при выполнении соотношения 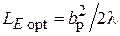 , что
, что
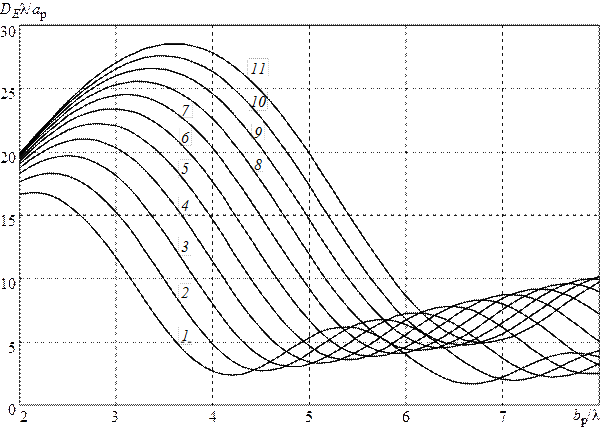
Рис. 3.4
соответствует максимальной допустимой фазовой ошибке 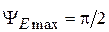 . Оптимальная длина и максимальная допустимая фазовая ошибка Н-плоскостного рупора определяются, соответственно, выражениями
. Оптимальная длина и максимальная допустимая фазовая ошибка Н-плоскостного рупора определяются, соответственно, выражениями 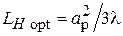 и
и 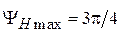 .
.
Увеличение допустимого сдвига фаз в апертуре Н-плоскостного рупора по сравнению с Е-плоскостным объясняется спаданием амплитуды возбуждающего поля к краям этого рупора.
Следует отметить, что «оптимальность» здесь понимается в смысле получения наибольшего значения КНД при заданной длине рупора 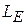 или
или 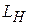 .
.
Коэффициент направленного действия оптимального Е- или Н-плоскостного рупора
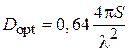 .
.
КНД пирамидального рупора с размерами раскрыва 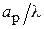 и
и 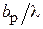 можно рассчитать по формуле
можно рассчитать по формуле
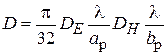 , (3.8)
, (3.8)
где приведённые значения КНД для секториальных рупоров 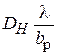 и
и 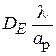 могут быть определены по графикам на рис. 3.3 и 3.4.
могут быть определены по графикам на рис. 3.3 и 3.4.
3.2. Методика измерения коэффициента усиления антенны
Метод, используемый для измерения коэффициента усиления рупорной антенны, основан на следующей модели. Предположим, имеются 2 идентичные антенны, разнесённые на расстояние 2R, которое удовлетворяет условию дальней зоны (3.1). Пусть при этом направление максимального излучения антенн совпадает с осевой линией системы (рис. 3.5). Очевидно, систему можно
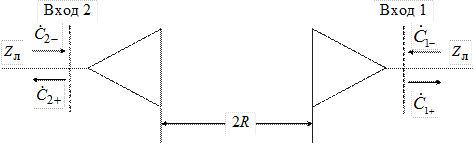
Рис. 3.5
рассматривать как волновой четырёхполюсник, который описывается матрицей рассеяния, причём ввиду симметрии системы между элементами матрицы имеются очевидные связи: 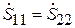 ,
, 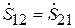 . Следовательно, амплитуды падающих и расходящихся волн на входах 1 и 2 связаны соотношениями
. Следовательно, амплитуды падающих и расходящихся волн на входах 1 и 2 связаны соотношениями
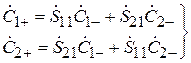 . (3.9)
. (3.9)
Элементы S-матрицы однозначно связаны с параметрами антенн и геометрией системы в целом. Для выяснения этих связей поставим систему в испытательный режим, при котором на вход 1 поступает падающая волна с комплексной амплитудой 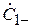 , несущая мощность
, несущая мощность 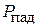 , а вход 2 нагружен на согласованную нагрузку
, а вход 2 нагружен на согласованную нагрузку 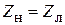 (рис. 3.6). В этом случае
(рис. 3.6). В этом случае 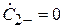 и система (3.9) принимает вид
и система (3.9) принимает вид
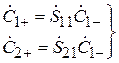 .
.
Приведенные условия работы системы отображены на рис. 3.6.
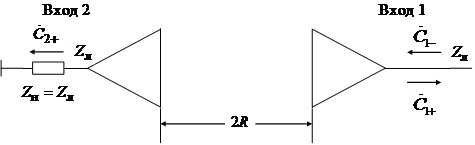
Рис. 3.6
Мощность, излучаемая первой антенной с учётом её КПД h, 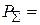
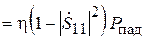 , а плотность потока мощности, падающей на апертуру второй антенны:
, а плотность потока мощности, падающей на апертуру второй антенны:
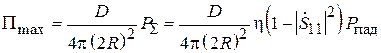 . (3.10)
. (3.10)
Антенна 2 в данном случае работает как приёмная и мощность 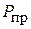 , принимаемая ею, определяется выражением
, принимаемая ею, определяется выражением 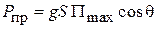 , где
, где 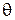 – угол между нормалью к апертуре приёмной антенны и направлением на антенну передающую (в данном случае
– угол между нормалью к апертуре приёмной антенны и направлением на антенну передающую (в данном случае 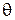 = 0). В свою очередь, часть мощности
= 0). В свою очередь, часть мощности 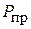 переизлучается в окружающее пространство, а часть поступает в согласованную нагрузку. Мощность, поглощаемую в нагрузке приёмной антенны, можно рассчитать по формуле
переизлучается в окружающее пространство, а часть поступает в согласованную нагрузку. Мощность, поглощаемую в нагрузке приёмной антенны, можно рассчитать по формуле
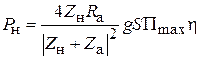 ,
,
где 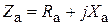 – сопротивление излучения антенны.
– сопротивление излучения антенны.
Первый множитель в последнем равенстве равен  , где
, где 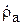 – коэффициент отражения в линии с волновым сопротивлением
– коэффициент отражения в линии с волновым сопротивлением 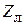 , нагруженной на сопротивление
, нагруженной на сопротивление 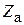 . Учитывая (3.10), получим
. Учитывая (3.10), получим
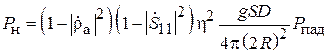 .
.
Выражая далее gS через D и l из (3.2) и учитывая, что hD = G, найдём
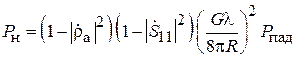 .
.
Множитель перед 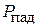 представляет собой коэффициент прохождения мощности из линии 1 в линию 2, т. е. квадрат модуля элемента
представляет собой коэффициент прохождения мощности из линии 1 в линию 2, т. е. квадрат модуля элемента 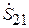 , так что
, так что
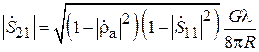 . (3.11)
. (3.11)
Фаза элемента 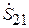 зависит, очевидно, от электрического расстояния между антеннами и может быть представлена как
зависит, очевидно, от электрического расстояния между антеннами и может быть представлена как 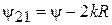 , так что
, так что
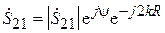 . (3.12)
. (3.12)
Перейдём к элементу 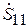 S-матрицы рассматриваемой системы. Он имеет смысл коэффициента отражения на входе 1 в рассматриваемом испытательном режиме:
S-матрицы рассматриваемой системы. Он имеет смысл коэффициента отражения на входе 1 в рассматриваемом испытательном режиме: 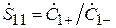 . Но в линии 1 отражённая волна порождается двумя причинами: а) неидеальным согласованием антенны с линией, что в режиме излучения в свободное пространство было учтено коэффициентом отражения
. Но в линии 1 отражённая волна порождается двумя причинами: а) неидеальным согласованием антенны с линией, что в режиме излучения в свободное пространство было учтено коэффициентом отражения 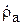 , и б) вторичным излучением антенны 2, которое принимается антенной 1. В связи с этим в линии 1 появляется «добавочная» отражённая волна с амплитудой
, и б) вторичным излучением антенны 2, которое принимается антенной 1. В связи с этим в линии 1 появляется «добавочная» отражённая волна с амплитудой 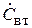 . Таким образом,
. Таким образом, 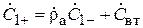 , откуда
, откуда 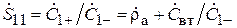 .
.
Можно показать, что, поскольку антенны расположены на расстоянии, соответствующем дальней зоне, второе слагаемое в этом выражении будет существенно меньше первого (на один–два порядка) и им вполне можно пренебречь. Поэтому можно считать 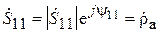 . Теперь выражение (3.11) можно переписать в виде
. Теперь выражение (3.11) можно переписать в виде
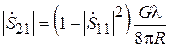 , (3.13)
, (3.13)
откуда
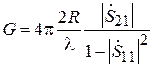 . (3.14)
. (3.14)
Таким образом, установлена связь между элементами S-матрицы и параметрами антенны.
Поставим теперь рассматриваемую систему в режим противофазного возбуждения, когда 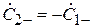 . В этом случае, в соответствии с (3.9),
. В этом случае, в соответствии с (3.9), 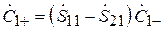 , т. е. коэффициент отражения на входе 1
, т. е. коэффициент отражения на входе 1 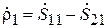 , или, с учётом (3.12), (3.13),
, или, с учётом (3.12), (3.13),
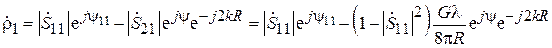 . (3.15)
. (3.15)
Следует отметить, что для реализации этого режима вовсе не обязательно иметь две идентичные антенны. Антенну 2, возбуждаемую в противофазе с антенной 1, можно заменить зеркальным изображением последней в идеально проводящем бесконечном экране, как показано на рис. 3.7.
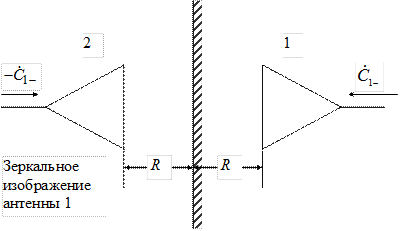
Рис. 3.7
Коэффициент усиления можно определить экспериментально, измеряя зависимость модуля коэффициента отражения 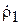 в линии 1 от расстояния R до экрана. Действительно, при изменении R в выражении (3.15) первое слагаемое остаётся неизменным, а второе меняется по фазе (изменениями его модуля при небольших изменениях R можно пренебречь). В результате модуль коэффициента отражения
в линии 1 от расстояния R до экрана. Действительно, при изменении R в выражении (3.15) первое слагаемое остаётся неизменным, а второе меняется по фазе (изменениями его модуля при небольших изменениях R можно пренебречь). В результате модуль коэффициента отражения 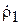 будет изменяться, и по зависимости его от R можно найти значения
будет изменяться, и по зависимости его от R можно найти значения 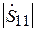 и
и 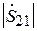 , подстановка которых в (3.14) позволит найти значение КУ G.
, подстановка которых в (3.14) позволит найти значение КУ G.
В процессе выполнения эксперимента возможны 2 случая.
Случай 1: 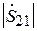 <
< 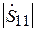 . В данном случае векторная диаграмма, соответствующая формуле (3.15), показана на рис. 3.8, а. При изменении расстояния R вектор
. В данном случае векторная диаграмма, соответствующая формуле (3.15), показана на рис. 3.8, а. При изменении расстояния R вектор 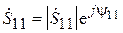 неподвижен, а вектор
неподвижен, а вектор 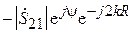 вращается вокруг конца вектора
вращается вокруг конца вектора 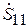 . Максимальное по модулю значение
. Максимальное по модулю значение 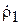 получится при совпадении фаз этих векторов. Пусть это имеет место при некотором расстоянии
получится при совпадении фаз этих векторов. Пусть это имеет место при некотором расстоянии 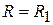 :
:
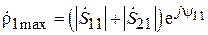 ,
, 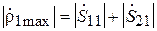 .
.
При изменении R на l/4 ( 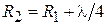 ) фаза вектора
) фаза вектора 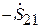 изменится на p и модуль коэффициента отражения
изменится на p и модуль коэффициента отражения 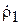 станет минимальным (рис. 3.8, б). Фаза его будет при этом той же, что и при
станет минимальным (рис. 3.8, б). Фаза его будет при этом той же, что и при 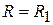 , т. е.
, т. е. 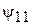 :
:
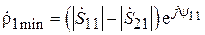 ,
, 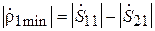 .
.
При 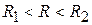 значения
значения 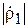 будут промежуточными между
будут промежуточными между 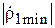 и
и 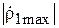 .
.
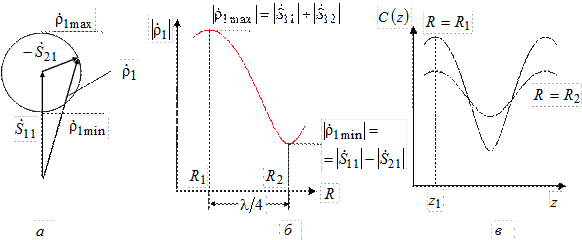
Рис. 3.8
Модули коэффициентов S-матрицы  и
и  будут, очевидно, определяться следующими выражениями:
будут, очевидно, определяться следующими выражениями:
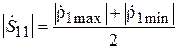 ,
, 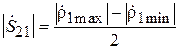 . (3.16)
. (3.16)
Обратим теперь внимание на следующий важный факт. При  во входной линии антенны создастся распределение поля C(z) с наименьшим значением КБВ, равным
во входной линии антенны создастся распределение поля C(z) с наименьшим значением КБВ, равным  (почему?). Пусть при этом максимум распределения поля расположен в некоторой точке с координатой
(почему?). Пусть при этом максимум распределения поля расположен в некоторой точке с координатой 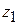 (рис. 3.8, в). При переходе к
(рис. 3.8, в). При переходе к 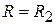 во входной линии будет распределение поля с максимально возможным КБВ, равным
во входной линии будет распределение поля с максимально возможным КБВ, равным 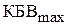 (почему?). При этом максимум поля в линии будет находиться в той же точке
(почему?). При этом максимум поля в линии будет находиться в той же точке 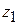 , что и при
, что и при 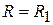 . Это связано с тем, что коэффициент отражения в линии в обоих случаях имеет одну и ту же фазу
. Это связано с тем, что коэффициент отражения в линии в обоих случаях имеет одну и ту же фазу 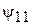 на входе 1.
на входе 1.
Случай 2: 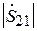 >
> 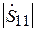 . Векторная диаграмма для
. Векторная диаграмма для 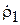 в этом случае показана на рис. 3.9, а. При
в этом случае показана на рис. 3.9, а. При 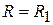 , как и в случае 1, при совпадении фаз векторов
, как и в случае 1, при совпадении фаз векторов 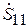 и
и 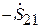 коэффициент отражения
коэффициент отражения 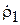 максимален по модулю:
максимален по модулю:
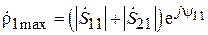 ,
, 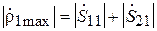 .
.
Фаза вектора 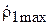 равна при этом
равна при этом 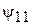 .
.
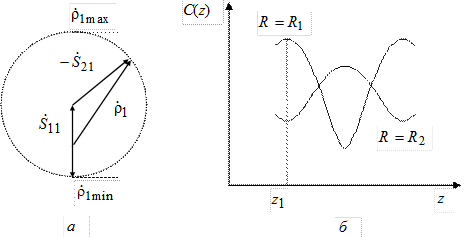
Рис. 3.9
При 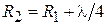 фаза вектора
фаза вектора  изменяется на p. При этом вектор
изменяется на p. При этом вектор 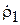 становится минимальным по модулю и равным
становится минимальным по модулю и равным
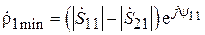 .
.
Это выражение совпадает с аналогичным для случая 1. Однако, поскольку 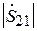 > >
> > 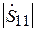 , разность в скобках перед экспонентой отрицательна. Модуль коэффициента отражения в этом случае
, разность в скобках перед экспонентой отрицательна. Модуль коэффициента отражения в этом случае 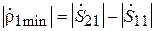 .
.
Полный комплексный коэффициент отражения
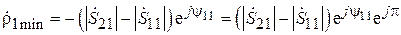 .
.
Таким образом, при переходе от 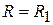 к
к 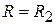 коэффициент отражения в линии изменяется по фазе на p, чего не наблюдалось в случае 1. Поэтому, если при
коэффициент отражения в линии изменяется по фазе на p, чего не наблюдалось в случае 1. Поэтому, если при 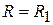 в точке z =
в точке z = 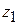 находился максимум распределения поля, то при
находился максимум распределения поля, то при 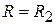 в той же точке будет минимум (рис. 3.9, б).
в той же точке будет минимум (рис. 3.9, б).
Модули элементов S-матрицы 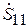 и
и 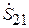 определяться следующим образом:
определяться следующим образом:
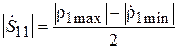 ,
, 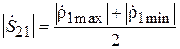 . (3.17)
. (3.17)
3.3. Лабораторный макет
Лабораторный макет (рис. 3.10) состоит из СВЧ-генератора 1, измерительной линии 2, индикаторного устройства 3, устройства перемещения антенны 4, исследуемой антенны 5 и экрана 6.
Изменение расстояния R производится перемещением антенны с помощью устройства 4. КБВ в линии, питающей исследуемую антенну, определя-
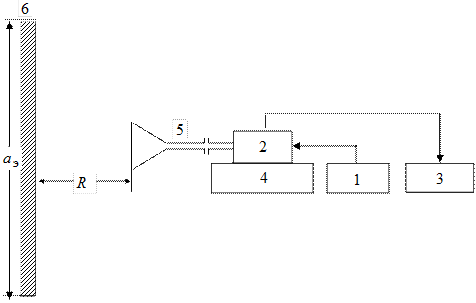
Рис. 3.10
ется с помощью измерительной линии 2 и индикатора 3. Экран 6 (металлический лист) закреплён неподвижно. Его размер 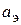 конечен, однако он достаточно хорошо имитирует бесконечный экран, если края листа видны из центра антенны под углом, не меньшим ширины главного лепестка ДН по нулевому уровню (т. е. поле излучения антенны в пределах главного лепестка полностью попадает на экран), что выполняется при условии
конечен, однако он достаточно хорошо имитирует бесконечный экран, если края листа видны из центра антенны под углом, не меньшим ширины главного лепестка ДН по нулевому уровню (т. е. поле излучения антенны в пределах главного лепестка полностью попадает на экран), что выполняется при условии
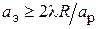 . (3.18)
. (3.18)
3.4. Проведение измерений
В данной лабораторной работе определяются параметры двух рупоров различных размеров. Размеры меньшего рупора следующие: 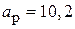 см,
см, 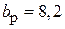 см,
см, 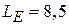 см,
см, 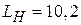 см. Размеры второго рупора:
см. Размеры второго рупора: 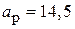 см,
см, 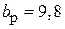 см,
см, 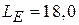 см,
см, 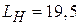 см.
см.
1. Включить генератор и индикаторный измеритель отношения напряжений. Частота генератора f заранее установлена. Рассчитать длину волны в свободном пространстве l = c / f, соответствующую данной частоте.
2. Подключить рупор к выходу измерительной линии и, изменяя расстояние от рупора до экрана R с шагом DR = l/10, снять зависимость модуля коэффициента отражения 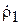 в линии от расстояния до экрана R (11 точек). Для этого при каждом R надо определить КСВ в измерительной линии и рассчитать
в линии от расстояния до экрана R (11 точек). Для этого при каждом R надо определить КСВ в измерительной линии и рассчитать 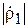 по формуле
по формуле 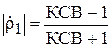 . Построить график зависимости
. Построить график зависимости 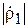 от R. С помощью построенного графика найти максимальное
от R. С помощью построенного графика найти максимальное 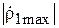 и минимальное
и минимальное 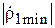 значения модуля коэффициента отражения
значения модуля коэффициента отражения 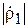 и определить расстояния
и определить расстояния 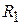 и
и 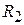 , при которых наблюдаются эти значения.
, при которых наблюдаются эти значения.
Измерение КСВ производится следующим образом. Зонд измерительной линии 2 (рис. 3.10) устанавливается в точку максимума поля. Стрелка индикаторного устройства с помощью регулировки усиления устанавливается на 1. Затем зонд измерительной линии перемещается в точку минимума поля и по нижней шкале индикатора считывается значение КСВ.
3. Установить расстояние до экрана 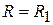 и поместить зонд измерительной линии в один из максимумов поля линии (z =
и поместить зонд измерительной линии в один из максимумов поля линии (z = 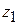 ).
).
4. Установить расстояние до экрана 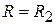 и выяснить, сохранился ли в точке
и выяснить, сохранился ли в точке  максимум поля (случай 1) или там сформировался минимум поля (случай 2).
максимум поля (случай 1) или там сформировался минимум поля (случай 2).
5. Выполнить задания пп. 2–4, заменив рупор 1 рупором 2.
3.5. Обработка результатов измерений
1. Рассчитать модули элементов матрицы рассеяния 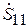 и
и 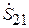 для обоих рупоров по формулам (3.16) и (3.17).
для обоих рупоров по формулам (3.16) и (3.17).
2. Рассчитать коэффициенты усиления рупоров G по формуле (3.14). Определить значение G1 в децибелах.
Примечание: при необходимости, при расчете коэффициентов усиления, следует в графиках рис. 3.3, 3.4 экстраполировать значение параметра.
3. Рассчитать теоретические значения коэффициентов усиления для обоих рупоров по формуле (3.8). КПД при этом принять равным единице.
4. Проверить непосредственным расчётом, что размер используемого экрана удовлетворяет условию (3.19).
3.6. Контрольные вопросы
1. Поясните механизм возникновения расфазировки поля в апертуре рупорной антенны.
2. Объясните характер влияния параметра 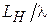 на диаграмму направленности Н-плоскостного рупора при
на диаграмму направленности Н-плоскостного рупора при 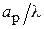 = const.
= const.
3. Поясните ход графиков зависимости приведённого КНД Н-плоскостного рупора 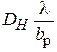 от
от 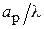 при
при 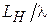 = const (по рис. 3.3).
= const (по рис. 3.3).
4. На графиках зависимости приведённого КНД Е-плоскостного рупора 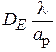 от
от 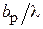 при
при 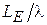 = const (см. рис. 3.4) виден осциллирующий характер этих зависимостей при
= const (см. рис. 3.4) виден осциллирующий характер этих зависимостей при 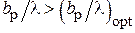 . Чем вызваны эти осцилляции?
. Чем вызваны эти осцилляции?
5. Почему максимальное-допустимое значение фазовой ошибки в Е-плоскостном рупоре меньше, чем в Н-плоскостном?
6. Поясните на качественном уровне, как в системе, изображённой на рис. 3.7, находится связь между 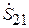 и параметрами антенн.
и параметрами антенн.
7. Покажите, что в схеме на рис. 3.6, поставленной в режим противофазного возбуждения, коэффициент отражения на входе 1 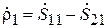 .
.
8. Сравните с точки зрения преимуществ и недостатков практической реализации метод зеркальных изображений и метод противофазного возбуждения двух идентичных антенн.
9. Прокомментируйте для случая 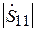 >
> 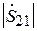 эволюцию коэффициента отражения
эволюцию коэффициента отражения 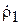 при изменении расстояния R.
при изменении расстояния R.
10. Прокомментируйте для случая 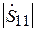 <
< 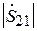 эволюцию коэффициента отражения
эволюцию коэффициента отражения 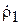 при изменении расстояния R.
при изменении расстояния R.
11. Поясните, как можно определить, какая из величин больше – 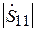 или
или 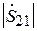 .
.
3.7. Содержание отчёта
Отчёт должен содержать:
1. Цель работы и структурную схему установки.
2. Расчет длины волны, на которой проводились измерения.
3. Результаты измерений зависимости КСВ от расстояния до экрана для разных антенн с указанием того, под какой случай 1) или 2) подпадает данная антенна.
4. Результаты расчётов (КУ рупоров следует представить в относительных единицах и в децибеллах).
5. Выводы по работе.
4. ИССЛЕДОВАНИЕ ЗЕРКАЛЬНОЙ АНТЕННЫ
4.1. Введение. Принцип действия зеркальной антенны
Зеркальные антенны (ЗА) – это основной тип антенн, применяемый в радиосистемах широкого назначения в тех случаях, когда требуется обеспечить простыми средствами высокую направленность (радиолокация, спутниковая связь) при минимальных тепловых потерях [7]. Нередко ЗА используются в установках с относительно медленным механическим сканированием. Идея построения остронаправленной ЗА состоит в следующем. Имеется слабонаправленный облучатель, т. е. небольшая антенна с широкой диаграммой направленности, которая облучает металлическое зеркало диаметром 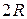 . Профиль зеркала подбирают таким образом, чтобы в его апертуре (раскрыве) сформировалось синфазное поле. При большом отношении
. Профиль зеркала подбирают таким образом, чтобы в его апертуре (раскрыве) сформировалось синфазное поле. При большом отношении 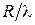 излучение апертуры зеркала будет остронаправленным с максимумом, ориентированным вдоль оптической оси системы (рис. 4.1). Для обеспечения синфазности поля в апертуре профиль зеркала должен быть параболическим, а облучатель
излучение апертуры зеркала будет остронаправленным с максимумом, ориентированным вдоль оптической оси системы (рис. 4.1). Для обеспечения синфазности поля в апертуре профиль зеркала должен быть параболическим, а облучатель
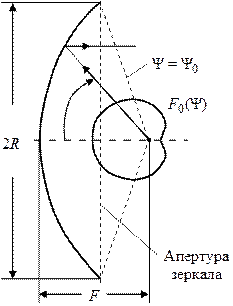
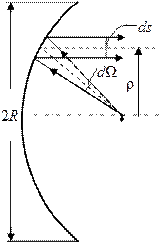
Рис. 4.1 Рис. 4.2
следует поместить в фокусе параболоида. В этом случае все радиолучи, расходящиеся из фокуса 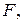 после отражения от зеркала пойдут параллельно фокальной оси – конический пучок лучей от облучателя преобразуется зеркалом в параллельный пучок. Поскольку поверхности равных фаз перпендикулярны семейству лучей, все они в отраженном пучке перпендикулярны фокальной оси. Следовательно, и апертура зеркала будет поверхностью равных фаз, т. е. во всех точках апертуры образуется синфазное поле. Геометрия параболического зеркала полностью определяется двумя параметрами – либо парой
после отражения от зеркала пойдут параллельно фокальной оси – конический пучок лучей от облучателя преобразуется зеркалом в параллельный пучок. Поскольку поверхности равных фаз перпендикулярны семейству лучей, все они в отраженном пучке перпендикулярны фокальной оси. Следовательно, и апертура зеркала будет поверхностью равных фаз, т. е. во всех точках апертуры образуется синфазное поле. Геометрия параболического зеркала полностью определяется двумя параметрами – либо парой 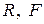 (фокусное расстояние), либо
(фокусное расстояние), либо 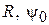 (угол облучения края зеркала).
(угол облучения края зеркала).
Значения R, F и 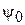 связаны друг с другом соотношением
связаны друг с другом соотношением 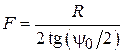 . Зеркала, имеющие угол облучения
. Зеркала, имеющие угол облучения 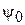 < 90о, называются длиннофокусными
< 90о, называются длиннофокусными 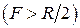 , а при
, а при 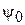 > 90о – короткофокусными.
> 90о – короткофокусными.
4.2. Теоретические сведения
Поле излучения плоской площадки. Пусть имеется плоская площадка 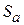 любой формы (рис. 4.3), в каждой точке которой заданы векторы электрического и магнитного полей:
любой формы (рис. 4.3), в каждой точке которой заданы векторы электрического и магнитного полей:
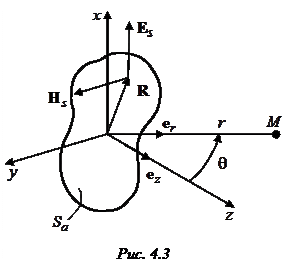
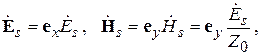
где 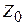 – волновое сопротивление среды, а
– волновое сопротивление среды, а 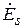 , вообще говоря, является функцией точки
, вообще говоря, является функцией точки 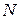 на поверхности площадки (
на поверхности площадки ( 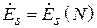 ). В теории излучения показано, что такая площадка создает в пространстве электромагнитное поле. В дальней зоне это поле (поле излучения) представляется в виде
). В теории излучения показано, что такая площадка создает в пространстве электромагнитное поле. В дальней зоне это поле (поле излучения) представляется в виде
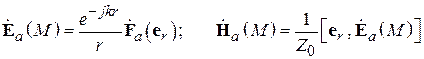 , (4.1)
, (4.1)
где 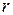 – расстояние от центра площадки
– расстояние от центра площадки 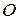 до точки наблюдения
до точки наблюдения 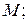
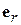 – орт, направленный из точки
– орт, направленный из точки 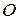 на точку
на точку 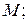
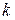 – волновое число.
– волновое число.
Точка 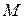 находится в дальней зоне, если удовлетворяются 3 неравенства:
находится в дальней зоне, если удовлетворяются 3 неравенства: 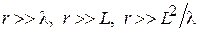 , где
, где 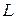 – наибольший линейный размер системы (излучающей площадки). Как видно из (4.1), поле в дальней зоне представляется в виде произведения двух функций – скалярной
– наибольший линейный размер системы (излучающей площадки). Как видно из (4.1), поле в дальней зоне представляется в виде произведения двух функций – скалярной 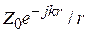 , зависящей только от расстояния
, зависящей только от расстояния 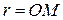 , и векторной
, и векторной 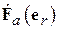 , зависящей от направления из
, зависящей от направления из 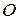 на точку наблюдения
на точку наблюдения 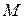 . Эта функция называется характеристикой
. Эта функция называется характеристикой 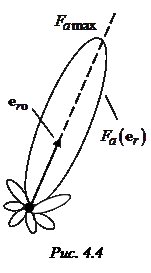 направленности излучающей площадки. Как и всякий вектор, ее можно представить в виде
направленности излучающей площадки. Как и всякий вектор, ее можно представить в виде 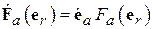 , где орт
, где орт 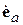 указывает пространственную ориентацию (поляризацию) вектора
указывает пространственную ориентацию (поляризацию) вектора 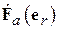 . Согласно (4.1), она совпадает с поляризацией вектора
. Согласно (4.1), она совпадает с поляризацией вектора 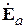 . Скалярная характеристика направленности
. Скалярная характеристика направленности 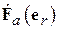 , которая несет информацию об амплитудном распределении поля излучения в зависимости от
, которая несет информацию об амплитудном распределении поля излучения в зависимости от 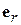 , может быть записана в виде произведения
, может быть записана в виде произведения 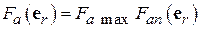 , где
, где 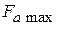 – значение характеристики направленности в направлении максимального излучения (орт
– значение характеристики направленности в направлении максимального излучения (орт 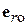 на рис. 4.4). Функция
на рис. 4.4). Функция 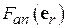 называется нормированной характеристикой направленности. Очевидно,
называется нормированной характеристикой направленности. Очевидно, 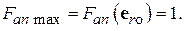
Характеристику направленности площадки можно рассчитать, если известно распределение поля 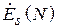 по ее поверхности
по ее поверхности 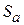 . В случае синфазного распределения поля (
. В случае синфазного распределения поля ( 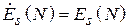 ) соответствующая формула выглядит так:
) соответствующая формула выглядит так:
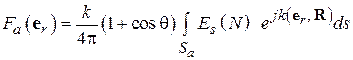 , (4.2)
, (4.2)
где вектор 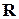 и угол
и угол 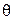 показаны на рис. 4.1. В данном случае направление максимального излучения нормально к
показаны на рис. 4.1. В данном случае направление максимального излучения нормально к  , т. е.
, т. е. 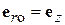 ,
,  = 0, а из (4.2) следует, что
= 0, а из (4.2) следует, что
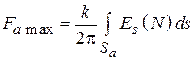 .
.
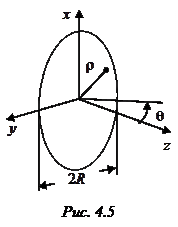 Круглая площадка с центрально-симметричным распределением поля. Допустим, что площадка имеет форму круга (рис. 4.5), а распределение поля
Круглая площадка с центрально-симметричным распределением поля. Допустим, что площадка имеет форму круга (рис. 4.5), а распределение поля 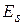 центрально-симметричное, т. е.
центрально-симметричное, т. е. 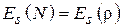 . В таком случае и характеристика направленности осесимметрична, т. е. является функцией одного угла
. В таком случае и характеристика направленности осесимметрична, т. е. является функцией одного угла 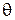 . После соответствующих преобразований интеграла (4.2) выражение для характеристики направленности такого раскрыва можно привести к следующему виду:
. После соответствующих преобразований интеграла (4.2) выражение для характеристики направленности такого раскрыва можно привести к следующему виду:
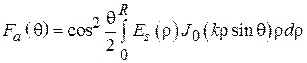 , (4.3)
, (4.3)
где 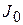 – функция Бесселя нулевого порядка.
– функция Бесселя нулевого порядка.
 Если распределение поля однородно, т. е.
Если распределение поля однородно, т. е. 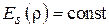 , то, используя (4.2) и (4.3), получим нормированную характеристику направленности в виде
, то, используя (4.2) и (4.3), получим нормированную характеристику направленности в виде
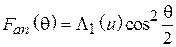 , (4.4)
, (4.4)
где 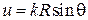 ,
, 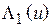 – лямбда-функция 1-го порядка [6]. При малых значениях угла
– лямбда-функция 1-го порядка [6]. При малых значениях угла 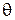 и больших значениях параметра kR можно считать, что
и больших значениях параметра kR можно считать, что 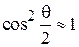 и зависимость
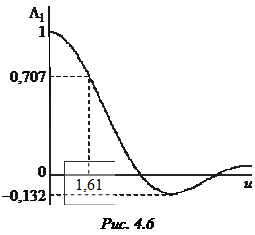
и зависимость 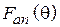 при малых углах определяется в основном первым множителем в (4.4). Вид функции
при малых углах определяется в основном первым множителем в (4.4). Вид функции 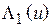 показан на рис. 4.6. Как видно, это осциллирующая функция, имеющая главный и ряд боковых лепестков. Ширина главного лепестка по уровню 0,707
показан на рис. 4.6. Как видно, это осциллирующая функция, имеющая главный и ряд боковых лепестков. Ширина главного лепестка по уровню 0,707
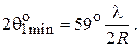 (4.5)
(4.5)
Формула (4.5) выражает фундаментальный факт: ширина главного лепестка определяется отношением радиуса площадки к длине волны. Чем больше отношение 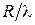 , тем уже лепесток, тем более остронаправленным является излучение. Заметим, что ширина диаграммы (4.5), полученная для однородного распределения поля, является минимально возможной при данном отношении
, тем уже лепесток, тем более остронаправленным является излучение. Заметим, что ширина диаграммы (4.5), полученная для однородного распределения поля, является минимально возможной при данном отношении 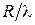 ; именно поэтому в (4.5) фигурирует индекс
; именно поэтому в (4.5) фигурирует индекс 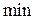 . В то же время при однородном распределении поля получается максимальный уровень первого бокового лепестка (0,132 или –17,6 дБ).
. В то же время при однородном распределении поля получается максимальный уровень первого бокового лепестка (0,132 или –17,6 дБ).
Если распределение поля по апертуре неоднородно ( 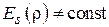 ), то для расчета характеристики направленности его удобно аппроксимировать полиномом вида
), то для расчета характеристики направленности его удобно аппроксимировать полиномом вида
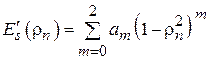 , (4.6)
, (4.6)
где 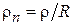 – нормированный радиус.
– нормированный радиус.
Приравнивая значения этого полинома и реального распределения 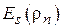 в точках
в точках 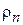 = 0; 0,5; 1,0 , для коэффициентов
= 0; 0,5; 1,0 , для коэффициентов 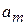 получим систему уравнений
получим систему уравнений 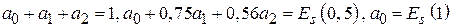 , решение которой дает следующие выражения для коэффициентов:
, решение которой дает следующие выражения для коэффициентов:
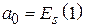 ,
, 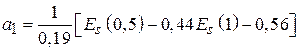 ,
, 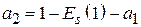 . (4.7)
. (4.7)
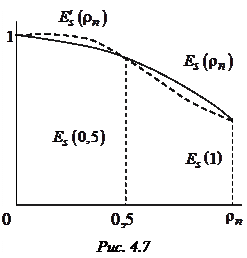 При практических расчетах после нахождения коэффициентов по (4.7) целесообразно рассчитать значения полинома и построить соответствующий график
При практических расчетах после нахождения коэффициентов по (4.7) целесообразно рассчитать значения полинома и построить соответствующий график 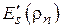 совместно с графиком истинного распределения
совместно с графиком истинного распределения 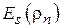 . Это даст возможность судить о качестве аппроксимации (рис. 4.7).
. Это даст возможность судить о качестве аппроксимации (рис. 4.7).
Примечание: Для повышения точности аппроксимации поля в ракрыве ЗА целесообразно записать систему уравнений более высокого порядка чем три (порядок равен выбранному числу узлов аппроксимации), затем решить ее численно и найти поле в раскрыве по формуле (4.6) с соответствующим числом членов суммы.
Подставляя аппроксимирующий полином (4.6) в формулу (4.3), получим нормированную характеристику направленности
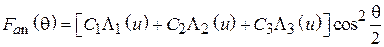 , (4.8)
, (4.8)
где коэффициенты 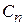 равны:
равны:
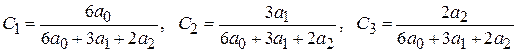 .
.
В (4.8) входят лямбда-функции 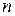 -го порядка
-го порядка 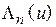 . Значения этих функций можно вычислить по формуле
. Значения этих функций можно вычислить по формуле 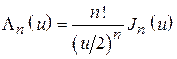 , где
, где 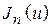 – функция Бесселя n-го порядка [6] .
– функция Бесселя n-го порядка [6] .
По рассчитанной характеристике направленности 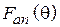 можно найти ширину ее главного лепестка
можно найти ширину ее главного лепестка 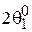 , которая окажется больше минимально возможной, найденной по формуле (4.5). Отношение
, которая окажется больше минимально возможной, найденной по формуле (4.5). Отношение 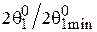 называется коэффициентом расширения луча (КРЛ). Эта величина показывает, во сколько раз ширина основного лепестка (луча) при данном распределении
называется коэффициентом расширения луча (КРЛ). Эта величина показывает, во сколько раз ширина основного лепестка (луча) при данном распределении 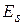 больше, чем при однородном распределении, но при том же значении
больше, чем при однородном распределении, но при том же значении 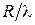 . Обычно КРЛ равен 1,1…1,3.
. Обычно КРЛ равен 1,1…1,3.
По рассчитанной характеристике 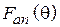 можно также найти уровень первого бокового лепестка (УБЛ). При распределении поля, спадающем от центра к краю апертуры, УБЛ оказывается меньше, нежели при однородном распределении (0,132). При этом, чем быстрее спадает поле, тем меньше УБЛ.
можно также найти уровень первого бокового лепестка (УБЛ). При распределении поля, спадающем от центра к краю апертуры, УБЛ оказывается меньше, нежели при однородном распределении (0,132). При этом, чем быстрее спадает поле, тем меньше УБЛ.
Коэффициент направленного действия и апертурный КИП площадки. Важнейшим параметром, характеризующим направленность любой антенны, является коэффициент направленного действия (КНД). По одному из нескольких эквивалентных определений КНД есть отношение плотности потока мощности на единицу телесного угла в направлении максимального излучения к средней по полному телесному углу  плотности потока мощности той же антенны.
плотности потока мощности той же антенны.
Свяжем это определение с характеристикой направленности. Известно, что величина 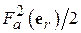 есть плотность потока мощности на единицу телесного угла в направлении орта
есть плотность потока мощности на единицу телесного угла в направлении орта 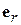 . Следовательно, в направлении максимального излучения она равна
. Следовательно, в направлении максимального излучения она равна 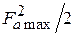 . Чтобы получить среднюю по телесному углу
. Чтобы получить среднюю по телесному углу 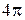 плотность потока мощности, нужно полную мощность
плотность потока мощности, нужно полную мощность 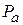 , излучаемую площадкой, разделить на
, излучаемую площадкой, разделить на 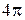 . Тогда, в соответствии с определением, КНД площадки
. Тогда, в соответствии с определением, КНД площадки
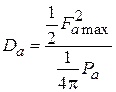 . (4.9)
. (4.9)
Величина, стоящая в числителе (4.9):
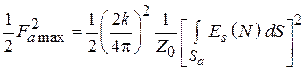 .
.
Значение мощности 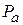 , входящее в знаменатель (4.9), можно найти через
, входящее в знаменатель (4.9), можно найти через 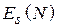 как поток вектора Пойнтинга через площадку
как поток вектора Пойнтинга через площадку 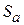 :
:
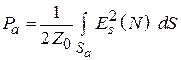 .
.
Тогда выражение (4.9) для КНД приводится к виду
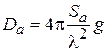 , (4.10)
, (4.10)
где
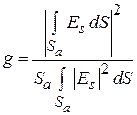 . (4.11)
. (4.11)
Как видно из (4.10), основным фактором, определяющим КНД синфазной апертуры, является отношение ее геометрической площади  к квадрату длины волны. С ростом этого отношения растет и КНД, что вполне согласуется с полученным ранее выводом о возрастании направленности излучения с ростом
к квадрату длины волны. С ростом этого отношения растет и КНД, что вполне согласуется с полученным ранее выводом о возрастании направленности излучения с ростом 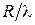 .
.
Коэффициент 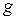 , входящий множителем в (4.10), учитывает влияние на КНД формы распределения поля
, входящий множителем в (4.10), учитывает влияние на КНД формы распределения поля 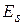 по площадке. Он называется апертурным коэффициентом использования площади (апертурный КИП). Из формулы (4.11) видно, что максимально возможное значение
по площадке. Он называется апертурным коэффициентом использования площади (апертурный КИП). Из формулы (4.11) видно, что максимально возможное значение 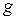 , равное 1, получается при равномерном распределении. При неравномерном распределении
, равное 1, получается при равномерном распределении. При неравномерном распределении 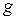 < 1. Обычно
< 1. Обычно 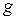 = 0,6...0,9. Поскольку апертурный КИП зависит только от распределения поля
= 0,6...0,9. Поскольку апертурный КИП зависит только от распределения поля 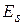 , его можно вычислить, зная коэффициенты аппроксимирующего полинома (4.6):
, его можно вычислить, зная коэффициенты аппроксимирующего полинома (4.6):
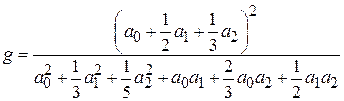 . (4.12)
. (4.12)
Распределение поля в апертуре параболического зеркала. Если диаграмма направленности облучателя 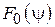 осесимметрична, т. е. зависит только от угла
осесимметрична, т. е. зависит только от угла 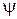 , то поле
, то поле 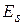 в апертуре будет центрально-симметричным:
в апертуре будет центрально-симметричным: 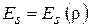 . Функция
. Функция 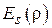 зависит от диаграммы облучателя
зависит от диаграммы облучателя 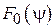 . Связь между этими двумя функциями можно установить с помощью условия энергетического баланса (рис. 4.2) в лучевых трубках до и после отражения от зеркала. Очевидно, в конической трубке с телесным углом
. Связь между этими двумя функциями можно установить с помощью условия энергетического баланса (рис. 4.2) в лучевых трубках до и после отражения от зеркала. Очевидно, в конической трубке с телесным углом 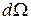 заключена та же мощность, что и в цилиндрической трубке с площадью
заключена та же мощность, что и в цилиндрической трубке с площадью 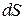 (см. рис. 4.2). Расчет показывает, что распределение поля
(см. рис. 4.2). Расчет показывает, что распределение поля 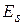 в функции нормированного радиуса
в функции нормированного радиуса 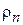 выражается через ДН облучателя следующим образом:
выражается через ДН облучателя следующим образом:
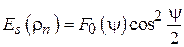 . (4.13)
. (4.13)
Постоянный множитель в (4.13) опущен, а нормированный радиус  и угол
и угол  связаны при этом жестким соотношением
связаны при этом жестким соотношением
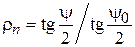 . (4.14)
. (4.14)
Расчет 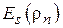 по известной ДН
по известной ДН 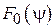 выполняется так. Задают последовательностью углов
выполняется так. Задают последовательностью углов 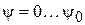 . Для каждого из них, зная
. Для каждого из них, зная  , находят по (4.14) значения
, находят по (4.14) значения 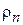 , а по (4.13) – соответствующие значения
, а по (4.13) – соответствующие значения 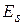 . По найденной функции
. По найденной функции 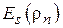 можно рассчитать нормированную характеристику направленности апертуры зеркала. Для этого нужно найти коэффициенты аппроксимирующего полинома и проверить качество аппроксимации. Далее рассчитываются коэффициенты
можно рассчитать нормированную характеристику направленности апертуры зеркала. Для этого нужно найти коэффициенты аппроксимирующего полинома и проверить качество аппроксимации. Далее рассчитываются коэффициенты 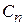 и нормированная ДН по формуле (4.8). Располагая этой ДН, можно найти ширину главного лепестка
и нормированная ДН по формуле (4.8). Располагая этой ДН, можно найти ширину главного лепестка  и КРЛ. Наконец, находятся апертурный КИП
и КРЛ. Наконец, находятся апертурный КИП  и КНД.
и КНД.
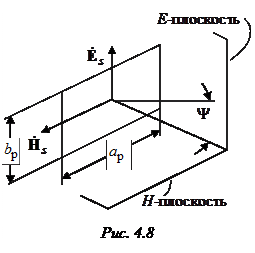 Облучатели зеркальных антенн. Одним из наиболее распространенных облучателей зеркальных антенн являются рупора с прямоугольным раскрывом, возбуждаемые прямоугольным волноводом (рис. 4.8). При их использовании возникает вопрос об осевой симметрии их диаграммы направленности, которая необходима для создания в апертуре зеркала осесимметричного распределения поля. Повлиять на ДН рупора можно только одним способом – выбором размеров апертуры
Облучатели зеркальных антенн. Одним из наиболее распространенных облучателей зеркальных антенн являются рупора с прямоугольным раскрывом, возбуждаемые прямоугольным волноводом (рис. 4.8). При их использовании возникает вопрос об осевой симметрии их диаграммы направленности, которая необходима для создания в апертуре зеркала осесимметричного распределения поля. Повлиять на ДН рупора можно только одним способом – выбором размеров апертуры 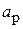 и
и 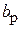 . Однако можно убедиться, что ни одна из комбинаций этих размеров не приводит к полностью осесимметричной ДН. Это видно хотя бы из того, что в плоскостях
. Однако можно убедиться, что ни одна из комбинаций этих размеров не приводит к полностью осесимметричной ДН. Это видно хотя бы из того, что в плоскостях 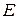 и
и 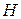 ДН рупора описываются разными функциями угла
ДН рупора описываются разными функциями угла 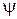 . В Е-плоскости это выражение имеет вид
. В Е-плоскости это выражение имеет вид
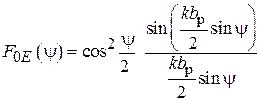 , (4.15)
, (4.15)
а в H-плоскости, соответственно,
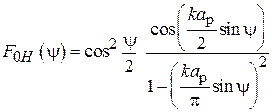 . (4.16)
. (4.16)
Поэтому возможно создание лишь приближенно осесимметричной ДН. Потребуем, чтобы значения ДН в обеих плоскостях совпали при  . Тогда процедура расчета размеров рупора может быть следующей. Известны угол
. Тогда процедура расчета размеров рупора может быть следующей. Известны угол  и уровень облучения края зеркала
и уровень облучения края зеркала 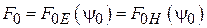 . Из (4.15) и (4.16) вытекают тогда следующие равенства:
. Из (4.15) и (4.16) вытекают тогда следующие равенства:
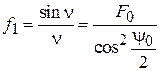 ,
, 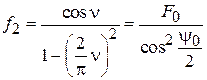 , (4.17)
, (4.17)
где 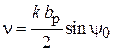 для функции f1 и
для функции f1 и 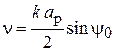 для функции f2. Разрешить равенства (4.17) относительно n можно, имея графики функций, стоящих в равенствах слева. Эти графики приведены на рис. 4.9. Зная n, а также
для функции f2. Разрешить равенства (4.17) относительно n можно, имея графики функций, стоящих в равенствах слева. Эти графики приведены на рис. 4.9. Зная n, а также  и
и  , легко найти
, легко найти  и
и  .
.
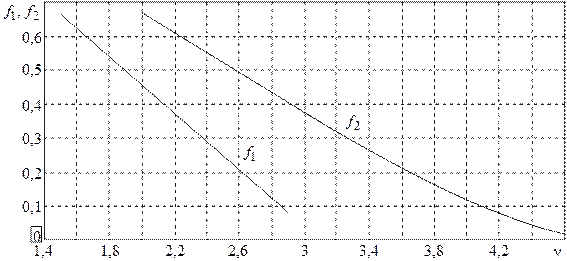
Рис. 4.9
Если размеры рупора выбраны из условия  , то диаграмму направленности
, то диаграмму направленности 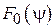 можно далее считать приближенно осесимметричной, а для ее аналитического представления использовать одну из формул (4.15) или (4.16). В дальнейшем остановимся на (4.15).
можно далее считать приближенно осесимметричной, а для ее аналитического представления использовать одну из формул (4.15) или (4.16). В дальнейшем остановимся на (4.15).
Переливание мощности через край зеркала. Эффективность облучателя. В зеркальных антеннах с облучателями традиционных типов (рупор, полуволновый вибратор с рефлектором и т. п.) не вся мощность облучателя 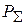 перехватывается зеркалом. Действительно, доля мощности
перехватывается зеркалом. Действительно, доля мощности 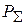 , соответствующая той части ДН облучателя, которая выходит за пределы угла 2y0 на рис. 4.6, переливается через край зеркала и не попадает в его апертуру. Это обстоятельство снижает КНД антенны в целом, который получается меньше КНД апертуры
, соответствующая той части ДН облучателя, которая выходит за пределы угла 2y0 на рис. 4.6, переливается через край зеркала и не попадает в его апертуру. Это обстоятельство снижает КНД антенны в целом, который получается меньше КНД апертуры 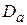 . По определению, КНД антенны представляется отношением типа (4.9)
. По определению, КНД антенны представляется отношением типа (4.9)
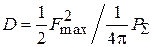 , (4.18)
, (4.18)
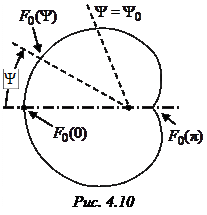 где
где 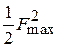 – плотность потока мощности антенны на единицу телесного угла в направлении ее максимального излучения. Строго говоря, в этом направлении складывается 2 поля – поле излучения апертуры и поле заднего излучения облучателя (рис. 4.10). Однако последнее обычно незначительно и им можно пренебречь. Следовательно, в (4.18) можно сделать замену
– плотность потока мощности антенны на единицу телесного угла в направлении ее максимального излучения. Строго говоря, в этом направлении складывается 2 поля – поле излучения апертуры и поле заднего излучения облучателя (рис. 4.10). Однако последнее обычно незначительно и им можно пренебречь. Следовательно, в (4.18) можно сделать замену 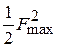 на
на 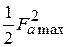 . Деля и умножая (4.18) на
. Деля и умножая (4.18) на 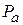 , получим
, получим
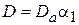 , (4.19)
, (4.19)
где 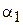 – отношение мощности, падающей на зеркало и проходящей затем апертуру (
– отношение мощности, падающей на зеркало и проходящей затем апертуру ( 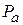 ), к полной мощности облучателя (
), к полной мощности облучателя ( 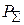 ). Это отношение и учитывает факт переливания мощности за край зеркала и называется эффективностью облучателя. Эффективность облучателя можно рассчитать по известной ДН облучателя и углу облучения края зеркала:
). Это отношение и учитывает факт переливания мощности за край зеркала и называется эффективностью облучателя. Эффективность облучателя можно рассчитать по известной ДН облучателя и углу облучения края зеркала:
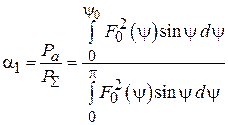 . (4.20)
. (4.20)
Подставляя (4.10) в (4.19), получим
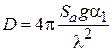 . (4.21)
. (4.21)
Максимизация КНД антенны. Обратим внимание на то, что при заданном угле облучения края зеркала 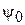 значения
значения 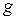 и
и 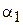 изменяются в зависимости от выбора ДН облучателя
изменяются в зависимости от выбора ДН облучателя 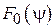 . При этом, если сужать эту ДН, то
. При этом, если сужать эту ДН, то 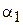 растет (см. (4.20)), а
растет (см. (4.20)), а 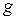 падает, ибо при этом увеличивается неравномерность распределения поля
падает, ибо при этом увеличивается неравномерность распределения поля 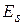 в апертуре. Следовательно, произведение
в апертуре. Следовательно, произведение 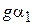 при определенной ширине диаграммы
при определенной ширине диаграммы 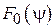 должно иметь максимум. При этом максимизируется и КНД (площадь апертуры и длина волны фиксированы). Выражая апертурный КИП через ДН облучателя, получим
должно иметь максимум. При этом максимизируется и КНД (площадь апертуры и длина волны фиксированы). Выражая апертурный КИП через ДН облучателя, получим
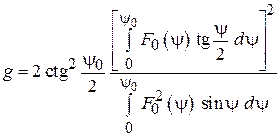 . (4.22)
. (4.22)
Составим произведение (4.20) и (4.22). Тогда
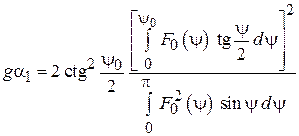 . (4.23)
. (4.23)
Если в качестве облучателя использовать рупор с приближенно осесимметричной ДН типа (4.15), то выражение (4.23) можно свести к следующему:
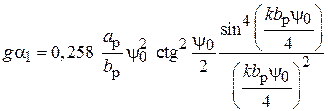 . (4.24)
. (4.24)
Считая, что угол 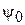 и отношение
и отношение 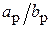 известны, видим, что
известны, видим, что 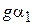 является функцией параметра
является функцией параметра 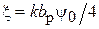 , входящего в последний множитель в (4.24). Можно показать, что этот множитель при x = 1,165 имеет максимальное значение, равное 0,525. Отсюда вытекает следующая рекомендация: для того чтобы зеркальная антенна с рупорным облучателем имела максимально возможный КНД, произведение
, входящего в последний множитель в (4.24). Можно показать, что этот множитель при x = 1,165 имеет максимальное значение, равное 0,525. Отсюда вытекает следующая рекомендация: для того чтобы зеркальная антенна с рупорным облучателем имела максимально возможный КНД, произведение 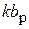 следует выбирать равным
следует выбирать равным
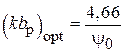 . (4.25)
. (4.25)
Таким образом, каждому углу  соответствует определенное оптимальное значение
соответствует определенное оптимальное значение  . Расчетная процедура, позволяющая найти оптимальный рупорный облучатель, иллюстрируется следующим примером.
. Расчетная процедура, позволяющая найти оптимальный рупорный облучатель, иллюстрируется следующим примером.
Задача. Угол облучения края зеркала  = 70º = 1,22 рад. Определить размеры рупора
= 70º = 1,22 рад. Определить размеры рупора 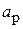 и
и 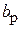 , для которых КНД антенны максимален (максимально произведение
, для которых КНД антенны максимален (максимально произведение 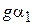 ) при
) при 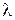 = 30 мм.
= 30 мм.
Решение. 1. Из (4.25) находим 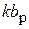 = 3,82. 2. Зная
= 3,82. 2. Зная 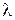 и
и 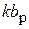 , находим
, находим 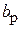 =
=
= 18,24 мм. 3. Размер 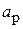 ищем, исходя из условия осевой симметрии ДН. Сначала находим уровень облучения края зеркала, используя (4.15) при
ищем, исходя из условия осевой симметрии ДН. Сначала находим уровень облучения края зеркала, используя (4.15) при 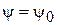 :
: 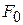 = 0,366. Далее, используя (4.16), получим
= 0,366. Далее, используя (4.16), получим 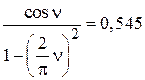 , где
, где 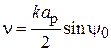 . Зная правую часть этого равенства, по графику на рис. 4.9 находим
. Зная правую часть этого равенства, по графику на рис. 4.9 находим 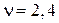 . Наконец, из выражения
. Наконец, из выражения 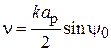 находим
находим 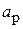 = 24,4 мм. Таким образом,
= 24,4 мм. Таким образом, 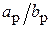 = 1,34. 4. Значение
= 1,34. 4. Значение 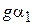 находим по (4.24), учитывая, что последний множитель равен 0,525:
находим по (4.24), учитывая, что последний множитель равен 0,525: 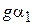 = 0,553.
= 0,553.
Как видно, произведение 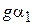 получилось заметно меньше единицы. Поэтому в стремлении повысить КНД зеркальных антенн разрабатывались облучатели, обладающие параметром
получилось заметно меньше единицы. Поэтому в стремлении повысить КНД зеркальных антенн разрабатывались облучатели, обладающие параметром 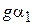 , близким к единице. Чтобы этого добиться, нужно сформировать такую ДН облучателя, при которой распределение поля в апертуре было бы однородным (тогда
, близким к единице. Чтобы этого добиться, нужно сформировать такую ДН облучателя, при которой распределение поля в апертуре было бы однородным (тогда  = 1) и отсутствовало бы переливание мощности за край зеркала (тогда
= 1) и отсутствовало бы переливание мощности за край зеркала (тогда  = 1). Этим требованиям удовлетворяет гипотетический облучатель с диаграммой вида
= 1). Этим требованиям удовлетворяет гипотетический облучатель с диаграммой вида
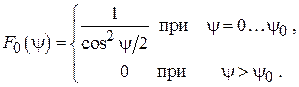 (4.26)
(4.26)
Точная реализация ДН (4.26) невозможна, однако существуют облучатели с ДН, близкими к (4.26).
Снижение КНД вследствие затенения апертуры. Облучатель, имеющий некоторую площадь раскрыва 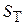 , частично затеняет апертуру зеркала. Это приводит к уменьшению КНД апертуры и антенны в целом и учитывается множителем
, частично затеняет апертуру зеркала. Это приводит к уменьшению КНД апертуры и антенны в целом и учитывается множителем 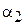 , который вводится в выражение для КНД и носит название прозрачности апертуры. Его приближенно можно рассчитать по формуле
, который вводится в выражение для КНД и носит название прозрачности апертуры. Его приближенно можно рассчитать по формуле 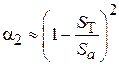 . Таким образом, окончательное выражение для КНД антенны с учетом (4.21) будет следующим:
. Таким образом, окончательное выражение для КНД антенны с учетом (4.21) будет следующим:
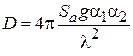 . (4.27)
. (4.27)
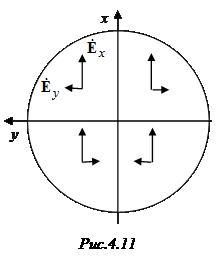 Кроссполяризация. При рассмотрении излучения апертуры предполагалось, что вектор
Кроссполяризация. При рассмотрении излучения апертуры предполагалось, что вектор  во всех ее точках поляризован вдоль орта
во всех ее точках поляризован вдоль орта  , как показано на рис. 4.11. Однако в реальных зеркальных антеннах процессы, происходящие при отражении поля излучателя от зеркала, таковы, что в апертуре появляется помимо основной (вертикальной) составляющей поля
, как показано на рис. 4.11. Однако в реальных зеркальных антеннах процессы, происходящие при отражении поля излучателя от зеркала, таковы, что в апертуре появляется помимо основной (вертикальной) составляющей поля  перпендикулярная ей горизонтальная составляющая. Эта так называемая кроссполяризационная составляющая имеет в разных квадрантах зеркала различную полярность (рис. 4.11). Уровень кроссполяризационной составляющей зависит от угла облучения края зеркала – чем меньше этот угол, тем ниже уровень кроссполяризации. Этот уровень также существенно зависит от типа облучателя. В частности, известно, что при облучателе типа диполя Герца уровень кроссполяризации достаточно высок. В то же время при облучателе в виде элемента Гюйгенса кроссполяризация практически отсутствует. Поскольку рупорные облучатели в определенном смысле близки к элементу Гюйгенса, их применение с этой точки зрения более предпочтительно. Обычно доля кроссполяризационного излучения по сравнению с излучением по основной составляющей составляет единицы процента по мощности.
перпендикулярная ей горизонтальная составляющая. Эта так называемая кроссполяризационная составляющая имеет в разных квадрантах зеркала различную полярность (рис. 4.11). Уровень кроссполяризационной составляющей зависит от угла облучения края зеркала – чем меньше этот угол, тем ниже уровень кроссполяризации. Этот уровень также существенно зависит от типа облучателя. В частности, известно, что при облучателе типа диполя Герца уровень кроссполяризации достаточно высок. В то же время при облучателе в виде элемента Гюйгенса кроссполяризация практически отсутствует. Поскольку рупорные облучатели в определенном смысле близки к элементу Гюйгенса, их применение с этой точки зрения более предпочтительно. Обычно доля кроссполяризационного излучения по сравнению с излучением по основной составляющей составляет единицы процента по мощности.
4.2. Экспериментальная установка
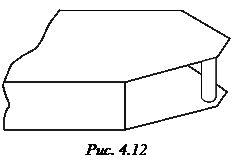 В экспериментальной установке используется зеркало с параметрами
В экспериментальной установке используется зеркало с параметрами 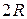 = 310 мм,
= 310 мм, 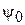 = 51,69º (
= 51,69º ( 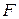 = 160 мм). Имеются два сменных облучателя: № 1 – рупорный с
= 160 мм). Имеются два сменных облучателя: № 1 – рупорный с 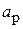 = 40,5 мм,
= 40,5 мм, 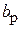 = 32 мм и № 2 – открытый конец волновода со срезанными углами и металлическим стержнем в центре раскрыва (рис. 4.12). Такой облучатель имеет существенно более широкую ДН, нежели открытый конец волновода в «чистом виде». Кроме того, его диаграмма имеет провал вдоль оси излучателя, что способствует созданию более равномерного распределения поля в апертуре зеркала.
= 32 мм и № 2 – открытый конец волновода со срезанными углами и металлическим стержнем в центре раскрыва (рис. 4.12). Такой облучатель имеет существенно более широкую ДН, нежели открытый конец волновода в «чистом виде». Кроме того, его диаграмма имеет провал вдоль оси излучателя, что способствует созданию более равномерного распределения поля в апертуре зеркала.
В установке имеется возможность снятия диаграмм направленности как облучателей, так и антенны в целом. При снятии ДН следует совмещать ось вращения поворотного устройства с раскрывом исследуемой антенны. В качестве приемной антенны используется рупор с установленной в тракте питания детекторной секцией. После детектирования сигнал поступает на измерительный усилитель. Установка работает в трехсантиметровом диапазоне волн.
4.3. Эксперимент
1. Включить генератор и измерительный усилитель. Генератор настроить на частоту, заданную преподавателем. Рассчитать соответствующую длину волны в свободном пространстве 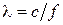 .
.
2. Измерить диаграмму направленности облучателя № 1 в горизонтальной плоскости, измерения следует проводить с шагом 10º. Повторить те же измерения с облучателем № 2
3. Измерить диаграмму направленности зеркальной антенны с облучателем № 1 и № 2 в области углов 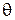 , соответствующих главному и первому боковому лепесткам. Шаг при этом должен быть значительно меньше, чем в предыдущем случае – порядка 1º.
, соответствующих главному и первому боковому лепесткам. Шаг при этом должен быть значительно меньше, чем в предыдущем случае – порядка 1º.
4.4. Обработка результатов эксперимента.
1. Снятые диаграммы направленности антенн нормировать к единице 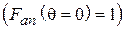 и построить их графики. Определить по ним ширину основного лепестка
и построить их графики. Определить по ним ширину основного лепестка  . Рассчитать минимальную ширину ДН (4.5) и определить КРЛ. Найти также значение УБЛ.
. Рассчитать минимальную ширину ДН (4.5) и определить КРЛ. Найти также значение УБЛ.
2. Нормировать к единице измеренные ДН облучателей (F0(0) = 1) и построить их графики.
3. По измеренной ДН 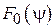 рассчитать распределение поля в апертуре
рассчитать распределение поля в апертуре 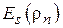 и построить его график.
и построить его график.
4. По полученному распределению 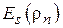 найти значения
найти значения 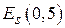 и полинома.
и полинома.
5. Рассчитать значения аппроксимирующего полинома 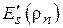 и построить их графики совместно с графиками
и построить их графики совместно с графиками 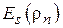 . Оценить качество аппроксимации.
. Оценить качество аппроксимации.
6. Рассчитать апертурный КИП 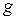 по формуле (4.12).
по формуле (4.12).
7. Рассчитать коэффициенты 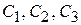 по формулам (4.8) и ДН зеркальной антенны. Построить соответствующие графики.
по формулам (4.8) и ДН зеркальной антенны. Построить соответствующие графики.
8. Определить по расчетным графикам ширину главного лепестка ДН 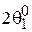 и КРЛ. Сравнить их с соответствующими экспериментальными значениями.
и КРЛ. Сравнить их с соответствующими экспериментальными значениями.
9. Рассчитать по формуле (4.24) параметр 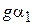 . Зная
. Зная 
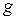 , найти эффективность облучателя
, найти эффективность облучателя 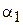 . По формуле (4.27) найти КНД этой антенны. Данный пункт относится к случаю антенны с рупорным облучателем.
. По формуле (4.27) найти КНД этой антенны. Данный пункт относится к случаю антенны с рупорным облучателем.
4.5. Контрольные вопросы
1. Какие предположения относительно полей 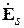 и
и 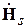 на излучающей поверхности
на излучающей поверхности 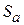 приняты в рамках данной работы?
приняты в рамках данной работы?
2. Каков физический смысл характеристики направленности излучающей системы 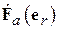 ? Прокомментируйте ее представления в виде
? Прокомментируйте ее представления в виде 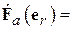
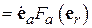 и
и 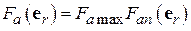 .
.
3. Какие факторы определяют форму скалярной характеристики направленности синфазной излучающей площадки?
4. Как зависит ширина главного лепестка характеристики направленности круглой площадки от ее радиуса и длины волны?
5. При каком распределении поля  по излучающей площадке ширина главного лепестка ДН минимальна? Что такое КРЛ?
по излучающей площадке ширина главного лепестка ДН минимальна? Что такое КРЛ?
6. Как зависит УБЛ от скорости убывания поля  от центра к краю излучающей круглой площадки?
от центра к краю излучающей круглой площадки?
7. Дайте определение КНД любой излучающей системы. Как зависит КНД синфазной площадки от ее геометрической площади, длины волны и формы распределения поля по площадке?
8. Как практически рассчитать апертурный КИП по известному распределению поля на круглой площадке 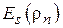 ?
?
9. Поясните принцип действия зеркальной антенны.
10. Как связано распределение поля по апертуре зеркала с ДН облучателя?
11. В какой последовательности нужно действовать, чтобы, зная геометрию зеркала ( 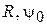 ) и ДН облучателя
) и ДН облучателя 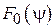 , найти ДН апертуры, КРЛ, апертурный КИП и КНД?
, найти ДН апертуры, КРЛ, апертурный КИП и КНД?
12. Как следует действовать, чтобы рассчитать электрические размеры рупорного облучателя 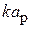 и
и 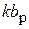 при известном угле облучения края зеркала
при известном угле облучения края зеркала 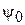 и заданном уровне его облучения, одинаковом в плоскостях
и заданном уровне его облучения, одинаковом в плоскостях 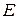 и
и 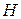 ?
?
13. Что такое эффективность облучателя 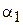 и от каких факторов она зависит? Как зависит КНД зеркальной антенны от площади апертуры, длины волны, апертурного КИП и эффективности облучателя?
и от каких факторов она зависит? Как зависит КНД зеркальной антенны от площади апертуры, длины волны, апертурного КИП и эффективности облучателя?
14. Как объяснить на качественном уровне тот факт, что при изменении ширины ДН облучателя произведение 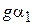 принимает максимальное значение?
принимает максимальное значение?
15. Как связаны между собой оптимальный электрический размер рупорного облучателя 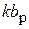 и угол облучения края зеркала
и угол облучения края зеркала 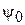 ? Как, зная
? Как, зная 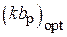 , найти затем соответствующий размер
, найти затем соответствующий размер 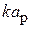 ?
?
16. Какой диаграммой направленности теоретически должен обладать облучатель, чтобы произведение 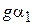 было равно 1?
было равно 1?
17. Какие причины вызывают затенение апертуры зеркала и как это сказывается на КНД антенны?
18. Что такое кроссполяризация и какие факторы влияют на уровень кроссполяризационного поля?
19. Как выяснить, на каком минимальном расстоянии должна находиться приемная антенна от исследуемой зеркальной антенны, чтобы снимаемая ДН совпадала с ее действительной ДН?
20. В каком случае уровень сигнала в приемной антенне будет выше: при снятии ДН облучателей или при снятии ДН зеркальной антенны в области главного и ближних боковых лепестков?
4.6. Содержание отчета
Отчет должен содержать:
· Структурную схему установки;
· Таблицы и графики экспериментальных ДН облучателей и ЗА с ними;
· Расчетные графики поля в раскрыве ЗА;
· Расчетные ДН антенн в виде графиков;
· Расчет ШГЛ, КНД, КРЛ, УБЛ;
· Выводы.
5. ВЛИЯНИЕ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ
НА ДИАГРАММЫ НАПРАВЛЕННОСТИ АНТЕНН
При расположении антенны над проводящей поверхностью ее ДН претерпевает существенные изменения по сравнению с характеристиками в свободном пространстве. В некоторых частотных диапазонах (СДВ, ДВ, СВ) земля и водная поверхность могут рассматриваться как поверхности с хорошей проводимостью, в связи с этим исследование влияния подстилающей поверхности на характеристики антенн и ее учет при разработке, размещении и выборе поляризации излучения антенн позволяет улучшить характеристики радиотехнических систем.
Учет эффектов влияния проводящей поверхности на ДН антенн в лабораторной работе проводится на основе метода зеркальных изображений. Он позволяет провести решение электродинамических задач при наличии границ раздела сред и найти электрические и магнитные поля, создаваемые антенной, расположенной вблизи проводящей поверхности. Суть метода заключается в том, что, путем введения фиктивного источника, задача поиска полей в присутствии проводящей поверхности сводится к более простой задаче в свободном пространстве. При этом величину поля, создаваемого фиктивным источником, и его расположение определяют из условия обеспечения граничных условий.
В данной лабораторной работе экспериментально и теоретически исследуются характеристики антенны в виде открытого конца волновода, расположенного над проводящей поверхностью, и определяется поведение ДН антенны при изменении высоты подъема антенны для различных поляризаций излучаемого поля.
5.1. Идея метода зеркальных изображений
 Рассмотрим следующую ситуацию. Имеется источник поля, расположенный над бесконечной идеально проводящей поверхностью S (рис. 5.1), которая делит пространство на два полупространства – 1 и 2. В полупространстве 2 поле отсутствует, так как оно экранировано от источника. Требуется найти поле в полупространстве 1, которое, очевидно, не совпадает с полем источника в отсутствие экрана. С формально-математической точки зрения влияние экрана сказывается в том, что на его поверхности должно выполняться граничное условие
Рассмотрим следующую ситуацию. Имеется источник поля, расположенный над бесконечной идеально проводящей поверхностью S (рис. 5.1), которая делит пространство на два полупространства – 1 и 2. В полупространстве 2 поле отсутствует, так как оно экранировано от источника. Требуется найти поле в полупространстве 1, которое, очевидно, не совпадает с полем источника в отсутствие экрана. С формально-математической точки зрения влияние экрана сказывается в том, что на его поверхности должно выполняться граничное условие
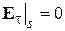 ,
, 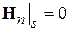 . (5.1)
. (5.1)
Метод зеркальных изображений позволяет рассчитать поле в полупространстве 1 путем замены экрана зеркальным изображением источника в нем. Искомое поле представляется тогда суммой полей истинного источника и его зеркального изображения. На месте удаленного экрана должно при этом обеспечиваться выполнение условия (5.1). Рассмотрим применение метода на примере вертикального и горизонтального диполя Герца с моментом 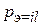 (
(  -ток, l-длина диполя) (рис. 5.2). На основе метода зеркальных изображений откажемся от проводящей границы раздела и запишем выражение для напряженности электрического поля, создаваемого в дальней зоне диполя Герца с моментом pэ в следующем виде:
-ток, l-длина диполя) (рис. 5.2). На основе метода зеркальных изображений откажемся от проводящей границы раздела и запишем выражение для напряженности электрического поля, создаваемого в дальней зоне диполя Герца с моментом pэ в следующем виде: 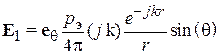 . На фиктивной границе двух сред орт
. На фиктивной границе двух сред орт 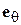 можно представить как сумму нормальной и касательной к поверхности, составляющей со своими амплитудными коэффициентами
можно представить как сумму нормальной и касательной к поверхности, составляющей со своими амплитудными коэффициентами 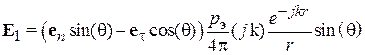 . Из приведенного выражения видно, что одиночной диполь имеет отличную от нуля касательную к поверхности составляющую электрического поля, что не удовлетворяет ГУ (5.1). В связи с этим необходимо осуществить выбор расположения и фазы дипольного момента изображения, при которых обеспечивается выполнение ГУ. Поле мнимого изображения должно скомпенсировать касательную составляющую электрического поля оригинала, следовательно, моменты оригинала и изображения должны быть синфазными. В этом случае поле, создаваемое изображением, запишется как
. Из приведенного выражения видно, что одиночной диполь имеет отличную от нуля касательную к поверхности составляющую электрического поля, что не удовлетворяет ГУ (5.1). В связи с этим необходимо осуществить выбор расположения и фазы дипольного момента изображения, при которых обеспечивается выполнение ГУ. Поле мнимого изображения должно скомпенсировать касательную составляющую электрического поля оригинала, следовательно, моменты оригинала и изображения должны быть синфазными. В этом случае поле, создаваемое изображением, запишется как 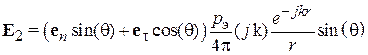 . В результате суммарное поле будет удовлетворять ГУ (5.1) и таким образом, поле в дальней зоне системы из двух источников окажется эквивалентным полю диполя над проводящей поверхностью.
. В результате суммарное поле будет удовлетворять ГУ (5.1) и таким образом, поле в дальней зоне системы из двух источников окажется эквивалентным полю диполя над проводящей поверхностью.
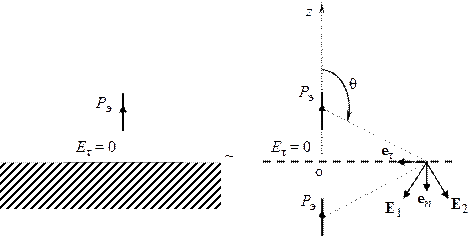
Рис. 5.2
Повторяя изложенные рассуждения для горизонтально расположенного диполя можно сделать вывод, что в этом случае моменты должны быть противофазными.
5.2. Применение метода зеркальных изображений к антеннам,
размещенным над проводящей плоскостью
Как известно, любую антенну можно представить совокупностью элементарных электрических и магнитных диполей Герца. Поэтому очевидна законность переноса метода зеркальных изображений и на этот случай. Суть метода полностью сохраняется: чтобы найти поле антенны в полупространстве 1, нужно отбросить экран, а его действие заменить действием зеркального изображения антенны. Необходимо лишь выяснить связь между характеристиками направленности реальной антенны и ее зеркального отображения. Для удобства анализа рассмотрим отдельно случай антенны с вертикально- и горизонтально-поляризованным полями излучения.
|
Вертикальная поляризация. Пусть центр О1 антенны 1 поднят над поверхностью на высоту h (рис. 5.3). Центр изображения (антенны 2) должен, очевидно, находиться в зеркально-симметричной точке О2. Суммарное напряженность электрического поля обеих антенн должно иметь нулевую касательную составляющую в любой точке А на поверхности S. Определим сна 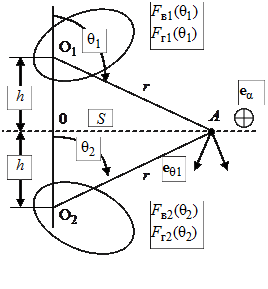 чала в этой точке поле антенны 1. Как известно, в поле излучения вектор электрического поля
чала в этой точке поле антенны 1. Как известно, в поле излучения вектор электрического поля  перпендикулярен направлению распространения, т. е. в данном случае - лучу О1А; в то же время этот вектор, по нашему предположению, поляризован в вертикальной плоскости. Следовательно, он должен быть ориентирован по орту
перпендикулярен направлению распространения, т. е. в данном случае - лучу О1А; в то же время этот вектор, по нашему предположению, поляризован в вертикальной плоскости. Следовательно, он должен быть ориентирован по орту  . Поле излучения пропорционально характеристике направленности по направлению луча О1А. Характеристика направленности антенны 1 записывается как функция угла
. Поле излучения пропорционально характеристике направленности по направлению луча О1А. Характеристика направленности антенны 1 записывается как функция угла  , отсчитываемого от вертикали. Следовательно, ее значение по направлению луча О1А есть
, отсчитываемого от вертикали. Следовательно, ее значение по направлению луча О1А есть 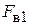 (
( 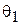 ). Наконец, выражение для поля
). Наконец, выражение для поля 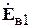 [В/м] должно содержать множитель, учитывающий запаздывание волны по фазе и убывание ее по амплитуде обратно пропорционально расстоянию от антенны. Этот множитель - функция Грина
[В/м] должно содержать множитель, учитывающий запаздывание волны по фазе и убывание ее по амплитуде обратно пропорционально расстоянию от антенны. Этот множитель - функция Грина 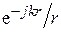 . Учитывая изложенное, получим
. Учитывая изложенное, получим
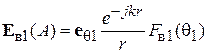 . (5.2)
. (5.2)
Аналогичным образом записывается поле зеркального изображения в точке А:
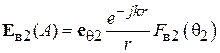 , (5.3)
, (5.3)
где 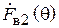 – характеристика направленности антенны 2. Угол
– характеристика направленности антенны 2. Угол  по-прежнему отсчитывается от вертикали, так что в данном случае он равен
по-прежнему отсчитывается от вертикали, так что в данном случае он равен 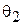 (см. рис. 5.3).
(см. рис. 5.3).
Чтобы поле 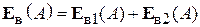 , полученное суммированием (5.2) и (5.3), имело нулевую касательную составляющую относительно S, значения
, полученное суммированием (5.2) и (5.3), имело нулевую касательную составляющую относительно S, значения 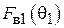 и
и 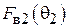 должны совпадать. Только в этом случае касательные составляющие обоих полей взаимно компенсируются. Заметим, что углы
должны совпадать. Только в этом случае касательные составляющие обоих полей взаимно компенсируются. Заметим, что углы 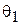 и
и 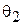 в данном рассмотрении жестко связаны:
в данном рассмотрении жестко связаны: 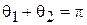 . Поэтому
. Поэтому 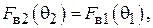
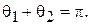 Это равенство означает, что характеристика направленности антенны 2 должна быть зеркальным отражением характеристики направленности антенны 1 (см. рис. 5.3), а антенны должны быть возбуждены синфазно.
Это равенство означает, что характеристика направленности антенны 2 должна быть зеркальным отражением характеристики направленности антенны 1 (см. рис. 5.3), а антенны должны быть возбуждены синфазно.
 Особо выделим случай, когда ДН антенны 1 симметрична относительно направления
Особо выделим случай, когда ДН антенны 1 симметрична относительно направления  (рис. 5.4). В таком случае ее зеркальное изображение будет совпадать с оригиналом. Следовательно,
(рис. 5.4). В таком случае ее зеркальное изображение будет совпадать с оригиналом. Следовательно,
 . (5.4)
. (5.4)
Горизонтальная поляризация. В данном случае выражение для поля антенны 1 в точке А  будет отличаться от выражения (5.3). Во-первых, вектор
будет отличаться от выражения (5.3). Во-первых, вектор  , который должен быть перпендикулярен О1А (см. рис. 5.3) и одновременно горизонтально поляризован, будет направлен по орту
, который должен быть перпендикулярен О1А (см. рис. 5.3) и одновременно горизонтально поляризован, будет направлен по орту  , перпендикулярному плоскости рисунка. Во-вторых, характеристика направленности имеет индекс «г», а не «в». Таким образом,
, перпендикулярному плоскости рисунка. Во-вторых, характеристика направленности имеет индекс «г», а не «в». Таким образом,
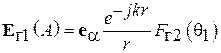 . (5.5)
. (5.5)
Поле антенны 2 также поляризовано по орту 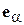 :
:
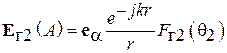 . (5.6)
. (5.6)
Сумма векторов (5.5) и (5.6) должна обратиться в нуль, поскольку орт  касателен к S. Следовательно, значения
касателен к S. Следовательно, значения  и
и 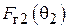 должны быть равны и противоположны по знаку:
должны быть равны и противоположны по знаку:
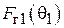 = -
= - 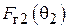 ,
, 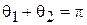 . (5.7)
. (5.7)
Таким образом, характеристики направленности антенн являются зеркальными изображениями друг друга, но, согласно (5.7) в отличие от вертикальной поляризации (см. (5.4)), антенны должны быть возбуждены в противофазе.
В особом случае, когда характеристики направленности симметричны относительно  , получим следующее соотношение между ними:
, получим следующее соотношение между ними:
 . (5.8)
. (5.8)
5.3. Обобщение на антенны с произвольно
поляризованным излучением
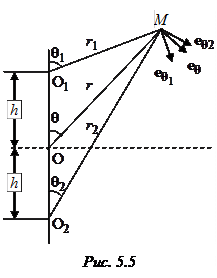 В общем случае поле излучения антенны имеет вертикальную и горизонтальную составляющие, причем каждая из них обладает своей характеристикой направленности. Полное поле каждой из антенн представляется как сумма вертикальной и горизонтальной составляющих. Запишем поле антенны 1 в произвольной точке М 1-го полупространства (рис. 5.5). Для этого сложим выражения (5.2) и (5.5), подставляя в них координаты точки М:
В общем случае поле излучения антенны имеет вертикальную и горизонтальную составляющие, причем каждая из них обладает своей характеристикой направленности. Полное поле каждой из антенн представляется как сумма вертикальной и горизонтальной составляющих. Запишем поле антенны 1 в произвольной точке М 1-го полупространства (рис. 5.5). Для этого сложим выражения (5.2) и (5.5), подставляя в них координаты точки М:
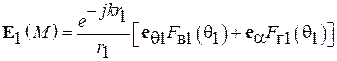 . (5.9)
. (5.9)
В той же точке М поле зеркального изображения равно
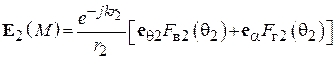 . (5.10)
. (5.10)
Если точка наблюдения находится в дальней зоне системы «антенна 1 - антенна 2», то выполняются неравенства  >>
>>  ,
,  >>
>> 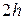 ,
, 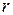 >>
>> 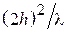 . В этом случае выражения (5.9) и (5.10) можно упростить. При выполнении указанных неравенств лучи О1М и О2М практически параллельны; поэтому
. В этом случае выражения (5.9) и (5.10) можно упростить. При выполнении указанных неравенств лучи О1М и О2М практически параллельны; поэтому 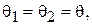
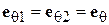 . Кроме того, в знаменателях (5.9) и (5.10) можно положить
. Кроме того, в знаменателях (5.9) и (5.10) можно положить 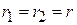 . Тогда
. Тогда
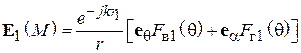 , (5.11)
, (5.11)
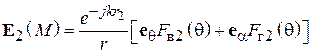 . (5.12)
. (5.12)
Наконец, примем, что характеристики направленности и по горизонтальной, и по вертикальной составляющим симметричны относительно 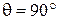 . Тогда действуют связи (5.4) и (5.8). Учитывая их, преобразуем (5.12):
. Тогда действуют связи (5.4) и (5.8). Учитывая их, преобразуем (5.12):
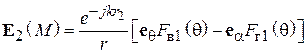
 . (5.13)
. (5.13)
Следует отметить, что поля антенн 1 и 2 из-за разницы знака при 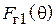 в (5.11) и (5.13) поляризованы неодинаково. Допустим, например, что
в (5.11) и (5.13) поляризованы неодинаково. Допустим, например, что 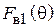 и
и 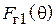 равны по модулю и сдвинуты по фазе на 90º, так что квадратную скобку в (5.11) можно записать в виде
равны по модулю и сдвинуты по фазе на 90º, так что квадратную скобку в (5.11) можно записать в виде 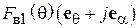 . Это означает, что поле антенны 1 имеет левую круговую поляризацию (если смотреть по направлению распространения волны). В то же время для поля антенны 2 та же скобка записывается как
. Это означает, что поле антенны 1 имеет левую круговую поляризацию (если смотреть по направлению распространения волны). В то же время для поля антенны 2 та же скобка записывается как 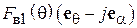 , т. е. это поле с правой круговой поляризацией.
, т. е. это поле с правой круговой поляризацией.
5.4. Интерференция полей антенны и ее зеркального изображения
Складывая выражения (5.11) и (5.13), получим
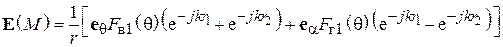 . (5.14)
. (5.14)
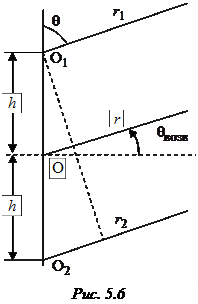 В выражении (5.14) следует учесть, что расстояния
В выражении (5.14) следует учесть, что расстояния  и
и  в дальней зоне из-за параллельности лучей О1М и О2М (рис. 5.5) могут быть представлены в виде
в дальней зоне из-за параллельности лучей О1М и О2М (рис. 5.5) могут быть представлены в виде 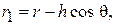
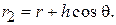 Далее вместо угла места сферической системы координат
Далее вместо угла места сферической системы координат 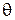 будет использоваться угол возвышения
будет использоваться угол возвышения 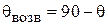 (рис. 5.6). Тогда получим
(рис. 5.6). Тогда получим
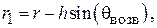
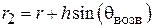 . (5.15)
. (5.15)
В этом случае
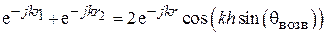 ,
,
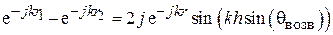 . (5.16)
. (5.16)
С учетом (5.14) и (5.16) окончательное выражение для поля в точке М примет вид
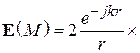
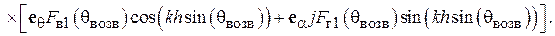 (5.17)
(5.17)
Векторная функция в квадратных скобках (5.17) называется характеристикой направленности антенны, поднятой над идеально проводящей поверхностью. Заметим сразу, что проводящая плоскость может существенно изменить поляризационные свойства поля антенны. Пусть, например, 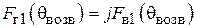 , т. е. поле антенны 1 имеет круговую поляризацию. Тогда выражение для суммарного поля излучения поля в точке наблюдения М (см. рис. 5.5) примет вид:
, т. е. поле антенны 1 имеет круговую поляризацию. Тогда выражение для суммарного поля излучения поля в точке наблюдения М (см. рис. 5.5) примет вид:
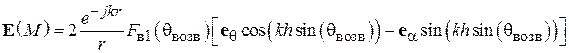 .
.
Как видно,  -я и
-я и 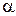 -я компоненты поля
-я компоненты поля 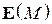 находятся либо в фазе (при одинаковых знаках обеих компонент), либо в противофазе (при противоположных знаках). В обоих случаях это линейная поляризация. При этом с изменением угла
находятся либо в фазе (при одинаковых знаках обеих компонент), либо в противофазе (при противоположных знаках). В обоих случаях это линейная поляризация. При этом с изменением угла  соотношение
соотношение 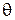 -й и
-й и  -й компонент изменяется, так что изменяется и ориентация линейно поляризованного вектора электрического поля.
-й компонент изменяется, так что изменяется и ориентация линейно поляризованного вектора электрического поля.
5.5. Частные случаи
Вертикальный диполь Герца создает, как известно, вертикально поляризованное электрическое поле.
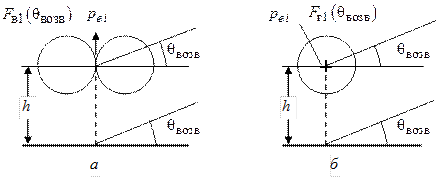
Рис. 5.7
При этом 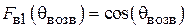 (рис. 5.7, а), так что диаграмма направленности диполя над проводящей поверхностью:
(рис. 5.7, а), так что диаграмма направленности диполя над проводящей поверхностью:
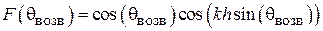 . (5.18)
. (5.18)
Такой же диполь, расположенный горизонтально (рис. 5.7, б), в плоскости, проходящей через центр диполя перпендикулярно его моменту, создает горизонтально поляризованное поле, причем ДН не зависит от угла 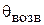 . Следовательно,
. Следовательно,
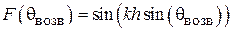 . (5.19)
. (5.19)
Для полуволнового вибратора, при его вертикальной ориентации, учитывая (5.18), получим
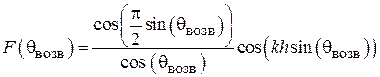 .
.
Для горизонтального вибратора  , так что выражение для
, так что выражение для 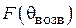 совпадает с (5.19).
совпадает с (5.19).
5.6. Интерференционные множители
Как видно из (5.18), (5.19), интерференция полей антенны и ее зеркального изображения учитывается интерференционными множителями 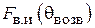 и
и 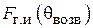 :
:
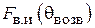
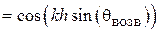 ,
, 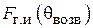
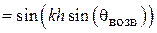 . (5.20)
. (5.20)
Параметром обеих этих функций является электрическая высота подъема антенны 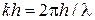 , однако, независимо от
, однако, независимо от 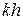 по горизонтали (в направлении
по горизонтали (в направлении 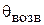 = 0 ) значения интерференционных множителей таковы:
= 0 ) значения интерференционных множителей таковы:
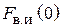 = 1,
= 1, 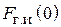 = 0,
= 0,
т. е. интерференционный множитель 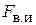 имеет в этом направлении максимум, а
имеет в этом направлении максимум, а 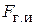 - нуль. При больших значениях
- нуль. При больших значениях 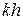 интерференционные множители представляют собой многолепестковые функции, причем с ростом
интерференционные множители представляют собой многолепестковые функции, причем с ростом 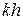 число лепестков растет. Несложно найти углы возвышения
число лепестков растет. Несложно найти углы возвышения 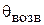 , при которых формируются максимумы и нули функций (5.20).
, при которых формируются максимумы и нули функций (5.20).
Множитель 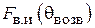 : максимумы - при
: максимумы - при 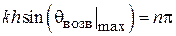 ; нули - при
; нули - при 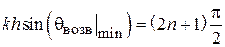 ; откуда
; откуда
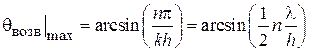 ,
,
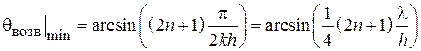 . (5.21)
. (5.21)
Множитель  : максимумы - при
: максимумы - при 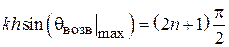 ; нули - при
; нули - при 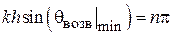 ; откуда
; откуда
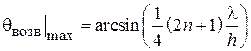 ,
,
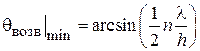 . (5.22)
. (5.22)
Как видно из (5.21) и (5.22), в двух случаях формулы для  и
и 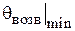 меняются местами.
меняются местами.
5.7. Экспериментальная установка
Лабораторный макет представляет собой передающую антенну в виде открытого конца прямоугольного волновода, который можно устанавливать на фиксированном расстоянии h от проводящей плоскости. Открытый конец волновода можно разворачивать на 90º вокруг его оси, реализуя тем самым антенну с вертикальной или горизонтальной поляризацией относительно проводящей плоскости, которая закреплена на стене. Приемная антенна помещена на раме, которую можно устанавливать под любым углом  к плоскости экрана и тем самым снимать диаграммы направленности системы «антенна – проводящая плоскость».
к плоскости экрана и тем самым снимать диаграммы направленности системы «антенна – проводящая плоскость».
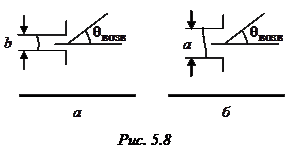 Диаграммы направленности открытого конца волновода можно приближенно рассчитать по формулам для прямоугольной излучающей площадки с размерами
Диаграммы направленности открытого конца волновода можно приближенно рассчитать по формулам для прямоугольной излучающей площадки с размерами 
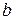 и косинусоидальным распределением электрического поля вдоль широкой стенки волновода.
и косинусоидальным распределением электрического поля вдоль широкой стенки волновода.
При установке антенны в положении, изображенном на рис. 5.8, а (вертикальная поляризация), ДН представляется выражением
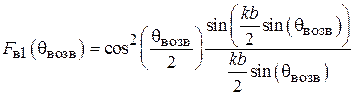 . (5.23)
. (5.23)
При установке волновода в положение, показанное на рис. 5.8, б (горизонтальная поляризация), ДН представляется формулой
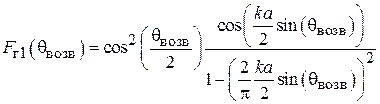 . (5.24)
. (5.24)
5.8. Проведение измерений
1. Включить генератор и измерительный усилитель. Генератор настроить на частоту, заданную преподавателем. Рассчитать соответствующую длину волны в свободном пространстве 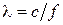 .
.
2. Установить одну из высот подъема излучателя, заданных преподавателем. Здесь следует учесть, что по шкале отсчет ведется от фланца излучателя. Для определения расстояния до центра излучателя к отсчету по шкале нужно прибавить 21 мм.
3. Установить излучатель в положение, при котором он создает излучение с вертикальной поляризацией относительно проводящей плоскости (широкая стенка волновода параллельна поверхности земли). В соответствующем положении должна быть и приемная антенна.
3. Снять диаграмму направленности 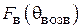 , особо фиксируя те углы, при которых наблюдаются нули и максимумы. Следует помнить при этом, что из-за квадратичности диода в индикаторном устройстве фактически снимается
, особо фиксируя те углы, при которых наблюдаются нули и максимумы. Следует помнить при этом, что из-за квадратичности диода в индикаторном устройстве фактически снимается 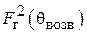 .
.
4. Установить излучатель в положение, когда он создает излучение с горизонтальной поляризацией. Измерить 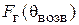 .
.
5. Повторить те же измерения для двух других высот h, заданных преподавателем.
5.9. Обработка результатов и теоретические расчеты
1. Шесть снятых диаграмм направленности нормировать к единице и построить их графики.
2. Для одной из высот подъема излучателя, исследованной экспериментально, рассчитать теоретические ДН. Высота задается преподавателем. Расчеты целесообразно выполнить в такой последовательности:
а) сначала рассчитать диаграммы 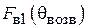 и
и 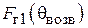 для открытого конца волновода с размерами а = 23 мм, b = 10 мм по формулам (5.23, 5.24).
для открытого конца волновода с размерами а = 23 мм, b = 10 мм по формулам (5.23, 5.24).
б) рассчитать ДН антенны над проводящей поверхностью 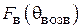 и
и 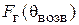 как произведение интерференционного множителя (5.20) на ДН излучателя (5.23) и (5.246).
как произведение интерференционного множителя (5.20) на ДН излучателя (5.23) и (5.246).
в) в расчеты нужно включить углы 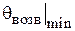 , при которых интерференционные множители равны 0, и
, при которых интерференционные множители равны 0, и 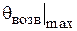 , при которых интерференционные множители равны 1 (формулы (5.21) и (5.22)).
, при которых интерференционные множители равны 1 (формулы (5.21) и (5.22)).
г) построить графики 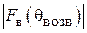 и
и 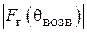 на тех же рисунках, что и экспериментальные ДН.
на тех же рисунках, что и экспериментальные ДН.
5.10. Контрольные вопросы
1. Приведите примеры использования метода зеркальных изображений в электростатике и покажите, что при правильном выборе знака заряда-изображения на всей плоскости S автоматически удовлетворяется граничное условие 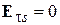 .
.
2. Какова связь между моментами диполей Герца, размещенных над проводящей плоскостью, и моментами их зеркальных изображений для вертикальных и горизонтальных диполей?
3. Покажите, что характеристики направленности антенны и ее зеркального изображения в случае вертикальной поляризации связаны соотношением 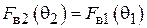 , причем
, причем 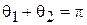 . Поясните эту связь рисунком.
. Поясните эту связь рисунком.
4. Покажите, что характеристики направленности антенны и ее зеркального изображения в случае горизонтальной поляризации связаны соотношением 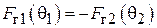 , причем
, причем 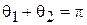 . Поясните эту связь рисунком.
. Поясните эту связь рисунком.
5. Покажите, что если антенна 1 создает в дальней зоне поле с круговой поляризацией, то антенна 2 (изображение) также создает поле, поляризованное по кругу, но с противоположным направлением вращения.
6. Постройте на качественном уровне диаграмму направленности вертикального диполя Герца, поднятого над проводящей поверхностью.
7. То же - для вертикального полуволнового электрического вибратора.
8. То же - для горизонтального диполя Герца.
9. То же - для горизонтального полуволнового электрического вибратора.
10. То же - для горизонтальной щелевой антенны.
11. То же - для вертикальной щелевой антенны.
12. Допустим, представлены аналитические выражения для интерференционных множителей. Как различить, какой из них относится к случаю вертикальной, а какой - горизонтальной поляризации?
13. Запишите выражения для интерференционных множителей в случае вертикальной и горизонтальной поляризаций. Выведите формулы для углов, соответствующих нулям и экстремумам этих множителей.
14. Как зависит число лепестков интерференционного множителя от высоты подъема антенны и от рабочей длины волны?
15. Как нужно ориентировать открытый конец волновода относительно проводящей поверхности, чтобы он создавал поле вертикальной (горизонтальной) поляризации?
16. Как нужно понимать рекомендацию о нормировании снятых диаграмм направленности? Что конкретно нужно сделать с экспериментальными результатами?
5.11. Содержание отчета
Отчет должен содержать:
1. Формулировку цели работу и краткие теоретические сведения.
2. Структурную схему экспериментальной установки.
3. Сведения о частоте, длине волны и высотах подъема излучателя.
4. Расчет длины волны в свободном пространстве.
5. Измеренные ДН излучателя 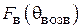 и
и 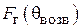 для 3 высот подъема.
для 3 высот подъема.
6. Расчетные ДН для вертикальной и горизонтальной поляризации излучаемого поля, построенные на одном графике с экспериментальными зависимостями.
8. Выводы.
6. ИССЛЕДОВАНИЕ МНОГОЭЛЕМЕНТНОЙ
АНТЕННОЙ РЕШЕТКИ «ВОЛНОВОЙ КАНАЛ»
Цели работы – экспериментальное исследование многоэлементных антенных решеток «волновой канал» и знакомство с методами расчета характеристик таких антенн
6.1. Общие сведения
Антенна «волновой канал» (ВК), известная также как антенна Уда–Яги (Uda–Yagi), широко используется в различных радиотехнических системах благодаря возможности получения высокой направленности при сравнительно простой и дешевой конструкции [8]–[10].
Антенны этого типа используются во многих частотных диапазонах, начиная от коротковолнового (рис. 6.1, а) до печатных вариантов в СВЧ-диапазоне. Наиболее широкое применение ВК получили в диапазонах метровых и дециметровых волн для приема телевизионного сигнала (рис. 6.1, б).
Конструктивно антенна состоит из расположенных параллельно друг другу активного и нескольких пассивных вибраторов, размещенных на общей несущей – траверсе (рис. 6.2). В ВК мощность от генератора по фидерной линии подводится, как правило, лишь к одному элементу (активному), остальные (пассивные) возбуждаются благодаря сильной взаимной электромагнитной связи.

а б
Рис. 6.1
Пассивные элементы можно разделить на два типа: 1) директоры, расположенные в направлении формирования основного лепестка диаграммы направленности (ДН) антенны; 2) как правило, один рефлектор (отражатель), расположенный с противоположной стороны от активного элемента. В верхней части ДМВ-диапазона и в СВЧ-диапазоне рефлектор может быть выполнен в виде сплошного металлического экрана (рис. 6.2).
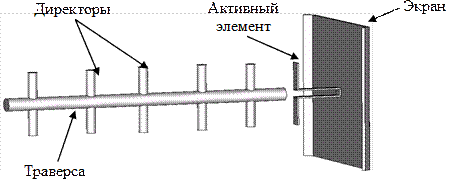
Рис. 6.2
Активный элемент выполняется в виде разрезного или петлевого вибратора с длиной около 0,5 λ (λ – длина волны в воздухе), длины директоров, как правило, на 5–15 % меньше активного. Расстояние между элементами антенны обычно не превосходит 0,35λ.
Для рефлектора, собственное сопротивление которого носит индуктивный характер, длина несколько больше 0,5 λ. При этом ток в рефлекторе опережает по фазе ток в активном вибраторе на 90°. В результате излучения активного вибратора и рефлектора в направлении главного лепестка ДН складывается в фазе, а в обратном направлении – в противофазе, что приводит к усилению излучения в направлении главного лепестка (в направлении директоров) и подавлению поля в противоположном направлении (в направлении рефлектора).
Аналогично рефлектору работают директоры, однако из-за емкостного характера их сопротивления (оно определяется их меньшей длиной) фаза тока в них отстает по фаз от тока в активном элементе.
Направленное осевое излучение формируется в результате создания амплитудно-фазового распределения в виде бегущей волны, распространяющейся от активного элемента в направлении директоров. На фазовое распределение существенное влияние оказывают размеры и взаимное расположение всех элементов. Выбор числа элементов антенны ВК осуществляется исходя из требуемого коэффициента усиления или ширины главного лепестка. Для больших ВК (при количестве элементов 15–20) дальнейшее наращивание числа элементов нецелесообразно, ввиду существенного замедления роста направленных свойств, обусловленного уменьшением амплитуды токов в дальних директорах.
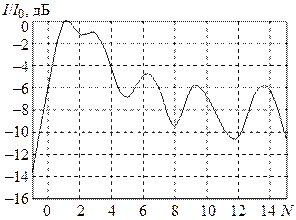
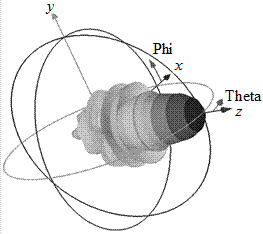
Рис. 6.3 Рис. 6.4
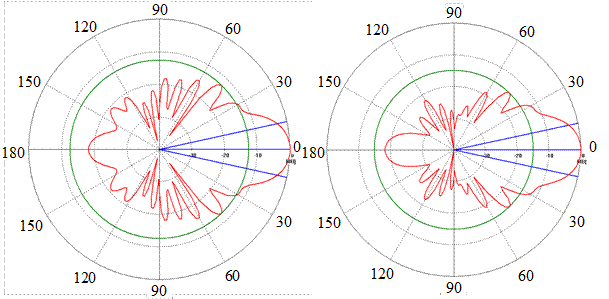
Рис. 6.5
Вклад каждого вибратора в полное поле излучения ВК определяется амплитудой тока, наведенного на элементе. На рис. 6.3 приводится распределение амплитуды тока по излучателям для 15-элементной антенны. Видно, что наиболее сильно возбуждаются два первых директора и активный вибратор.
В результате синфазного сложения полей в осевом направлении антенна имеет довольно узкий лепесток ДН. На рис. 6.4 приводится диаграмма направленности 15-элементной ВК, на рис. 6.5 ее сечения в Е- и Н-плоскостях.
6.2. Математическое описание вибраторных антенных решеток
Для проектирования антенных решеток и оптимизации их характеристик необходимо наличие точной и высокоэффективной в вычислительном отношении математической модели, поскольку многоэлементные ВК имеют большое число степеней свободы (длины вибраторов, расстояние между ними). Математическое описание можно свести к системе связанных интегральных уравнений относительно неизвестных функций распределения тока в каждом элементе.
6.2.1. Система связанных интегральных уравнений
для многоэлементной антенной решетки ВК
Математическая модель ВК сводится к системе связанных интегральных уравнений, порядок которой совпадает с количеством элемента. Например, для пятиэлементной антенны, представленной на рис. 6.6. искомыми являются пять функций распределения токов в рефлекторе, активном элементе и трех директорах.
Основываясь на тех же допущениях, что и при выводе уравнения Поклингтона одиночного вибратора (т. е. наличие сильного скин-эффекта, приближение тонкого провода) [1], можно сформулировать систему уравнений относительно неизвестных токов на каждом элементе ВК:
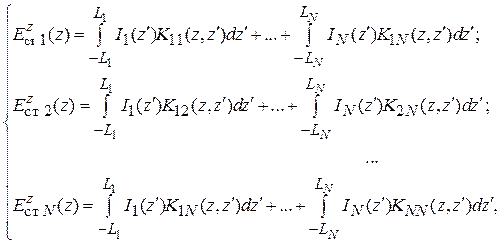 (6.1)
(6.1)
 где
где 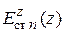 – стороннее электрическое поле (продольная компонента), создаваемое внешним источниками поля,
– стороннее электрическое поле (продольная компонента), создаваемое внешним источниками поля, 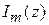 – ток, протекающий по оси m-го элемента. Ядра системы (6.1) определяются на основе соотношений:
– ток, протекающий по оси m-го элемента. Ядра системы (6.1) определяются на основе соотношений:
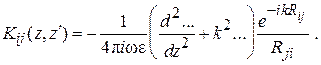 (6.2)
(6.2)
Здесь – 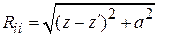 – расстояние между точкой интегрирования на оси и точкой наблюдения на поверхности i-го вибратора,
– расстояние между точкой интегрирования на оси и точкой наблюдения на поверхности i-го вибратора, 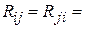
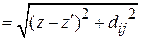 – расстояние между точкой интегрирования на оси i-го вибратора и точкой наблюдения на поверхности j-го вибратора, из (6.2) видно, что:
– расстояние между точкой интегрирования на оси i-го вибратора и точкой наблюдения на поверхности j-го вибратора, из (6.2) видно, что: 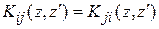 .
.
В случае одного активного элемента левые части системы уравнений (6.1) имеют вид:

Значения стороннего электрического поля во всех строчках системы, кроме второй, равняются нулю, что объясняется наличием возбуждающего источника лишь у второго элемента.
Физический смысл системы интегральных уравнений (6.1) заключается в том, что каждая строчка – это запись граничного условия для касательной компоненты электрического поля на поверхности вибратора. Интегралы в правой части любой строки системы (6.1) – это вклад в поле на поверхности одного из вибраторов от каждого из N элементов антенной решетки, таким образом, общее число интегралов в системе равно квадрату числа элементов решетки.
Полученная система (6.1) описывает в самосогласованной постановке систему из N вибраторов с учетом взаимного влияния их друг на друга. В частном случае, при отсутствии взаимной связи (например, в случае значительного междуэлементного расстояния, т. е. при  ), ядра системы (6.1) стремятся к нулю. Легко убедиться, что в этом случае система распадается на N независимых систем относительно тока в каждом уединенном вибраторе (т.е. на N независимых уравнений Поклингтона).
), ядра системы (6.1) стремятся к нулю. Легко убедиться, что в этом случае система распадается на N независимых систем относительно тока в каждом уединенном вибраторе (т.е. на N независимых уравнений Поклингтона).
6.2.2. Решение системы связанных ИУ
Система (6.1) является обобщением уравнения Поклингтона для одиночного элемента и решается в пять этапов:
1-й этап. Выбираем систему базисных функций 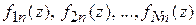 по которым раскладывается предполагаемое решение на первом, втором и
по которым раскладывается предполагаемое решение на первом, втором и
N-м вибраторах.
При этом возможна ситуация, в которой число базисных функций на каждом вибраторе неодинаково: 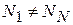 , а их вид на разных вибраторах разный. Получается система уравнений
, а их вид на разных вибраторах разный. Получается система уравнений
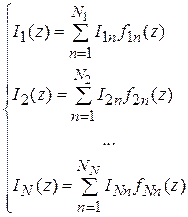 (6.3)
(6.3)
2-й этап. Подставляем разложение (6.3) в исходную систему интегральных уравнений (6.1) и, меняя порядок суммирования и интегрирования, получаем:
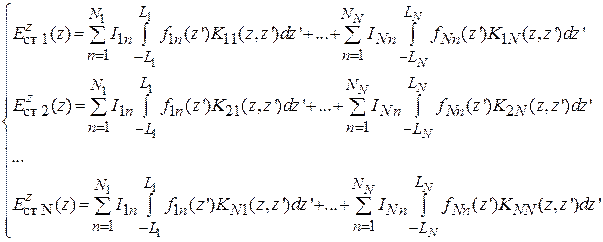
(6.4)
3-й этап. Формируем систему линейных алгебраических уравнений на основе метода Галеркина. На этом этапе конкретизируем и упростим ситуацию, будем считать, что ток на каждом вибраторе описывается тремя базисными функциями. Далее, последовательно умножив правую и левую части уравнений системы (6.4) на проекционные функции 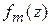 , получим систему линейных алгебраических уравнений (СЛАУ) M = 3N порядка относительно неизвестных базисных коэффициентов на каждом вибраторе:
, получим систему линейных алгебраических уравнений (СЛАУ) M = 3N порядка относительно неизвестных базисных коэффициентов на каждом вибраторе:
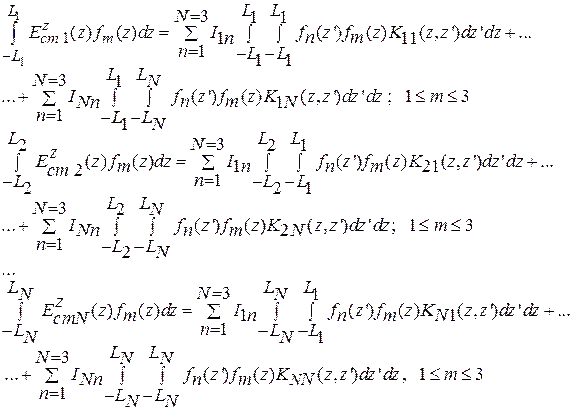 (6.5)
(6.5)
Систему (6.5) можно переписать в более наглядном виде, введя сквозную нумерацию базисных функций и токов:
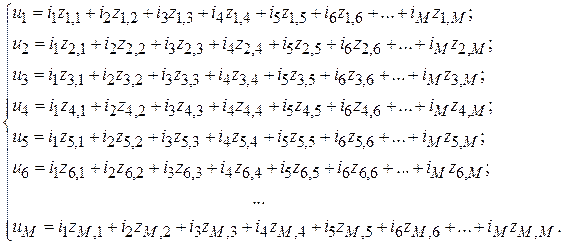 (6.6)
(6.6)
или в матричном виде – [U]=[Z][I]
Здесь 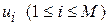 – амплитуды напряжения, выражаемые через интегралы от напряженности стороннего электрического поля:
– амплитуды напряжения, выражаемые через интегралы от напряженности стороннего электрического поля: 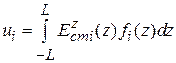 , причем вектор-столбец левых частей для ВК имеет вид
, причем вектор-столбец левых частей для ВК имеет вид
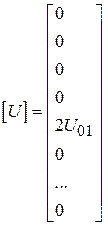 ,
,
где 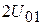 – напряжение дельта-источника, включенного в центре активного элемента (центральный сегмент активного элемента имеет 5-й порядковый номер), остальные элементы вектора [U] равны нулю; элементы матрицы [Z] – обобщенных взаимных импедансов
– напряжение дельта-источника, включенного в центре активного элемента (центральный сегмент активного элемента имеет 5-й порядковый номер), остальные элементы вектора [U] равны нулю; элементы матрицы [Z] – обобщенных взаимных импедансов 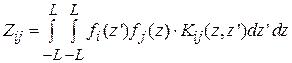 ; [I] – вектор неизвестных базисных коэффициентов.
; [I] – вектор неизвестных базисных коэффициентов.
4-й этап. Решаем систему уравнений (6.6) любым известным способом, например методом Гаусса. В результате решения будут найдены базисные коэффициенты токов.
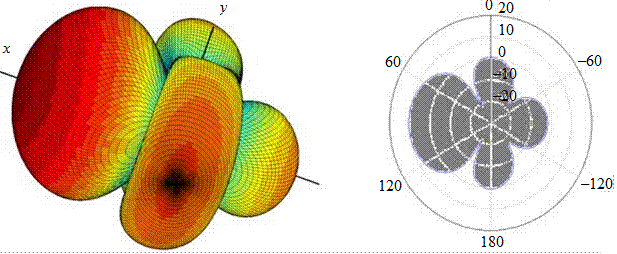
Рис. 6.7
5-й этап. По найденным коэффициентам на основе (6.3) восстанавливается ток в каждом вибраторе, затем находится входное сопротивление активного вибратора и ДН всей системы.
Результаты решения системы и вычисления ДН 5-элементной ВК (рис. 6.6) представлены на рис. 6.7.
Рассмотренный выше частный пример электродинамического анализа проволочных антенн можно легко алгоритмизировать в доступных математических пакетах.
|
|
Гораздо более удобной является реализация электродинамической модели в универсальных пакетах, специально разработанных для расчета характеристик проволочных структур достаточно общего вида. К таким пакетам относятся, прежде всего пакеты серии NEC, и их многочисленные вариации (winNEC, miniNEC, SuperNEC, MМANA).
6.2.3. Метод наведенных ЭДС
Как показывают расчеты и эксперимент, представление распределения тока по вибратору в виде зависимости 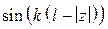 является достаточно точным, если он тонкий и близок к полуволновому. Метод учета излучения и взаимного влияния излучателей друг на друга при таком приближении получил название метода наведенных ЭДС.
является достаточно точным, если он тонкий и близок к полуволновому. Метод учета излучения и взаимного влияния излучателей друг на друга при таком приближении получил название метода наведенных ЭДС.
Если задать ток вдоль элементов АР в виде 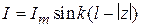 , где
, где 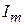 – неизвестный коэффициент тока на m-м вибраторе и подставить его в (6.5), то система интегральных уравнений сведется к системе линейных алгебраических уравнений и для пятиэлементной АР будет иметь вид
– неизвестный коэффициент тока на m-м вибраторе и подставить его в (6.5), то система интегральных уравнений сведется к системе линейных алгебраических уравнений и для пятиэлементной АР будет иметь вид
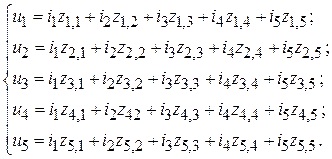 (6.7)
(6.7)
Интегралы в 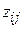 могут быть выражены через интегральный синус и косинуc. Для параллельных вибраторов одинаковой длины активная и реактивная составляющая равны соответственно [10]:
могут быть выражены через интегральный синус и косинуc. Для параллельных вибраторов одинаковой длины активная и реактивная составляющая равны соответственно [10]:
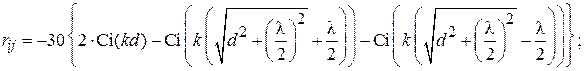
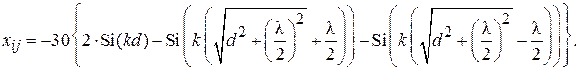
где d – расстояние между элементами; 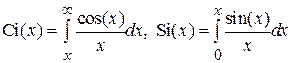 – интегральный косинус и синус. Графики зависимости
– интегральный косинус и синус. Графики зависимости  от расстояния приводятся в описании лабораторной работы №1.
от расстояния приводятся в описании лабораторной работы №1.
Элементы вектора-столбца левых частей для антенны ВК равны нулю, кроме элемента, относящегося к активному вибратору (элемент  ). В результате решения СЛАУ находятся значения амплитуд токов
). В результате решения СЛАУ находятся значения амплитуд токов  .
.
Приближенно диаграмма направленности ВК может быть оценена на основе теоремы перемножения ДН:
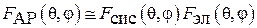 , (6.8)
, (6.8)
где 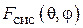 – множитель системы,
– множитель системы, 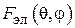 – диаграмма направленности одиночного элемента. Множитель системы определяется соотношением:
– диаграмма направленности одиночного элемента. Множитель системы определяется соотношением:
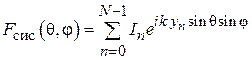 . (6.9)
. (6.9)
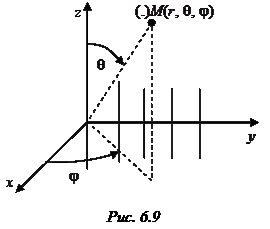 Здесь
Здесь 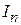 – найденные из СЛАУ амплитуды тока;
– найденные из СЛАУ амплитуды тока; 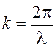 – волновое число свободного пространства; N – число элементов в решетке;
– волновое число свободного пространства; N – число элементов в решетке; 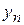 – координата n-го элемента, система координат в которой располагается ВК, изображена на рис. 6.9.
– координата n-го элемента, система координат в которой располагается ВК, изображена на рис. 6.9.
Диаграмма направленности элемента системы (полуволнового вибратора):
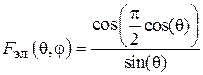 .
.
Приведенная методика является более простой, чем метод, основанный на решении системы ИУ. Точности расчета полевых характеристик оказывается достаточно для оценочных расчетов и экспресс-оценок. Такой подход к расчету полевых характеристик антенны реализован в программе «YAGIMAX». Основным недостатком метода является низкая точность при расчете входного сопротивления антенны.
6.3. Описание лабораторного макета
В зависимости от режима измерения в лабораторной работе используются две схемы. На рис. 6.10 представлен лабораторный макет для измерения частотной зависимости КСВ, на рис. 6.11 – схема, на основе которой проводятся исследования полевых характеристик (диаграмма направленности, коэффициент усиления и др.)
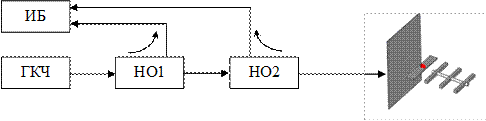
Рис. 6.10
Обе схемы содержат ГКЧ – генератор качающейся частоты, к выходу которого через направленные ответвители (НО1 и НО2) подключается испытуемая антенна. С выходов направленных ответвителей на индикаторный блок (ИБ) поступают сигналы, пропорциональные амплитуде падающей и отраженной волн, на основе которых рассчитывается КСВ или коэффициент отражения.
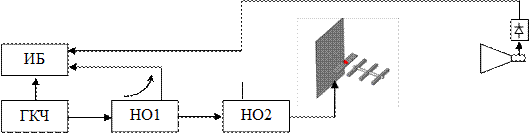
Рис. 6.11
При измерении полевых характеристик на индикаторный прибор поступает амплитуда волны, падающей на передающую антенну, и волны на приемном рупоре (измерительная рупорная антенна П6-23).
6.4. Задание и указания к выполнению работы
Программа работы:
1. Измерение КСВ ВК1 и ВК2 в полосе частот 2…3 ГГц.
2. Экспериментальное исследование ДН ВК1 в Е- и Н-плоскостях на заданных дискретных частотах из интервала 2.35…2.45 ГГц.
3. Расчет основных характеристик ВК на основе электродинамического моделирования в специализированных пакетах.
6.4.1. Измерение КСВ ВК1 и ВК2 в полосе частот 2…3 ГГц
Настройка измерительных приборов. Для измерения частотной зависимости КСВ собирается схема (рис. 6.10). Следует включить используемую аппаратуру и установить основные органы управления приборов в следующее состояние:
На блоке ИП Я2Р-67:
а) ручка «пределы» – 0 дБ;
б) «отсчет» – устанавливается на КСВ, соответствующий бесконечности;
в) «метка» – в крайнее правое положение;
г) кнопка «полоса» – широкая.
На блоке ГКЧ:
а) кнопка М1– нажата;
б) ручка «уровень» – в крайнее правое положение;
в) АМ – внутр.;
г) режим перестройки – F1, F2;
д) время перестройки – 0.08 с.;
е) ген. СВЧ – включен.
Калибровка прибора Я2Р-67. Перед измерениями следует провести калибровку прибора, которая выполняется следующим образом: кабель, соединяющий НО2 и антенну, отсоединяется от антенны, таким образом на его конце реализуется режим холостого хода, ручка «отсчет» – устанавливается на КСВ, соответствующий бесконечности, ручкой «калибровка» добиваются совмещения кривой частотной характеристики с отсчетной линией.
Процедура измерения КСВ. Частотную зависимость КСВ измеряют, устанавливая метку на заданную частоту (по цифровому индикатору) из рабочего диапазона и совмещая отсчетную прямую с кривой частотной зависимости в точке положения метки. При этом положение ручки «калибровка» в процессе измерений не меняется. Показания о значении КСВ снимаются со шкалы индикаторного блока в той точке, где остановился визир.
На частотной зависимости КСВ студенты должны определить те интервалы частот, где имеет место удовлетворительное согласование (совсем не обязательно, что на этих частотах будет и остронаправленное излучение) по критерию КСВ меньше или равно 2.0.
Измерения КСВ необходимо выполнить для ВК двух типов.
6.4.2. Экспериментальное исследование ДН ВК1 в Е- и в Н-плоскостях
на заданных дискретных частотах из интервала 2.35…2.45 ГГц
Настройка измерительных приборов. Для измерения ДН собирается схема, представленная на рис. 6.11. На канал «отр.» индикаторного блока подключается кабель от измерительной антенны (П6-23). Исследуемая антенна поворачивается по азимуту в направлении максимального сигнала (что соответствует наиболее высокому уровню кривой на приборе).
Калибровка прибора при снятии ДН. При установке исследуемой антенны в направлении главного максимума поставить визир с помощью ручки «калибр.» в положение 0 дБ.
Процедура измерения ДН. Выставить требуемую частоту метки, вращая антенну в азимутальной плоскости с шагом 5°, последовательно снимать показания по визиру, пользуясь ручками «отсчет» и переключателем «пределы». Выполнить аналогичное измерение для ВК 2.
Для одной из антенн необходимо измерить ДН в ортогональной плоскости, для этого поверните антенну вокруг траверсы на 90°.
6.4.3. Расчет основных характеристик ВК на основе
электродинамического моделирования в специализированных пакетах
Данный пункт выполняется по указанию преподавателя с помощью вспомогательного файла, созданного в программе MMANA, ядро которой основано на решении системы ИУ. Вспомогательный файл и программа MMANA находятся на ПК, установленном в лаборатории АФУ (ауд. 2233), путь к вспомогательному файлу C:\stud\yagi\model\15elem_yagi.mma, к программе C:\stud\yagi\mmana\mmana.rar.
Далее приводятся рекомендации по анализу антенны в пакете MMANA.
1. На вкладке Geometry отредактировать файл с геометрией антенны, выданный преподавателем и привести его в соответствие с экспериментальным образцом (рис. 6.12). Размеры директоров приводятся в табл. 6.1, 6.2, а площади экранов составляют 110x110 мм2. Далее необходимо задать центральную частоту анализа (в выпадающем меню Freq ввести 2400 МГц).
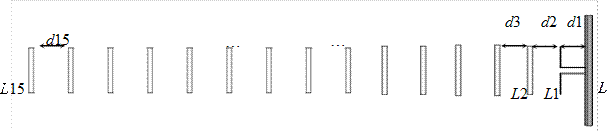
Рис. 6.12
Таблица 6.1
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| d, мм | 31,5 | 31 | 33 | 39,65 | 35,35 | 39 | 37,08 | 40,09 | |||||||
| L, мм | 49 | 49,3 | 51,4 | 51,4 | 49,3 | 46,3 | |||||||||
Таблица 6.2
| N | 1 | 2 | 3 | 4 | 5 | 6 |
| d, мм | 29 | 30,5 | 33 | 39,65 | 35,35 | 39 |
| L, мм | 49 | 49.3 | 51,4 | 51,4 | 49,3 | 49.3 |
2. Перейти к вкладке View и визуально оценить правильность редактирования геометрии.
3. Перейти к вкладке Compute, запустить расчет модели. При нажатии на кнопку Plot можно перейти в окно графических зависимостей, в нем задать диапазон анализа характеристик – 1000 МГц. Кнопка All points выводит зависимости на соответствующие вкладки: Z – действительная и мнимая составляющие входного импеданса антенны; SWR – КСВ (для правильного отображения которого необходимо выбрать пункт SWR- ON по правому щелчку мыши); Gain/ FB- коэффициент усиления и отношение вперед/назад. На вкладку Far Fields выводятся ДН антенны.
В результате расчета должны быть получены и помещены в отчет следующие зависимости:
1) КСВ в полосе частот;
2) диаграмма направленности в основных плоскостях на трех частотах (2.2, 2.4, 2.6 ГГц);
3) частотная зависимость коэффициента усиления и отношения вперед/назад.
Анализ необходимо выполнить для двух антенн ВК (ВК1 и ВК2).
6.5. Требования к содержанию отчета
Отчет должен содержать:
1. Формулировку цели работы.
2. Структурную схему установки в режиме измерения ДН и КСВ, геометрию антенны.
3. Измеренную зависимость КСВ для двух антенн.
4. Расчетную зависимость распределения токов на элементах решетки.
5. Измеренную ДН ВК 1 и ВК 2 в Е- и Н-плоскостях.
6. Расчетную ДН ВК1 и ВК 2 в Е- и Н-плоскостях на 3 частотах.
7. Расчетный КСВ в полосе частот.
8. Расчетную зависимость коэффициента усиления и отношения вперед/назад ВК.
9. Выводы, касающиеся зависимости характеристик ВК от геометрии и сравнительная оценка свойств ВК по отношению к антеннам других типов (рупорные, спиральные, полосковые).
6.6. Контрольные вопросы
1. Объяснить назначение конструктивных элементов ВК на рис. 6.1.
2. За счет чего в ВК происходит увеличение КУ по отношению к вибраторному излучателю?
3. Как увеличить КУ антенны ВК?
4. От чего зависит полоса рабочих частот антенны ВК?
5. Какую поляризацию э/м поля имеет ВК?
6. Объяснить суть метода наведенных ЭДС.
7. Возможна ли реализация двух линейных ортогональных поляризаций в антеннах этого типа?
8. Возможна ли реализация круговой поляризации (левой, правой) в антеннах ВК?
9. От чего зависит и как определяется отношение вперед/назад в ВК?
10. Можно ли уменьшить ширину основного лепестка ДН антенны в одной плоскости (например, в Н-плоскости), какими средствами?
11. Как изменятся характеристики антенны при увеличении толщины элементов?
12. Сравните электрические, конструктивные и климатические характеристики различных рефлекторов – вибратор, сплошной экран, сетчатый экран.
13. Каковы возможные способы повышения входного сопротивления активного вибратора?
14. В какой плоскости (E или H) ДН антенны ВК уже, почему?
15. Сформулируйте теорему перемножения ДН.
16. Изобразите качественно зависимость КУ антенны от числа элементов?
17. Дайте сравнительную оценку характеристик ВК и рупорного излучателя.
18. Существенное увеличение количества элементов для увеличения КНД неоправданно в связи со слабым их возбуждением. Предложите способ увеличения КНД на классе антенн ВК.
7. ИССЛЕДОВАНИЕ МИКРОПОЛОСКОВОЙ
АНТЕННОЙ РЕШЕТКИ
Цели работы – экспериментальное исследование характеристик простой 9-элементной МПАР: диаграммы направленности в основных сечениях, частотной зависимости КСВ на входе, уровне боковых лепестков, ширины главного лепестка ДН, а также теоретический расчет диаграммы направленности на основе упрощенной математической модели или с помощью стандартных универсальных пакетов программ.
7.1. Общие сведения
Микрополосковые (печатные) антенны (МПА) и микрополосковые антенные решетки (МПАР) в последнее время получили заметное распространение в массовых телекоммуникационных системах. Прежде всего это обусловлено их низкой стоимостью, высокой технологичностью, малой массой. Благодаря этим качествам МПАР в ряде случаев (прежде всего в тех радиосистемах, где не требуется высокий уровень излучаемой мощности и широкая полоса частот) успешно конкурируют с антенными решетками других типов – волноводными, волноводно-щелевыми, вибраторными и т. д. Существенным недостатком простейших однослойных МПАР, ограничивающим их применение, является узкая полоса рабочих частот.
Применяются МПА разнообразных форм, из которых наиболее распространенными являются прямоугольная (рис. 7.1, а – вид излучателя, б – распределение тока по излучателю) или дисковая (рис. 7.2). В большинстве случаев
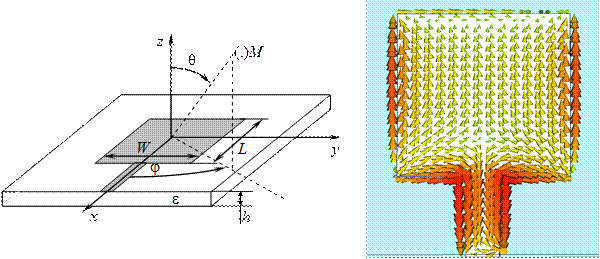
a б
Рис. 7.1
прямоугольная или дисковая МПА, имеющая одну точку питания, создает поле линейной поляризации. Это видно из картины распределения токов (рис. 7.1, б).
Для улучшения направленных свойств простейшие МПА объединяют в антенные решетки, примером является МПАР миллиметрового диапазона, выполненная по параллельной схеме питания (рис. 7.3).

Рис. 7.2 Рис. 7.3
 В данной лабораторной работе исследуются характеристики МПАР из девяти прямоугольных элементов, выполненной по параллельно-последовательной схеме (рис. 7.4).
В данной лабораторной работе исследуются характеристики МПАР из девяти прямоугольных элементов, выполненной по параллельно-последовательной схеме (рис. 7.4).
Представление о конструкции исследуемой МПАР дает фото на рис. 7.5. Материалом подложки является пенополиэтилен с относительной диэлектрической проницаемостью около единицы и толщиной 5 мм. Металлизация антенны (медь) нанесена на тонкий слой диэлектрического материала (стеклотекстолит с толщиной 0.2 мм) (рис. 7.5).

Рис. 7.5
Одиночные прямоугольные элементы МПАР имеют размер по узкой стороне около половины длины волны (с учетом замедления волны в диэлектрике подложки) и при питании подводящей микрополосковой линией с широкой стороны имеют довольно высокое входное сопротивление (около 160…300 Ом в зависимости от ширины элемента и электрической толщины подложки). При этом токи по элементу текут в направлении, параллельном узкой стенке (рис. 7.1, б), создавая в дальней зоне поле линейной поляризации.
Последовательное включение таких элементов через отрезок линии длиной около половины длины волны обеспечивает синфазное возбуждение всех излучателей. Для согласования входных сопротивлений трех последовательно соединенных элементов с питающей линией применен согласующий четвертьволновый трансформатор.
Три последовательные линейки включены параллельно, средняя линейка элементов имеет специально изогнутый отрезок линии, длина которого подобрана определенным образом с целью обеспечения синфазности токов в каждой линейке. Таким образом, все девять элементов данной МПАР возбуждены синфазно с амплитудным распределением, незначительно отличающимся от равномерного.
7.2. Математическое описание МПА
Математическое моделирование МПА следует выполнять на основе решения интегрального уравнения относительно двумерного распределения токов по плоскости антенны с ядром, зависящим от свойств материала подложки, такой подход является наиболее точным и реализован в ряде стандартных пакетов (MWOffice, Agilent и др.). Вместе с тем, существует ряд упрощенных подходов к расчету характеристик МПА, позволяющих с инженерной точностью оценить основные полевые характеристики. Одним из таких подходов является метод, разработанный Дернеридом, сводящийся к аналогии между МПА и отрезком длинной линии, нагруженным с двух сторон на резистивные и емкостные элементы. Резистивные элементы эквивалентны потерям на излучение, двух щелей с длиной равной ширине МПА W (рис. 7.1, а), расположенных на расстоянии равном длине элемента L, емкостные элементы описывают краевой эффект (емкость между концом полосковой линии передачи и проводящим основанием).
Резонансная частота  прямоугольной МПА зависит от геометрии антенны (прежде всего длины элемента L) и диэлектрической проницаемости подложки и определяется по формуле
прямоугольной МПА зависит от геометрии антенны (прежде всего длины элемента L) и диэлектрической проницаемости подложки и определяется по формуле 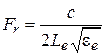 , где с – скорость света;
, где с – скорость света; 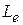 – эффективная длина излучателя;
– эффективная длина излучателя; 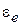 – эффективная диэлектрическая проницаемость, которая отличается от проницаемости материала подложки, поскольку поле МПА присутствует как в диэлектрике, так и в воздухе. Эти величины вычисляется по формулам:
– эффективная диэлектрическая проницаемость, которая отличается от проницаемости материала подложки, поскольку поле МПА присутствует как в диэлектрике, так и в воздухе. Эти величины вычисляется по формулам:
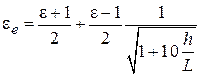 ;
;
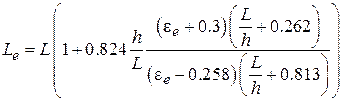 .
.
Здесь 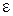 – диэлектрическая проницаемость материала подложки;
– диэлектрическая проницаемость материала подложки; 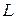 – длина элемента;
– длина элемента; 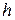 – толщина подложки.
– толщина подложки.
Увеличение диэлектрической проницаемости подложки при фиксированной геометрии элемента приводит к понижению резонансной частоты. В ряде случаев в целях уменьшения габаритов антенных систем прибегают к использованию материалов подложки с относительной диэлектрической проницаемостью от 2 до 10. Одновременно с этим уменьшение размеров МПА ведет к сужению полосы рабочих частот и уменьшению КНД.
Диаграмма направленности МПА определяется как: 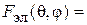
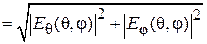 , где
, где  и
и  – угломестная и азимутальная компоненты поля излучения:
– угломестная и азимутальная компоненты поля излучения:
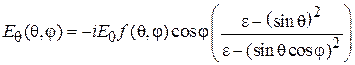 ;
;
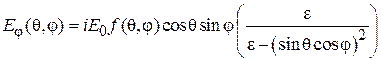 ;
;
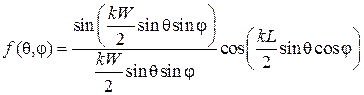 . (7.1)
. (7.1)
Здесь  – угол места и азимутальный угол сферической системы координат;
– угол места и азимутальный угол сферической системы координат; 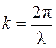 – волновое число;
– волновое число; 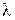 – длина волны в воздухе; W – ширина МПА;
– длина волны в воздухе; W – ширина МПА; 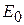 – постоянная, зависящая от амплитуды возбуждения.
– постоянная, зависящая от амплитуды возбуждения.
Диаграмма направленности антенной решетки вычисляется в соответствии с теоремой перемножения как произведение множителя системы 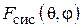 на ДН одного элемента
на ДН одного элемента 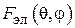 :
:
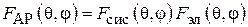 (7.2)
(7.2)
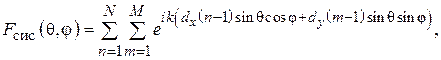 (7.3)
(7.3)
где  – число элементов в решетке по одной и другой координатам (в данном случае
– число элементов в решетке по одной и другой координатам (в данном случае  , общее число элементов в решетке равно произведению
, общее число элементов в решетке равно произведению  );
); 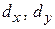 – периоды антенной решетки (т. е. расстояние между центрами элементов) по координатам х и у соответственно, для исследуемой в работе АР
– периоды антенной решетки (т. е. расстояние между центрами элементов) по координатам х и у соответственно, для исследуемой в работе АР 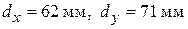 .
.
7.3. Лабораторный макет
В зависимости от режима измерения в лабораторной работе используются две схемы макета. На рис. 7.6. представлена схема лабораторного макета для измерения КСВ, на рис. 7.7, – схема, на основе которой проводятся исследования полевых характеристик.
Рис.7.6
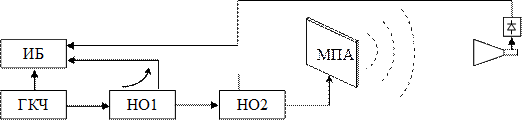
Рис. 7.7
Структура лабораторного макета аналогична используемой в работе № 6.
7.4. Программа работ
Основная программа:
1. Измерение КСВ МПАР в полосе частот 3.0…4.0 ГГц.
2. Экспериментальное исследование ДН МПАР.
3. Расчет ДН МПАР на основе приближенной модели.
Дополнительная программа:
1. Измерение отношения вперед/назад.
2. Измерение ДН по кроссполяризационному излучению.
3. Расчет основных характеристик МПАР на основе моделирования в специализированном пакете.
7.4.1. Измерение КСВ МПАР в полосе частот 3.0…4.0 ГГц
Описание настройки, калибровки приборов, а так же процедуры измерения МПАР не отличается от описания работы № 6, следует отметить, что анализ необходимо проводить в диапазоне 3…4 ГГц.
7.4.2. Экспериментальное исследование ДН МПАР
Провести измерение ДН в Е- или в Н-плоскости на заданных дискретных частотах из интервала 3.3…4.0 ГГц (по заданию преподавателя), зарегистрировать уровень боковых лепестков (УБЛ) и ширину главного лепестка.
7.4.3. Расчет ДН МПАР на основе приближенной модели
Настоящий пункт выполняется на основе математической модели, приведенной в разд. 7.2.
Исходные данные к расчету:
1. Размеры одиночного элемента 31×46 мм.
2. Период в Е-плоскости 62 мм.
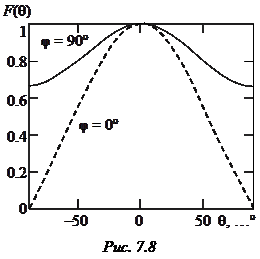 3. Период в Н-плоскости 71 мм.
3. Период в Н-плоскости 71 мм.
4. Толщина диэлектрика 5 мм.
5. Относительная диэлектрическая проницаемость подложки – 1,05 (пенополиэтилен).
Ниже представлены результаты расчета ДН МПА и МПАР на основе приведенных в разд. 7.2 соотношений для синфазной равноамплитудной МПАР той же геометрии, что и исследуемая в данной работе МПАР, но выполненной на подложке с диэлектрической проницаемостью 3 на частоте 2.6 ГГц.
7.4.4. Измерение отношения «вперед/назад»
Для этого в режиме измерения ДН ориентировать МПАР на приемную рупорную антенну по максимуму излучения, затем, развернув исследуемую антенну строго на 180°, снять показания с индикаторного блока.
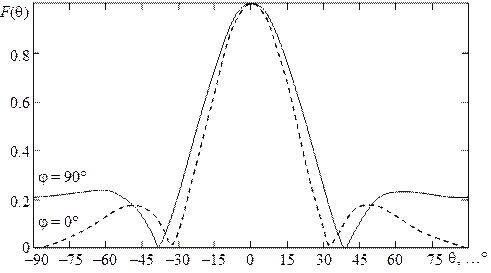
Рис. 7.9
7.4.5. Измерение ДН по кросс поляризации
(выполняется по указанию преподавателя)
В режиме измерения ДН следует развернуть приемную рупорную антенну вокруг своей продольной оси на 90°, затем снять угловую зависимость ДН аналогично п. 7.4.2.
Примечание: Следует иметь в виду, что при выполнении измерений ДН в некоторых направлениях уровень принимаемого сигнала может быть довольно низким (–15…–30 дБ по отношению к главному лепестку).
7.4.6. Расчет характеристик МПАР на основе моделирования
в специализированном пакете
Данный пункт выполняется по указанию преподавателя с помощью вспомогательного файла, который находится на ПК, установленном в лаборатории антенн (ауд. 2233), путь к вспомогательному файлу C:\stud\microstrip array\model\9el_array. В модели реализуется следующий подход: вначале проводится электродинамическое моделирование одиночного элемента АР, а затем схемотехническими средствами исследуется частотная зависимость входного КСВ всей МПАР.
7.5. Требования к содержанию отчета
Отчет должен содержать:
1. Формулировку цели работы.
2. Структурную схему установки в режиме измерения ДН и КСВ, геометрию исследуемой МПАР.
3. Результаты измерений частотной зависимости КСВ и ДН на нескольких частотах.
4. Расчетную (формулы (7.1)–(7.3)) ДН МПА и МПАР в Е- и Н-плоскости.
5. Отдельно следует привести расчетный и экспериментальный уровень боковых лепестков, ширину главного лепестка по уровню половинной мощности.
6. Выводы, касающиеся зависимости характеристик МПАР от ее архитектуры и сравнительной оценки свойств МПАР по отношению к антеннам других типов.
7.6. Контрольные вопросы
1. Объяснить назначение всех элементов топологии МПАР на рис. 7.5.
2. Сформулировать теорему перемножения ДН.
3. Как увеличить направленность МПАР в Е-плоскости?
4. Как увеличить направленность МПАР в Н-плоскости?
5. Как изменится ДН МПАР при увеличении числа элементов в каждой последовательной линейке?
6. Как изменится ДН МПАР при увеличении числа линеек?
7. Как увеличить направленность одного элемента?
8. Как изменятся характеристики МПА и МПАР при увеличении диэлектрической проницаемости подложки?
9. Какова ориентация вектора напряженности электрического поля в дальней зоне МПАР (рис. 7.5)?
10. Чем отличаются ДН исследуемой МПАР в Е- и Н-плоскостях?
11. От чего зависит УБЛ МПАР?
12. Как изменится форма ДН МПАР при увеличении периода МПАР?
13. Как надо изменить конструкцию данной МПАР, чтобы сузить главный лепесток ДН в Н-плоскости вдвое?
14. Как надо изменить конструкцию данной МПАР, чтобы перестроить ее МПАР на другую частоту?
15. Как будет изменяться форма ДН данной МПАР при изменении частоты?
16. Если выполнить МПАР при той же топологии на подложке из электрически более плотного материала, что изменится в ее характеристиках?
17. В чем состоит назначение трансформирующих элементов в каждой линейке данной МПАР?
18. Какие геометрические параметры МПА влияют на его рабочую частоту?
19. Случайно оборвалась одна дорожка (МП-линия), питающая центральную линейку данной МПАР, как изменятся характеристики всей МПАР?
20. Предложите другую геометрию МПАР при том же числе элементов.
21. Дайте сравнительную оценку характеристик МПАР и зеркальной антенны той же площади.
22. Сравните КУ данной МПАР и рупорной антенны с таким же раскрывом.
Список литературы
1. Марков Г. Т., Сазонов Д. М. Антенны: учебник для студентов радиотехнических специальностей вузов. Изд. 2-е, перераб. и доп. М.: Энергия, 1975.
2. Сугак М. И. Основы автоматизированного проектирования антенн: конспект лекций. Учебное электронное издание. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2011.
3. Brian C. Wadell. Transmission line design handbook, 1991, Artech House Inc.
4. Устройства СВЧ и антенны / Д. И. Воскресенский, В. Л. Гостюхин, В. М. Максимов, Л. И. Пономарев. M.: Радиотехника, 2008.
5. Кочержевский Г. Н., Ерохин Г. А., .Козырев Н. Д. Антенно-фидерные устройства: учебник для вузов. М.: Радио и связь, 1989.
6. Янке Е., Эмде Ф., Леш Ф. Специальные функции. М.: Наука, 1977.
7. Жук М. С., Молочков Ю. Б. Проектирование антенно-фидерных устройств. М.: Энергия, 1966.
8. Устройства СВЧ и антенны / Д. И. Воскресенский, В. Л. Гостюхин, В. М. Максимов, Л. И. Пономарев: под ред. Д. И. Воскресенского. Изд. 2-е, доп. и перераб. М.: Радиотехника, 2006.
9. Ротхаммель К. Антенны / пер. с нем. 3-е изд., доп. М.: Энергия, 1979.
10. Щелкунов С., Фриис Г. Антенны. Теория и практика. М.: Сов. радио, 1955.
11. Электродинамический расчет излучения полосковых антенн / Б. А. Панченко, С. Т. Князев, Ю. Б. Нечаев и др. М.: Радио и связь, 2002.
12. Панченко Б. А., Нефедов Е. И. Микрополосковые антенны. М.: Радио и связь, 1986.
Оглавление
1. АНТЕННАЯ СИСТЕМА ИЗ АКТИВНОГО И ПАССИВНОГО ВИБРАТОРОВ.. 3
1.1. Введение, теоретические сведения. 3
1.2. Экспериментальная установка. 7
1.3. Лабораторный эксперимент. 8
1.4. Контрольные вопросы.. 9
1.5. Содержание отчета. 10
2. ИССЛЕДОВАНИЕ СПИРАЛЬНОЙ АНТЕННЫ... 10
2.1. Введение. Теоретические сведения. 10
2.2. Экспериментальная установка. 14
2.3. Проведение измерений. 15
2.4. Контрольные вопросы.. 16
2.5. Содержание отчета. 16
3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ РУПОРНОЙ АНТЕННЫ... 17
3.1. Теоретические сведения. 17
3.2. Методика измерения коэффициента усиления антенны.. 25
3.3. Лабораторный макет. 30
3.4. Проведение измерений. 31
3.5. Обработка результатов измерений. 32
3.6.Контрольные вопросы.. 32
3.7. Содержание отчёта. 33
4. ИССЛЕДОВАНИЕ ЗЕРКАЛЬНОЙ АНТЕННЫ... 34
4.1. Введение. Принцип действия зеркальной антенны.. 34
4.2. Теоретические сведения. 35
4.2. Экспериментальная установка. 47
4.3. Эксперимент. 47
4.4. Обработка результатов эксперимента. 47
4.5.Контрольные вопросы.. 48
4.6.Содержание отчета. 50
5. ВЛИЯНИЕ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ НА ДИАГРАММЫ
НАПРАВЛЕННОСТИ АНТЕНН.. 50
5.1. Идея метода зеркальных изображений. 51
5.2. Применение метода зеркальных изображений к антеннам, размещенным над проводящей плоскостью.. 52
5.3. Обобщение на антенны с произвольно поляризованным излучением.. 55
5.4. Интерференция полей антенны и ее зеркального изображения. 56
5.5. Частные случаи. 57
5.6. Интерференционные множители. 58
5.7. Экспериментальная установка. 59
5.8. Проведение измерений. 59
5.9. Обработка результатов и теоретические расчеты.. 60
5.10. Контрольные вопросы.. 61
5.11. Содержание отчета. 62
6. ИССЛЕДОВАНИЕ МНОГОЭЛЕМЕНТНОЙ АНТЕННОЙ РЕШЕТКИ
«ВОЛНОВОЙ КАНАЛ». 62
6.1. Общие сведения. 62
6.2. Математическое описание вибраторных антенных решеток. 65
6.2.1. Система связанных интегральных уравнений для многоэлементной
антенной решетки ВК.. 65
6.2.2. Решение системы связанных ИУ.. 67
6.2.3. Метод наведенных ЭДС.. 70
6.3. Описание лабораторного макета. 72
6.4. Задание и указания к выполнению работы.. 72
6.4.1. Измерение КСВ ВК1 и ВК2 в полосе частот 2…3 ГГц. 73
6.4.2. Экспериментальное исследование ДН ВК1 в Е- и в Н-плоскостях
на заданных дискретных частотах из интервала 2.35…2.45 ГГц. 74
6.4.3. Расчет основных характеристик ВК на основе электродинамического
моделирования в специализированных пакетах. 74
6.5. Требования к содержанию отчета. 75
6.6. Контрольные вопросы.. 76
7. ИССЛЕДОВАНИЕ МИКРОПОЛОСКОВОЙ АНТЕННОЙ РЕШЕТКИ.. 77
7.1. Общие сведения. 77
7.2. Математическое описание МПА.. 79
7.3. Лабораторный макет. 81
7.4. Программа работ. 82
7.4.1. Измерение КСВ МПАР в полосе частот 3.0…4.0 ГГц. 82
7.4.2. Экспериментальное исследование ДН МПАР. 82
7.4.3 . Расчет ДН МПАР на основе приближенной модели. 82
7.4.4. Измерение отношения «вперед/назад». 83
7.4.5. Измерение ДН по кросс поляризации
(выполняется по указанию преподавателя) 83
7.4.6. Расчет характеристик МПАР на основе моделирования
в специализированном пакете. 83
7.5. Требования к содержанию отчета. 84
7.6. Контрольные вопросы.. 84
Список литературы.. 85
Алексеев Вадим Сергеевич,
Балландович Святослав Владимирович,
Грачев Сергей Владиславович,
Костиков Григорий Александрович,
Наумов Кир Петрович,
Семенихин Игорь Николаевич,
Сугак Михаил Иванович
Антенны и распространение радиоволн
Лабораторный практикум
Редактор И. Б. Синишева
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Подписано в печать 00.00.14. Формат 60×84 1/16.
Бумага офсетная. Печать офсетная. Печ. л. 5,5.
Гарнитура «Times New Roman». Тираж экз. Заказ .
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Издательство СПбГЭТУ «ЛЭТИ»
 197376, С.-Петербург, ул. Проф. Попова, 5
197376, С.-Петербург, ул. Проф. Попова, 5








