Методические указания
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕКСТИЛЬНЫЙ
УНИВЕРСИТЕТ имени А.Н. КОСЫГИНА»
Учебно-методический комплекс
по специальности 150406
“Машины и агрегаты текстильной
и легкой промышленности”
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторных работ по дисциплине
“ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ”
Составитель проф. С.В. Лушников
МОСКВА 2009
УДК 621.0:004.42(075)
Лушников С.В. Методические указания к выполнению лабораторных работ по дисциплине « Основы автоматизированного проектирования». – М.: ГОУВПО “МГТУ им. А.Н. Косыгина”, 2009. – 51с.
Методические указания посвящены решению задач синтеза и анализа рычажных и кулачковых механизмов, а также исследованию их движения с использованием программной системы компьютерной математики Mathcad. Рассматриваются методы решения указанных выше задач, приемы программирования при организации циклов, решения систем линейных и нелинейных уравнений, дифференциальных уравнений и оптимизационных процедур. Методические указания содержат примеры использования программных блоков для решения типовых математических задач при синтезе и анализе механизмов.
Методические указания предназначены для студентов факультета машиноведения и управления качеством.
Илл. 34, список литературы – 2 наим.
Рецензенты: зав. лабораторией теории механизмов и структуры машин Института машиноведения РАН, профессор, д.т.н. В.А. Глазунов;
профессор кафедры проектирования текстильных машин, д.т. н. В.И. Терентьев.
Подготовлено к печати на кафедре теории механизмов приборов и машин
СОДЕРЖАНИЕ
Лабораторная работа 1. Синтез кривошипно-ползунного механизма по коэффициенту отношения средних скоростей прямого и обратного хода ползуна…………….4
Лабораторная работа 2. Кинематический анализ кривошипно-ползунного механизма….…………………………………………………………………………......……….10
Лабораторная работа 3. Синтез кривошипно-ползунного механизма методами интерполирования и квадратического приближения.…………………………………...14
Лабораторная работа 4. Синтез кривошипно-ползунного, прямолинейно-направляющего механизма методом оптимизации…………………………………....21
Лабораторная работа 5. Динамический анализ машинного агрегата ….....………....26
Лабораторная работа 6. Синтез и анализ кулачкового механизма......………………34
Лабораторная работа 7. Силовой анализ кривошипно-ползунного механизма.........40
Лабораторная работа 8. Исследование движения упругого толкателя в кулачковом механизме………………………………………………………………………………...45
Список литературы ...........................................................................................................51
Лабораторнаяработа 1
Синтез кривошипно-ползунного механизма по коэффициенту
отношения средних скоростей прямого и обратного хода ползуна
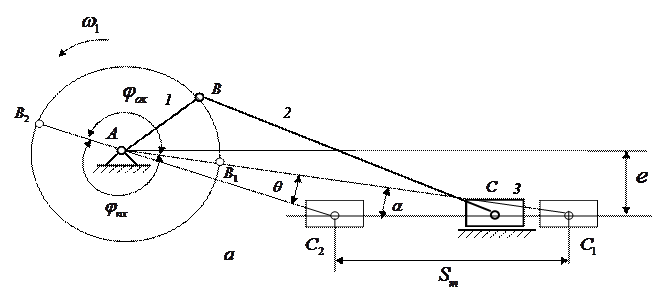
Синтез кривошипно-ползунного механизма (рис.1,а) по двум крайним положениям выходного звена 3(ползуна) при условии, что входное звено1 является кривошипом, часто встречается в практике проектирования механизмов. Если центр 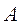 вращения кривошипа 1 расположен на линии, проходящей через точки
вращения кривошипа 1 расположен на линии, проходящей через точки 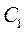 и
и 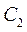 , определяющие крайние положения ползуна 3, линии
, определяющие крайние положения ползуна 3, линии 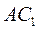 и
и 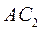 совпадают, а механизм называется аксиальным. Коэффициент изменения средней скорости прямого и обратного хода ползуна у такого механизма
совпадают, а механизм называется аксиальным. Коэффициент изменения средней скорости прямого и обратного хода ползуна у такого механизма 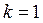 .
.
| |
У дезаксиального
механизма центр 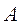 вращения кривошипа 1 смещен относительно линии
вращения кривошипа 1 смещен относительно линии 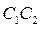 на
на
 |
величину эксцентриситета 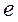 и этот коэффициент
и этот коэффициент 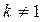 .
.
Коэффициент отношения средних скоростей обратного и прямого хода ползуна определяется по формуле
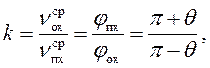 (1)
(1)
где 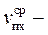 средняя скорость движения ползуна на стадии прямого хода,
средняя скорость движения ползуна на стадии прямого хода, 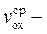 средняя скорость движения ползуна на стадии обратного хода.
средняя скорость движения ползуна на стадии обратного хода.
Из формулы (1) следует, что
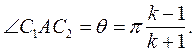 (2)
(2)
Синтез механизма с использованием системы линейных уравнений
Исходными параметрами для синтеза кривошипно-ползунного механизма являются: ход ползуна 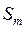 , коэффициент соотношения средних скоростей обратного и прямого хода ползуна
, коэффициент соотношения средних скоростей обратного и прямого хода ползуна 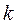 и угол давления
и угол давления 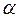 в крайнем правом положении ползуна. Расчет выполняется в прямоугольной системе координат
в крайнем правом положении ползуна. Расчет выполняется в прямоугольной системе координат 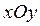 , центр которой (точка
, центр которой (точка 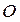 ) делит отрезок
) делит отрезок 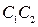 на две равные части. Уравнения прямых линий (рис.1,б), проходящих через точки
на две равные части. Уравнения прямых линий (рис.1,б), проходящих через точки 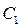 и
и 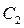 ,
,


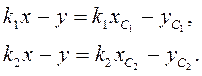 (3)
(3)
Расчетные формулы для определения коэффициентов системы линейных уравнений (3) имеют следующий вид:
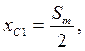
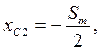
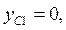
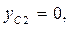 (4)
(4)
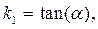
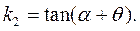
где 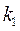 и
и 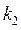 угловые коэффициенты уравнения прямых линий, проходящих соответственно через точки
угловые коэффициенты уравнения прямых линий, проходящих соответственно через точки 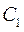 и
и 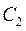 .
.
В результате решения системы уравнений (3) получаем координаты точки 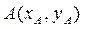 . Длина кривошипа
. Длина кривошипа 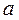 и длина шатуна
и длина шатуна 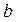 определяются по формулам
определяются по формулам
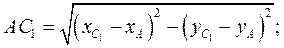
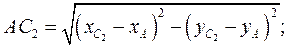

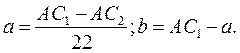 (5)
(5)
Эксцентриситет 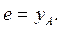
Для решения систем линейных уравнений (3) в Mathcad введена функция 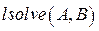 , которая определяет вектор
, которая определяет вектор 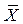 для системы линейных уравнений
для системы линейных уравнений 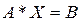 при заданной матрице коэффициентов
при заданной матрице коэффициентов 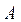 и векторе свободных членов
и векторе свободных членов 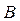 [1].
[1].
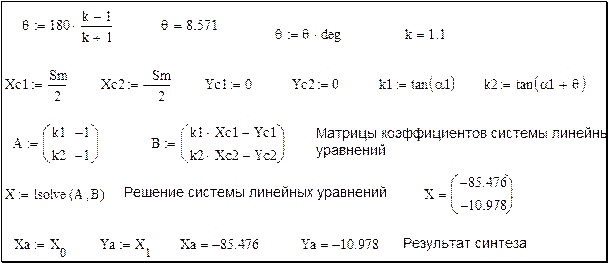
|
На рис.2 приведён фрагмент программы синтеза кривошипно-ползунного механизма по заданному коэффициенту производительности, в котором система двух линейных уравнений решается с помощью функции 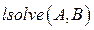 . В первой строчке программы вычисляются значения угла
. В первой строчке программы вычисляются значения угла 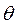 , где
, где 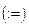 означает знак присвоения. Матрицы системы линейных уравнений записываются с помощью палитры знаков.
означает знак присвоения. Матрицы системы линейных уравнений записываются с помощью палитры знаков.
Синтез механизма с использованием нелинейных уравнений
Для вывода уравнений рассмотрим 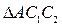 (рис.1,б), из которого следует
(рис.1,б), из которого следует
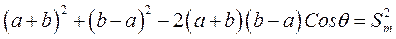 , (6)
, (6)
где ход ползуна 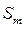 , угол
, угол 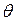 и один из размеров, например
и один из размеров, например 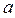 , являются известными параметрами. Определяется длина шатуна
, являются известными параметрами. Определяется длина шатуна 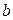 и эксцентриситет
и эксцентриситет 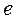 . Уравнение (6) является нелинейным уравнением, заданным в неявном виде, которое может быть решено численными методами. Приступая к решению уравнения, необходимо задать начальное значение искомого параметра
. Уравнение (6) является нелинейным уравнением, заданным в неявном виде, которое может быть решено численными методами. Приступая к решению уравнения, необходимо задать начальное значение искомого параметра 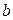 . Решение нелинейного уравнения в системе Mathcad [1] можно осуществить с помощью функции
. Решение нелинейного уравнения в системе Mathcad [1] можно осуществить с помощью функции 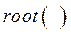 . На рис. 3,а показан фрагмент программы для синтеза кривошипно-ползунного механизма с решением одного нелинейного уравнения. В скобках функции
. На рис. 3,а показан фрагмент программы для синтеза кривошипно-ползунного механизма с решением одного нелинейного уравнения. В скобках функции 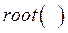 записывается имя
записывается имя
решаемого уравнения и символ того параметра, который определяется.
|

Эксцентриситет вычисляем по формулам
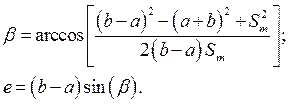 (7)
(7)
Система Mathcad позволяет проводить символьные преобразования, в частности из уравнения (6) можно получить выражение в явном виде для определения длины шатуна 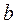 . Для этого необходимо выделить курсором переменную (рис.3,б), относительно которой решается уравнение, щелкнуть мышкой по опции
. Для этого необходимо выделить курсором переменную (рис.3,б), относительно которой решается уравнение, щелкнуть мышкой по опции 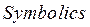 и далее в падающем меню указать на опции
и далее в падающем меню указать на опции 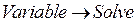
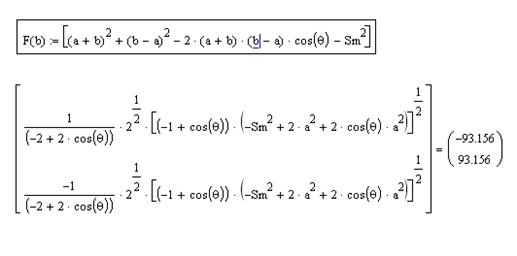
|
Если необходимо выполнить синтез механизма по трем параметрам 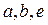 , решаем систему (8) нелинейных уравнений вместе с неравенством, которое ограничивает размер кривошипа
, решаем систему (8) нелинейных уравнений вместе с неравенством, которое ограничивает размер кривошипа 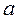 .
.
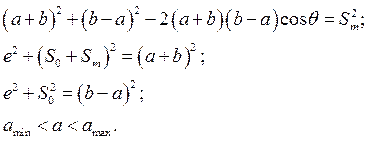 (8)
(8)
В этом случае исходными параметрами являются ход ползуна 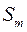 и угол
и угол 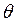 , а также
, а также 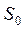 , расстояние между центром вращения кривошипа
, расстояние между центром вращения кривошипа 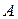 и крайним левым положением ползуна
и крайним левым положением ползуна 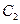 . Для решения системы (8) нелинейных уравнений используем функцию
. Для решения системы (8) нелинейных уравнений используем функцию 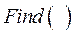 . Фрагмент программы с использованием этой функции показан на рис. 4. Для решения системы уравнений необходимо выполнить следующее:
. Фрагмент программы с использованием этой функции показан на рис. 4. Для решения системы уравнений необходимо выполнить следующее:

|
· задать начальные приближения для всех неизвестных параметров, входящих в систему уравнений;
· напечатать ключевое слово 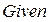 , которое указывает, что далее следует система уравнений;
, которое указывает, что далее следует система уравнений;
· ввести уравнения и неравенства, в которых используются логические знаки, в том числе и знак символического (логического) равенства;
· ввести функцию 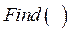 , в скобках которой указываются параметры, определяемые при решении системы уравнений;
, в скобках которой указываются параметры, определяемые при решении системы уравнений;
· результат решения системы присвоен столбцевой матрице 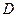 .
.
Mathcad решает уравнения с помощью итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению. При решении системы нелинейных уравнений Mathcad применяет итерационный метод Левенберга-Маркардта. Если результаты расчета требуется записать в файл данных – файлы ASCII, содержащие числовые данные, можно использовать функцию 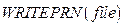 . В скобках указывается имя файла, в который записываются числовые значения. Каждая строка матрицы
. В скобках указывается имя файла, в который записываются числовые значения. Каждая строка матрицы 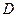 становится строкой в файле.
становится строкой в файле.
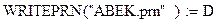
Для считывания структурированного файла данных применяем функцию 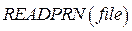 . Записывается следующим образом
. Записывается следующим образом
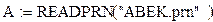 .
.
Результат считывания передаётся матрице 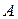 .
.
Лабораторная работа 2
Кинематический анализ кривошипно-ползунного механизма
 Кинематический анализ состоит в определении закона движения звеньев механизма по заданному движению входного звена. Основные задачи кинематического анализа: 1) определение положений звеньев и траекторий отдельных точек, 2) определение скоростей и ускорений звеньев и точек. При этом должны быть известны кинематическая схема механизма, размеры звеньев и закон движения входного звена. При кинематическом анализе кривошипно-ползунного механизма должны быть известны: длина кривошипа
Кинематический анализ состоит в определении закона движения звеньев механизма по заданному движению входного звена. Основные задачи кинематического анализа: 1) определение положений звеньев и траекторий отдельных точек, 2) определение скоростей и ускорений звеньев и точек. При этом должны быть известны кинематическая схема механизма, размеры звеньев и закон движения входного звена. При кинематическом анализе кривошипно-ползунного механизма должны быть известны: длина кривошипа 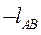 , длина шатуна
, длина шатуна 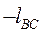 , величина эксцен-
, величина эксцен-
триситета 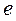 и угловая скорость кривошипа
и угловая скорость кривошипа 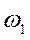 . Координаты точки
. Координаты точки 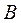
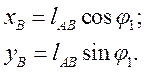 (9)
(9)
Координаты точки 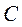
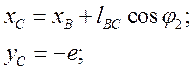 (10)
(10)
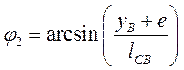 . (11)
. (11)
Формулы для определения скоростей точек и звеньев определяются в результате дифференцирования выражений (9), (10), (11) по времени 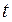 . В результате дифференцирования получаем
. В результате дифференцирования получаем
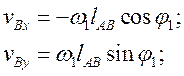
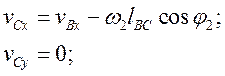 (12)
(12)
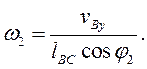
После повторного дифференцирования по времени получаем формулы для определения ускорений
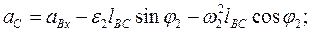 (13)
(13)
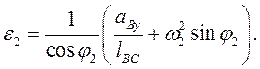
На рис.6 показан фрагмент программы, выполняющий кинематический анализ кривошипно-ползунного механизма. В начале фрагмента программы задается значение угловая
|
скорость кривошипа 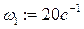 , указываются размеры кривошипа, шатуна, эксцентриситета, которые были определены в первой части программы синтеза механизма.
, указываются размеры кривошипа, шатуна, эксцентриситета, которые были определены в первой части программы синтеза механизма.

|
Для вычисления кинематических параметров механизма оформлена функция пользователя (вычислительный блок) с именем 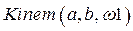 . В скобках указываются параметры, которые можно изменять при повторном использовании функции. Функция выделяется первой вертикальной чертой, расположенной сразу после имени функции и знака присвоения. Средства программирования сосредоточены в палитре программных элементов. В программе используется оператор цикла
. В скобках указываются параметры, которые можно изменять при повторном использовании функции. Функция выделяется первой вертикальной чертой, расположенной сразу после имени функции и знака присвоения. Средства программирования сосредоточены в палитре программных элементов. В программе используется оператор цикла 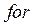 , организующий изменение угла поворота кривошипа
, организующий изменение угла поворота кривошипа 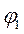 с шагом
с шагом 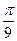 в пределах
в пределах 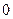 ...
...  . Цикл выделен второй вертикальной чертой. Знак присвоения внутри функции пользователя имеет вид стрелки
. Цикл выделен второй вертикальной чертой. Знак присвоения внутри функции пользователя имеет вид стрелки 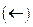 . В конце цикла осуществляется вывод результатов расчета из функции в виде матрицы. Матрица с результатами расчета имеет имя функции.
. В конце цикла осуществляется вывод результатов расчета из функции в виде матрицы. Матрица с результатами расчета имеет имя функции.
|

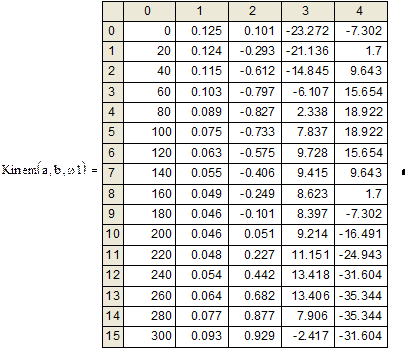
На рис.7 показана таблица с результатами расчета, а на рис.8 графики перемещения и скорости ползуна в функции угла поворота кривошипа. Для получения
таблицы с результатами расчета необходимо набрать имя функции и знак равенства 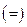 .
.
|
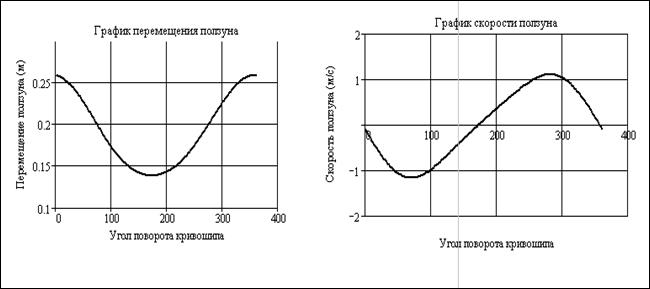
При построении графиков достаточно выполнить следующие действия:
· в панели математических знаков щелкните по кнопке с изображением графика – на экране появится палитра графиков;
· в палитре графиков щелкните на кнопке с изображением двумерного графика – на экране появится шаблон графика;
· введите вместо шаблона по горизонтальной и вертикальной осям графика имя функции с указанием номера столбца таблицы результатов.
Лабораторная работа 3
Синтез кривошипно-ползунного механизма методами интерполирования и квадратического приближения
При синтезе кривошипно-ползунного механизма (рис.9) по заданному закону движения 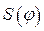 ползуна 3 в общем случае число неизвестных параметров механизма равно пяти [2].
ползуна 3 в общем случае число неизвестных параметров механизма равно пяти [2].
Функция перемещения ползуна имеет вид
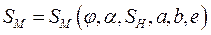 , (14)
, (14)
где 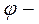 угол, определяющий положение входного звена 1;
угол, определяющий положение входного звена 1; 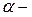 угол, определяющий начальное положение входного звена;
угол, определяющий начальное положение входного звена; 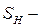 начальное положение ползуна 3;
начальное положение ползуна 3;
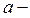 длина звена 1;
длина звена 1; 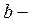 длина шатуна 2;
длина шатуна 2; 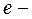 эксцентриситет.
эксцентриситет.
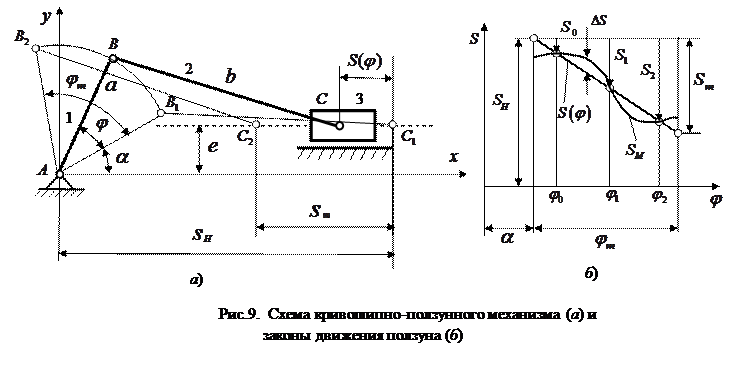
Необходимо спроектировать механизм, у которого отклонение 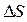 заданного закона движения ползуна
заданного закона движения ползуна 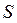 от закона, реализуемого механизмом
от закона, реализуемого механизмом 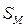 , было бы минимальным на всем интервале движения.
, было бы минимальным на всем интервале движения.
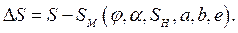 (15)
(15)
Для вывода уравнений, связывающих отклонение 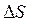 от заданного закона движения с размерами механизма, вводим в состав механизма дополнительное звено - кулисный камень 4 (рис.10) и получаем механизм с двумя степенями свободы. У этого механизма звенья 1 и 3 имеют возможность перемещаться по заданному закону движения, однако при этом длина
от заданного закона движения с размерами механизма, вводим в состав механизма дополнительное звено - кулисный камень 4 (рис.10) и получаем механизм с двумя степенями свободы. У этого механизма звенья 1 и 3 имеют возможность перемещаться по заданному закону движения, однако при этом длина 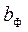 будет являться величиной переменной. Выражение (15) можно заменить разностью
будет являться величиной переменной. Выражение (15) можно заменить разностью
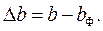 (16)
(16)
Для упрощения аналитического выражения, используемого при синтезе механизма, перейдем к взвешенной разности
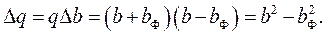 (17)
(17)
 |
Получаем аналитическое выражение взвешенной разности. Для этого проектируем замкнутый контур 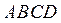 ,образованный звеньями механизма (рис.10), на координатные оси
,образованный звеньями механизма (рис.10), на координатные оси 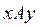
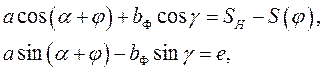 (18)
(18)
где 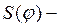 заданный закон движения ползуна 3.
заданный закон движения ползуна 3.
После преобразований уравнений (18) получаем выражение взвешенной разности
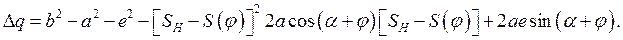 (19)
(19)
Далее считаем, что 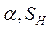 являются исходными, a
являются исходными, a 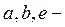 искомыми параметрами. В этом случае выражение взвешенной разности (19) приводится к обобщенному полиному вида
искомыми параметрами. В этом случае выражение взвешенной разности (19) приводится к обобщенному полиному вида
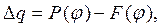
где 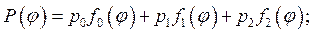

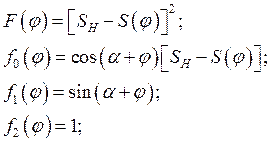
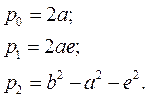
При синтезе методом интерполирования коэффициенты 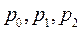 вычисляются из системы трех линейных уравнений (20), где каждое уравнение составлено для соответствующего узла интерполирования, а
вычисляются из системы трех линейных уравнений (20), где каждое уравнение составлено для соответствующего узла интерполирования, а 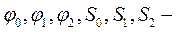 значения входной и выходной функций в узлах интерполирования
значения входной и выходной функций в узлах интерполирования
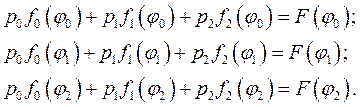 (20)
(20)
Затем определяем параметры
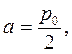
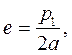
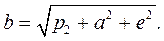
Недостаток метода интерполирования заключается в том, что между узлами интерполирования отклонение от заданной функции может быть большим, так как система уравнений (20) не накладывает никаких условий на отклонение от заданной функции между узлами интерполирования. Этот недостаток может быть устранен при квадратическом приближении функций, которое основано на обращении в минимум среднего квадратического отклонения от заданной функции
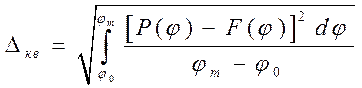 ,
,
где 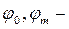 значения аргумента в начале и в конце отрезка приближения.
значения аргумента в начале и в конце отрезка приближения.
Среднее квадратическое отклонение становится минимальным, если обращается в минимум интеграл
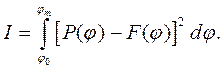 (21)
(21)
После преобразования выражения (21) получаем систему линейных уравнений
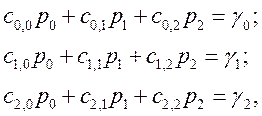 (22)
(22)
где коэффициенты системы линейных уравнений определяются по формулам
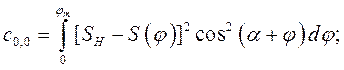
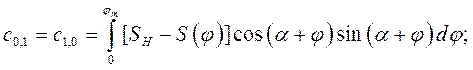
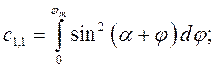
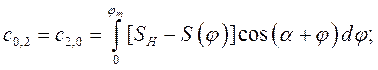
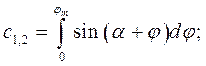
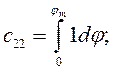
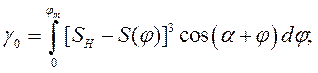
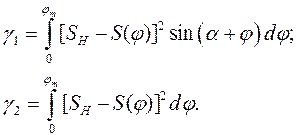
В качестве примера выполнен синтез кривошипноползунного механизма по заданному закону движения методом интерполирования при следующих исходных данных: 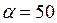 град.,
град., 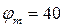 град.,
град., 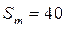 мм,
мм, 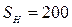 мм, закон движения линейный
мм, закон движения линейный
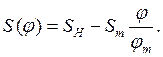 (23)
(23)
Результаты расчета: 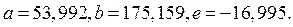 График отклонения от заданного закона движения
График отклонения от заданного закона движения 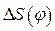 показан на рис.11 (кривая 1). Максимальное отклонение
показан на рис.11 (кривая 1). Максимальное отклонение 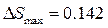 мм. Максимальный угол давления
мм. Максимальный угол давления 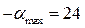 град.
град.
При тех же исходных данных выполнен синтез кривошипно-ползунного механизма методом квадратического приближения. Результаты расчета: 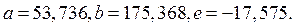
График отклонения 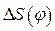 показан на рис.11 (кривая 2). Максимальное отклонение от заданного закона движения
показан на рис.11 (кривая 2). Максимальное отклонение от заданного закона движения 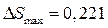 мм.
мм.
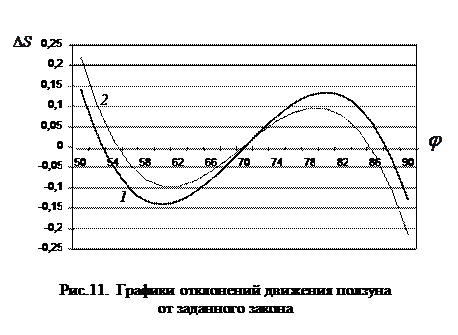 |
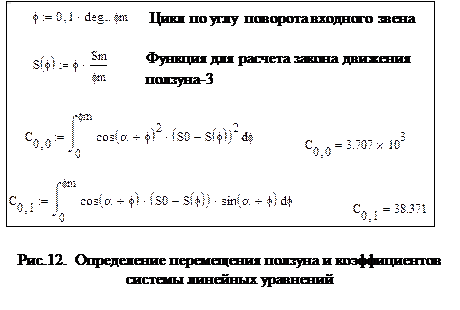 |
Как показали результаты расчета, максимальное отклонение 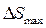 функции перемещения ползуна
функции перемещения ползуна 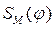 от заданной функции
от заданной функции 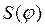 у механизма, полученного методом квадратического приближения, больше чем у механизма, рассчитанного по методу интерполирования. Однако следует иметь в виду, что участки с большим отклонением расположены на границах расчетного интервала. На рис.12 показан фрагмент программы синтеза кривошипно-ползунного механизма по заданному закону движения ползуна методом квадратического приближения. Показан цикл по углу
у механизма, полученного методом квадратического приближения, больше чем у механизма, рассчитанного по методу интерполирования. Однако следует иметь в виду, что участки с большим отклонением расположены на границах расчетного интервала. На рис.12 показан фрагмент программы синтеза кривошипно-ползунного механизма по заданному закону движения ползуна методом квадратического приближения. Показан цикл по углу 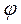 поворота входного звена, формула для расчета закона движения выходного звена и вычисление коэффициентов системы линейных уравнений с помощью оператора интегрирования. Оператор интегрирования используется для вычисления определенного интеграла функции по некоторому интервалу. Система Mathcad [1] численно оценивает определенные интегралы с помощью алгоритма Ромберга. Метод Ромберга ускоряет сходимость к интегралу метода трапеций или метода прямоугольников, экстраполируя последовательность оценок величины интеграла и ширины шага интегрирования. Для решения системы линейных уравнений используется функция
поворота входного звена, формула для расчета закона движения выходного звена и вычисление коэффициентов системы линейных уравнений с помощью оператора интегрирования. Оператор интегрирования используется для вычисления определенного интеграла функции по некоторому интервалу. Система Mathcad [1] численно оценивает определенные интегралы с помощью алгоритма Ромберга. Метод Ромберга ускоряет сходимость к интегралу метода трапеций или метода прямоугольников, экстраполируя последовательность оценок величины интеграла и ширины шага интегрирования. Для решения системы линейных уравнений используется функция 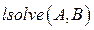
Лабораторная работа 4
Синтез кривошипно-ползунного, прямолинейно-направляющего механизма методом оптимизации
При синтезе кривошипно-ползунного направляющего механизма (рис.13) оптимизационными методами исходными данными для расчета являются:
 |
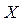 координата заданной прямой линии,
координата заданной прямой линии, 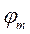 угол поворота кривошипа 1, определяющий продолжительность перемещения точки
угол поворота кривошипа 1, определяющий продолжительность перемещения точки 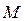 , расположенной на шатуне 2, по прямой линии. В результате синтеза необходимо определить параметры
, расположенной на шатуне 2, по прямой линии. В результате синтеза необходимо определить параметры 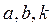 механизма, при которых траектория точки
механизма, при которых траектория точки 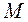 , на угле поворота
, на угле поворота 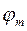 кривошипа незначительно отличается от заданной траектории (прямой линии). Целевая функция имеет вид
кривошипа незначительно отличается от заданной траектории (прямой линии). Целевая функция имеет вид
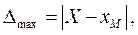 (24)
(24)
где 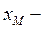 координата точки
координата точки 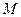 . Координаты точки
. Координаты точки 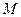 вычисляются по формулам
вычисляются по формулам
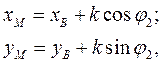
где угол 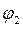 определяется по формуле (11).
определяется по формуле (11).
На размеры звеньев накладываются ограничения:
· - ограничения на максимальный и минимальный размеры звеньев 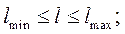
· - условие существования кривошипа 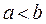 ;
;
· - условие, обеспечивающее требуемые углы передачи 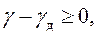
где 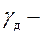 допускаемый угол передачи.
допускаемый угол передачи.
Оптимизационный синтез можно выполнить с помощью универсальной, программной математической системы Mathcad Pro [1], в которой для этих целей предусмотрена функция Minimize 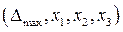 , реализующая метод нелинейной оптимизации Quasi-Newton. Функция Minimize
, реализующая метод нелинейной оптимизации Quasi-Newton. Функция Minimize 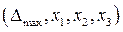 используется в составе блока решения, открываемого директивой Given. Внутри блока располагаются ограничения в виде неравенств. Предварительно, до директивы Given, необходимо задать начальное приближение варьируемых параметров
используется в составе блока решения, открываемого директивой Given. Внутри блока располагаются ограничения в виде неравенств. Предварительно, до директивы Given, необходимо задать начальное приближение варьируемых параметров 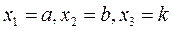 и расположить формулы, по которым вычисляется целевая функция
и расположить формулы, по которым вычисляется целевая функция 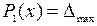 .
.
Порядок оформления программного блока:
· значения начального приближения;
· целевая функция;
· ключевое слово Given;
· ограничения;
· функция Minimize().
Ограничения вводятся с помощью булевых операторов.
На рис. 14 показан фрагмент программы, реализующий оптимизационный алгоритм определения размеров кривошипно-ползунного механизма. В этой программе
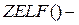 имя целевой функции, которая рассчитывается ранее.
имя целевой функции, которая рассчитывается ранее.
|
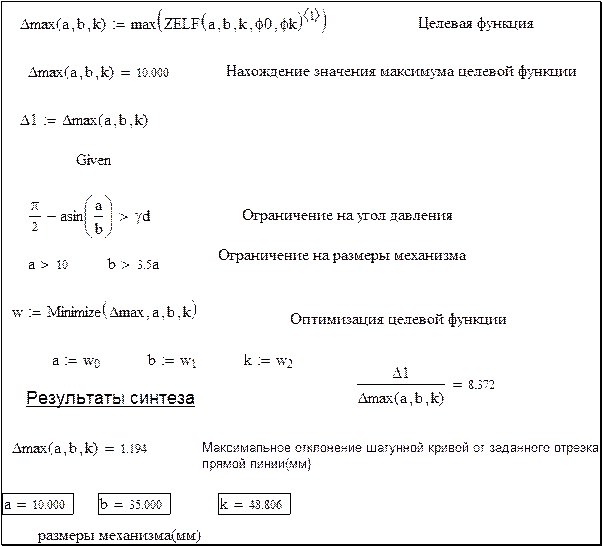
На рис.15 показан фрагмент программы, предназначенный для расчета схемы механизма и траектории точки 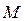 в прямоугольной системе координат. Эта схема используется для разработки анимации ( или “оживления”). В системе Mathcad для анимации используется стандартная технология создания анимационных файлов с расширением .avi и их воспроизведение с помощью программы Microsoft Video 1.1. В системе имеется встроенная переменная FRAME, принимающая целочисленные значения и идентифицирующая номер текущего кадра.
в прямоугольной системе координат. Эта схема используется для разработки анимации ( или “оживления”). В системе Mathcad для анимации используется стандартная технология создания анимационных файлов с расширением .avi и их воспроизведение с помощью программы Microsoft Video 1.1. В системе имеется встроенная переменная FRAME, принимающая целочисленные значения и идентифицирующая номер текущего кадра.

|
Любая функция, график которой планируется наблюдать в развитии, должна быть функцией этой переменной. Диапазон изменения переменной FRAME задается в диалоговом окне команды Animate (анимация) меню View(вид). Анимация осуществляется путем просмотра созданной последовательности кадров с помощью проигрывателя.
Для создания анимации (рис.16) необходимо выполнить следующие действия:
1. Войти в процедуру форматирования графика, отключить автоматический выбор масштаба графика (Autoscale) и установить предельные значения на осях графика вручную.
2.
|
Активизировать опцию Animate из пункта меню View. В открывшемся диалоговом окне (Animate) задается диапазон значений переменной FRAME и скорость следования кадров.
3. Не закрывая диалогового окна Animate, вернуться к документу и протяжкой мыши выделить график пунктирным контуром, тем самым указав системе объект анимации.
4. Вернуться в диалоговое окно Animate и нажать кнопку "Animate" для создания видеофайла. После создания видеофайла появится окно (Playback) видеопроигрывателя, на котором, после нажатия кнопки "Пуск ", можно наблюдать анимацию механизма. Готовую анимацию можно сохранить в формате .avi , нажав кнопку "Save as" в диалоговом окне Animate.
5. Просмотр файлов формата .avi осуществлять путем вызова видеопроигрывателя, для чего необходимо активизировать опцию Playback позиции View главного меню. Затем открыть файл и запустить анимацию.
Лабораторная работа 5
Динамический анализ машинного агрегата
Для определения закона движения входного звена по заданным силам, действующим на звенья механизма, используется уравнение, называемое уравнением движения механизма, которое может быть представлено в различной форме. Одна из наиболее простых форм получается на основании теоремы об изменении
 | |||
| |||
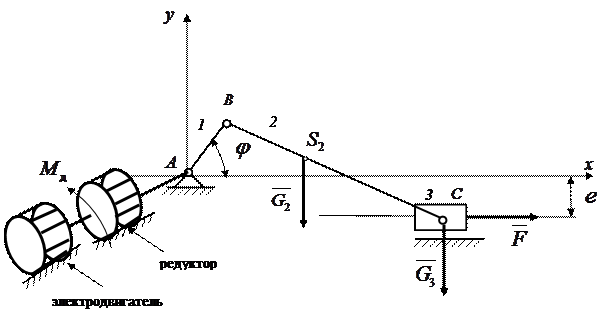
кинетической энергии. В некоторых случаях [2] удобно применять уравнение движения механизма, представленное в форме дифференциального уравнения второго порядка. В этой лабораторной работе необходимо разработать программу решения уравнения движения машинного агрегата (рис.17), в котором кривошипно-ползунный механизм приводится в движение от трехфазного, асинхронного электродвигателя переменного тока с короткозамкнутым ротором. Между электродвигателем и кривошипно-ползунным механизмом установлен редуктор. Механическая характеристика электродвигателя
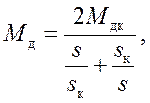
где 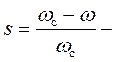 коэффициент скольжения ротора электродвигателя,
коэффициент скольжения ротора электродвигателя,
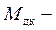 максимальный (критический) движущий момент,
максимальный (критический) движущий момент, 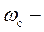 синхронная угловая скорость ротора электродвигателя,
синхронная угловая скорость ротора электродвигателя, 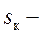 критический коэффициент скольжения.
критический коэффициент скольжения.
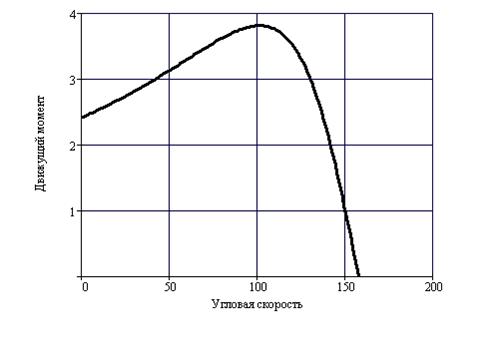
|
График движущего момента в зависимости от угловой скорости ротора электродвигателя показан на рис. 18.
В дифференциальной форме уравнение движения имеет вид
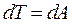 ,
,
где 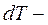 дифференциал кинетической энергии;
дифференциал кинетической энергии; 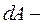 дифференциал работы.
дифференциал работы.
Кинетическая энергия звена приведения
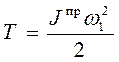 (25)
(25)
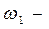 угловая скорость звена приведения,
угловая скорость звена приведения,
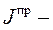 приведенный момент инерции машинного агрегата
приведенный момент инерции машинного агрегата
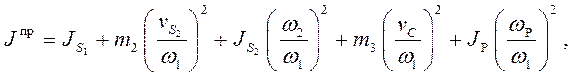
где 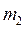 и
и 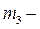 массы звеньев,
массы звеньев, 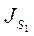 ,
, 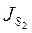 ,
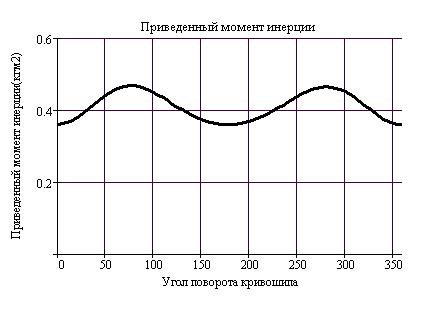
, 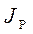 - моменты инерции звеньев механизма и ротора электродвигателя. График зависимости приведенного момента инерции от угла поворота кривошипа показан на рис.19
- моменты инерции звеньев механизма и ротора электродвигателя. График зависимости приведенного момента инерции от угла поворота кривошипа показан на рис.19
|
Дифференциал работы
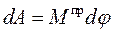 . (26)
. (26)
после преобразований получим нелинейное дифференциальное уравнение движения машинного агрегата
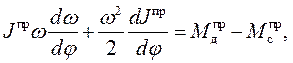 (27)
(27)
где
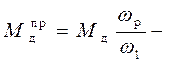 приведенный момент движущих сил,
приведенный момент движущих сил,
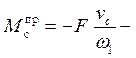 приведенный момент сил сопротивления (рис.20),
приведенный момент сил сопротивления (рис.20), 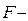 сила сопротивления, действующая на участке рабочего хода ползуна.
сила сопротивления, действующая на участке рабочего хода ползуна.
|
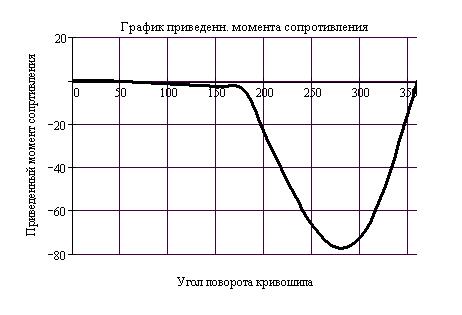
Угловое ускорение кривошипа определяется по формуле
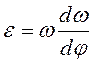 .
.
Для решения уравнения (27) численным методом запишем его в следующем виде
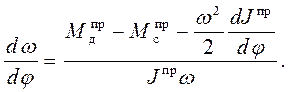 (28 )
(28 )
Производная от приведенного момента инерции машинного агрегата по углу поворота звена приведения 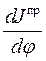 определяется численным методом. Для вычисления производной Mathcad Pro использует модифицированный метод Риддера. Согласно этому методу шаг дифференцирования подбирается таким, чтобы была обеспечена сходимость вычислительного процесса. Поэтому возникает необходимость в интерполяции функции приведенного момента инерции
определяется численным методом. Для вычисления производной Mathcad Pro использует модифицированный метод Риддера. Согласно этому методу шаг дифференцирования подбирается таким, чтобы была обеспечена сходимость вычислительного процесса. Поэтому возникает необходимость в интерполяции функции приведенного момента инерции 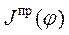 , полученной расчетным путем в отдельных узловых точках. Для этого можно воспользоваться функциями
, полученной расчетным путем в отдельных узловых точках. Для этого можно воспользоваться функциями 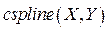 и
и 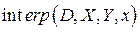 . Соответствующий фрагмент программы показан на рис.21.
. Соответствующий фрагмент программы показан на рис.21.
|

Функция 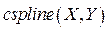 вычисляет вектор
вычисляет вектор 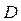 коэффициентов кубического сплайна с параболическим приближением в конечных точках. Функция
коэффициентов кубического сплайна с параболическим приближением в конечных точках. Функция 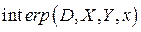 вычисляет значения функции
вычисляет значения функции 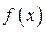 с использованием кубических сплайнов для произвольного значения аргумента
с использованием кубических сплайнов для произвольного значения аргумента 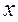 по предварительно определенному вектору
по предварительно определенному вектору 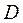 . Необходимо также выполнить интерполяцию функции приведенного момента сопротивления
. Необходимо также выполнить интерполяцию функции приведенного момента сопротивления 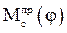 , что требуется для последующего выбора шага
, что требуется для последующего выбора шага 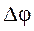 при решении уравнения движения машинного агрегата методом Рунге-Кутта четвертого порядка.
при решении уравнения движения машинного агрегата методом Рунге-Кутта четвертого порядка.
В систему Mathcad Pro [1] введена функция 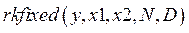 . Эта функция используется для решения дифференциального уравнения методом Рунге-Кутта четвертого порядка (рис.22). В скобках после имени функции указываются:
. Эта функция используется для решения дифференциального уравнения методом Рунге-Кутта четвертого порядка (рис.22). В скобках после имени функции указываются:
· 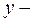 вектор начальных условий размерности
вектор начальных условий размерности 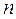 , где
, где 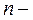 порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений), а для дифференциального уравнения первого порядка, как в нашем случае, вектор начальных значений вырождается в одну точку;
порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений), а для дифференциального уравнения первого порядка, как в нашем случае, вектор начальных значений вырождается в одну точку;
· 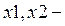 граничные точки интервала, на котором проводится поиск решения дифференциальных уравнений;
граничные точки интервала, на котором проводится поиск решения дифференциальных уравнений;
· 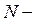 число точек (не считая начальной точки), в которых определяется приближенное решение, с его помощью определяется число строк
число точек (не считая начальной точки), в которых определяется приближенное решение, с его помощью определяется число строк 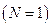 в матрице, возвращаемой функцией
в матрице, возвращаемой функцией 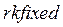 .
.
· 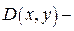 функция, возвращающая значение в виде вектора из
функция, возвращающая значение в виде вектора из 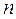 элементов, содержащих первые производные неизвестных функций.
элементов, содержащих первые производные неизвестных функций.
В результате решения получается матрица, имеющая два следующих столбца:
· первый столбец содержит точки, в которых ищется решение дифференциального уравнения;
· второй столбец содержит значения найденного решения в соответствующих точках, то-есть значения угловой скорости 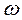 звена приведения.
звена приведения.
Перед решением дифференциального уравнения движения (27) необходимо задавать начальные условия. При решении уравнения на стадии разгона начальные условия
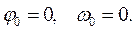 .
.
На стадии установившегося движения угловая скорость звена приведения в начале цикла неизвестно и её в первом приближении можно принять равной номинальному значению
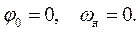
Если приведенный момент инерции механизма 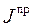 является величиной постоянной, как, например, в зубчатых механизмах, то дифференциальное уравнение движения имеет вид
является величиной постоянной, как, например, в зубчатых механизмах, то дифференциальное уравнение движения имеет вид
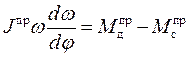 (29)
(29)

|
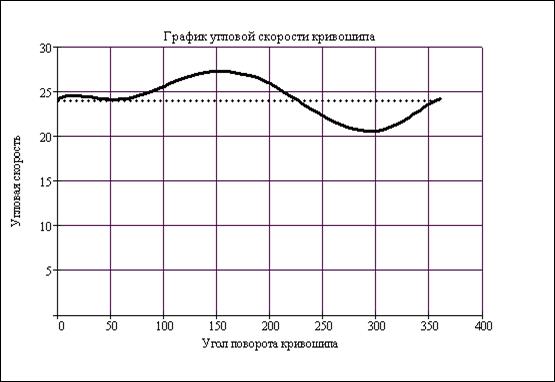
В результате решения дифференциального уравнения (27) на стадии установившегося движения получаем угловую скорость (рис.23) звена приведения (кривошипа 1) в функции угла поворота 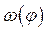 .
.
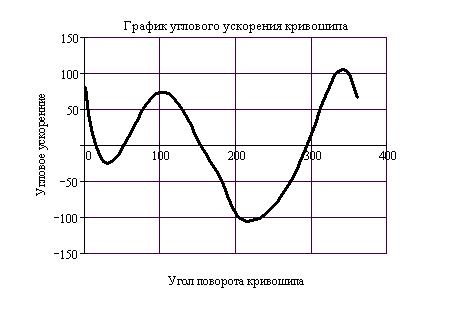
Угловое ускорение кривошипа 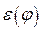 (рис.24) в функции угла поворота определяется по формуле
(рис.24) в функции угла поворота определяется по формуле
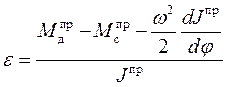 (30)
(30)
|
Для определения времени 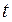 движения звена приведения в зависимости от угла поворота
движения звена приведения в зависимости от угла поворота 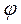 воспользуемся выражением
воспользуемся выражением
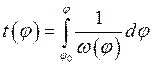 . (31)
. (31)
Приближенное вычисление определенного интеграла Mathcad выполняет с помощью алгоритма численного интегрирования Ромберга.
|
Лабораторная работа 6
Синтез и анализ кулачкового механизма
Синтез кулачкового механизма (рис. 22) выполняем по заданному закону движения толкателя 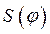 и допускаемым углам давления
и допускаемым углам давления 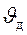 . Основные размеры механизма - минимальный радиус-вектор
. Основные размеры механизма - минимальный радиус-вектор 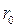 кулачка и эксцентриситет
кулачка и эксцентриситет 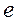 должны быть такими, чтобы во всех положениях механизма углы давления
должны быть такими, чтобы во всех положениях механизма углы давления 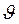 не превышали допускаемого значения
не превышали допускаемого значения
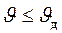 .
.
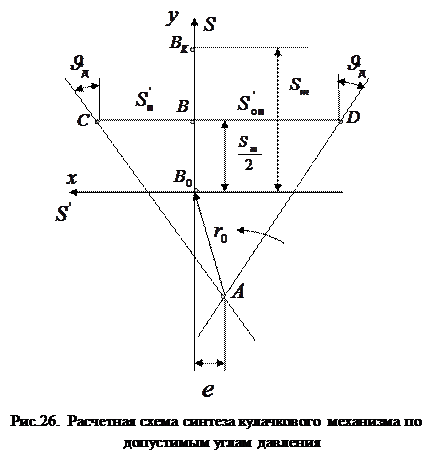
В кулачковых механизмах с поступательно движущимся толкателем максимальное значение угла давления приближенно соответствует положению механизма, при котором аналог скорости 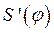 имеет максимальное значение. Для определения основных размеров кулачкового механизма используем упрощенный график перемещения толкателя в функции его аналога скорости
имеет максимальное значение. Для определения основных размеров кулачкового механизма используем упрощенный график перемещения толкателя в функции его аналога скорости 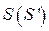 . На этом графике (рис. 23) показаны только максимальные значения аналога скорости на фазах подъема
. На этом графике (рис. 23) показаны только максимальные значения аналога скорости на фазах подъема 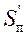 и опускания
и опускания 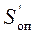 . По оси
. По оси 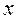 в соответствии с направлением вращения кулачка откладываются максимальные аналоги скорости
в соответствии с направлением вращения кулачка откладываются максимальные аналоги скорости 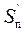 на фазе подъема и
на фазе подъема и 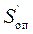 на фазе опускания , а по оси
на фазе опускания , а по оси 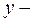 перемещение толкателя. Максимальные значения аналогов скорости возникают в тех положениях механизма, при которых толкатель находится на половине хода
перемещение толкателя. Максимальные значения аналогов скорости возникают в тех положениях механизма, при которых толкатель находится на половине хода 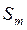 . Через точки
. Через точки 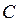 и
и 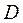 под допустимыми углами давления проведены линии, точка
под допустимыми углами давления проведены линии, точка 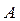 пересечения которых дает положение центра вращения кулачка. При этом получаем механизм с углами давления не превышающими допустимое значение
пересечения которых дает положение центра вращения кулачка. При этом получаем механизм с углами давления не превышающими допустимое значение 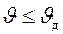 .
.
|
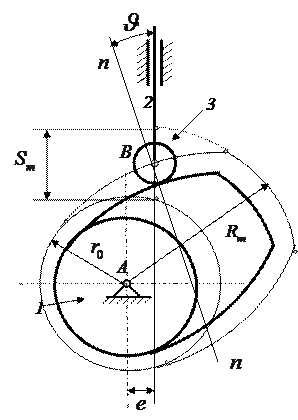 |
Координаты 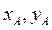 точки
точки 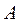 определяются в результате пересечения двух прямых, проходящих через точки
определяются в результате пересечения двух прямых, проходящих через точки 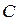 и
и 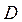 (рис.26). Уравнения прямых
(рис.26). Уравнения прямых
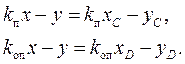 (33)
(33)
Решением системы линейных уравнений являются координаты 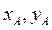 точки
точки 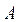 центра вращения кулачка. В этом уравнении
центра вращения кулачка. В этом уравнении
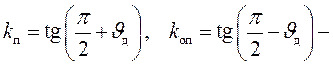 угловые коэффициенты прямых линий
угловые коэффициенты прямых линий 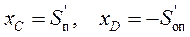 координаты точек
координаты точек 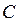 и
и 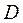
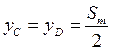 .
.
 |
Минимальный радиус-вектор центрового профиля кулачка и эксцентриситет определяются по формулам
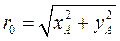 ,
, 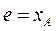 . (34)
. (34)
При решении системы линейных уравнений в системе Mathcad Pro можно использовать функцию 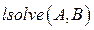 . Порядок использования этой функции изложен в лабораторной работе 1. В работе рассмотрим символьное решение системы линейных уравнений (рис.27).
. Порядок использования этой функции изложен в лабораторной работе 1. В работе рассмотрим символьное решение системы линейных уравнений (рис.27).
Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующие действия:
· напечатать слово 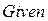 , это слово сообщающее программе Mathcad, что далее следует система уравнений;
, это слово сообщающее программе Mathcad, что далее следует система уравнений;
· напечатать ниже слова 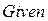 уравнения системы в любом порядке. Знак равенства в уравнениях является знаком логического равенства. Для его ввода используется палитра символов или сочетание клавиш
уравнения системы в любом порядке. Знак равенства в уравнениях является знаком логического равенства. Для его ввода используется палитра символов или сочетание клавиш 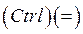 ;
;
· напечатать функцию 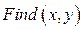 . Аргументами функции являются переменные, относительно которых система решается;
. Аргументами функции являются переменные, относительно которых система решается;
· напечатать символьный знак равенства 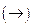 , для этого используется палитра символов или сочетание клавиш
, для этого используется палитра символов или сочетание клавиш  .
.
· щёлкнуть мышью на функции 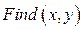 .
.

|
Система Mathcad отображает решение уравнений справа от стрелки в виде вектора результатов. Верхняя формула предназначена для вычисления координаты по оси 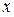 , нижняя по оси
, нижняя по оси 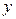 .
.
На рис.28 показан фрагмент программы по расчету профиля кулачка для синусоидального закона движения толкателя с использованием функций пользователя.
В этом фрагменте использованы следующие имена функций для расчета:
· 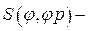 положения толкателя,
положения толкателя,
· 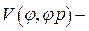 скорости толкателя,
скорости толкателя,
· 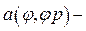 ускорения толкателя,
ускорения толкателя,
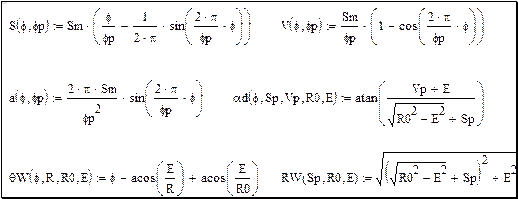
|
· 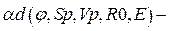 углов давления,
углов давления,
· 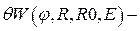 углов профиля кулачка,
углов профиля кулачка,
· 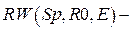 радиус-вектора кулачка.
радиус-вектора кулачка.
В скобках после имени функции указываются параметры, являющиеся входными в функцию.
Далее на рис. 29 показан расчетный блок с именем 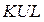 , с помощью которого вычисляются закон движения толкателя и профиль кулачка. В составе расчетного блока
, с помощью которого вычисляются закон движения толкателя и профиль кулачка. В составе расчетного блока 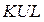 используется оператор цикла
используется оператор цикла 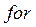 , условный оператор
, условный оператор 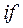 и оператор иного выбора
и оператор иного выбора 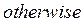 , а также функции пользователя, показанные выше на рис. 28.
, а также функции пользователя, показанные выше на рис. 28.
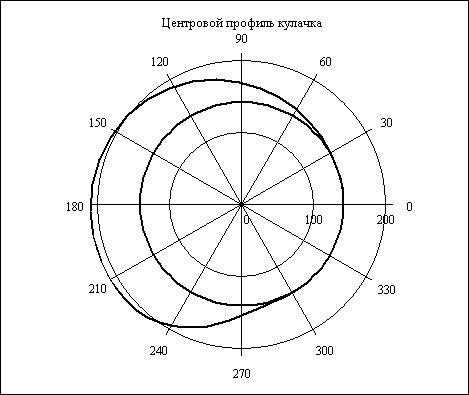
По результатам расчета в полярной системе координат построен центровой профиль кулачка (рис.30). Команда 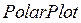 (полярный график) или нажатие комбинации
(полярный график) или нажатие комбинации 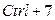 выводит на экран монитора шаблон таких графиков. Этот шаблон
выводит на экран монитора шаблон таких графиков. Этот шаблон
имеет форму окружности и содержит места ввода данных. Слева от шаблона указывается имя радиус-вектора профиля кулачка, а снизу углов профиля.

|
|
Лабораторная работа № 7
Силовой анализ кривошипно-ползунного механизма
Исходными данными для расчета (рис.31) являются: 1) кинематическая схема механизма; 2) массы и моменты инерции звеньев, а также положение центров масс; 3) силы полезного сопротивления; 4) закон движения входного звена-1.
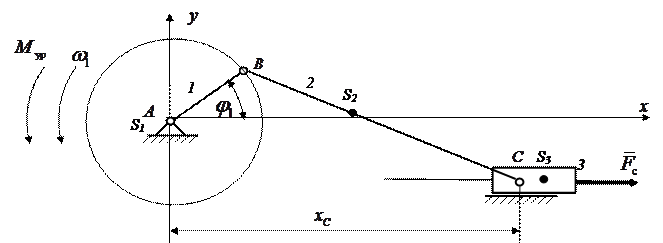 | |||
| |||
На рис.31 показана сила полезного сопротивления 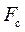 , приложенная к ползуну 3 и уравновешивающий момент
, приложенная к ползуну 3 и уравновешивающий момент 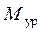 , действующий на кривошип 1. Перед выполнением силового расчета необходимо провести кинематический анализ механизма и определить положение звеньев и центров масс, ускорения центров масс и угловые ускорения звеньев. Используя результаты кинематического анализа, определяем силы инерции в проекциях на координатные оси и моменты сил инерции по формулам
, действующий на кривошип 1. Перед выполнением силового расчета необходимо провести кинематический анализ механизма и определить положение звеньев и центров масс, ускорения центров масс и угловые ускорения звеньев. Используя результаты кинематического анализа, определяем силы инерции в проекциях на координатные оси и моменты сил инерции по формулам
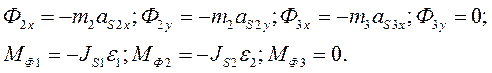 (35)
(35)
где 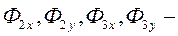 проекции сил инерции звеньев на координатные оси;
проекции сил инерции звеньев на координатные оси;
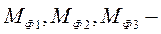 моменты сил инерции звеньев относительно центров масс.
моменты сил инерции звеньев относительно центров масс.
 Выделяем из механизма структурную группу 2-3 и показываем силы, действующие на звенья ( рис. 32)
Выделяем из механизма структурную группу 2-3 и показываем силы, действующие на звенья ( рис. 32)
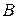
|

Составляем уравнения равновесия сил, действующих на выделенную структурную группу. Таких уравнений для двух звеньев группы будет шесть.
Уравнения сил и моментов сил, действующих на звено 2,
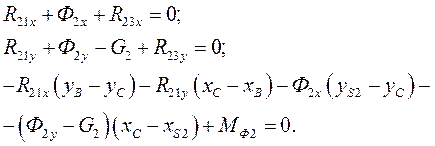 (36)
(36)
Уравнения сил и моментов сил, действующих на звено 3.
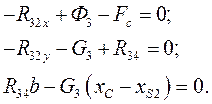 (37)
(37)
Приводим систему шести линейных уравнений к каноническому виду:
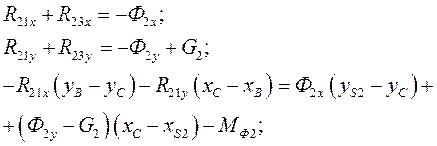
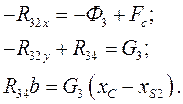 (38)
(38)
Составляем матрицу 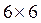 коэффициентов, стоящих в левой части системы линейных уравнений, и матрицу-столбец коэффициентов, стоящих в правой части системы:
коэффициентов, стоящих в левой части системы линейных уравнений, и матрицу-столбец коэффициентов, стоящих в правой части системы:
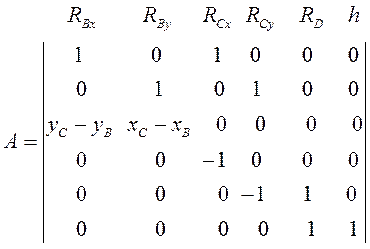
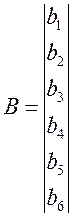 (39)
(39)
где
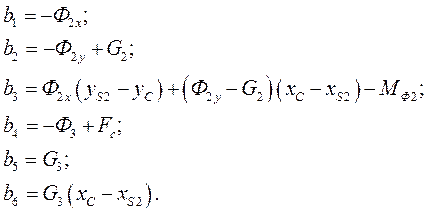
Для решения системы шести линейных уравнений 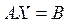 также целесообразно использовать функцию
также целесообразно использовать функцию 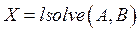 . Результат решения представляем в виде столбцевой матрицы
. Результат решения представляем в виде столбцевой матрицы
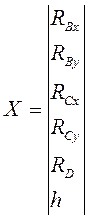 (40)
(40)
Величину реакций определяем по формулам
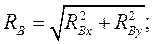
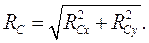 (41)
(41)
Угол, определяющий направление вектора силы в прямоугольной системе
координат вычисляем с помощью функции 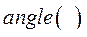
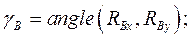
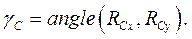 (42)
(42)
Используя полярную систему координат, строим годограф сил, действующих в кинематических парах. На рис. 33 показан годограф сил для кинематической пары 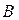 между звеньями 1 и 2. Годограф сил позволяет определить положения механизма, при которых реакции в кинематических парах имеют максимальное значение
между звеньями 1 и 2. Годограф сил позволяет определить положения механизма, при которых реакции в кинематических парах имеют максимальное значение
|
Затем выполняем силовой расчет кривошипа 1. Уравновешивающий момент определяем из уравнения моментов относительно точки 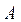 :
:
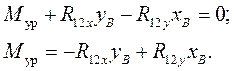 (43)
(43)
Для определения реакции 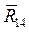 в кинематической паре
в кинематической паре 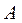 проектируем силы, действующие на звено 1 на координатные оси.
проектируем силы, действующие на звено 1 на координатные оси.
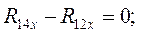
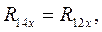 (44)
(44)
Величину реакции и угол 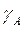 , определяющий направление вектора
, определяющий направление вектора 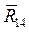 , вычисляем по формулам, аналогичным (41), (42).
, вычисляем по формулам, аналогичным (41), (42).
Лабораторная работа 8
Исследование движения упругого толкателя в кулачковом механизме
Математическая модель кулачкового механизма, составленная в предположении, что его звенья являются абсолютно жесткими, во многих случаях, особенно для быстроходных механизмов, дает результаты, существенно отличающиеся от действительных [2]. Наблюдаются значительные отклонения от идеального ускорения для законов движения с “жесткими” и “мягкими” ударами. Поэтому рассмотрим формулы, учитывающие влияние упругости толкателя на его закон движения. При этом предполагаем, что кулачок является абсолютно твердым телом, а масса толкателя сосредоточена в одной точке. Силы упругости толкателя представляются силами упругости пружины, помещенной между массой 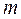 и кулачком ( рис.31). Перемещение
и кулачком ( рис.31). Перемещение 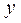 верхнего конца толкателя вследствие его упругости отличается от перемещения
верхнего конца толкателя вследствие его упругости отличается от перемещения 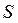 нижнего конца, который движется по профилю кулачка. Движение массы
нижнего конца, который движется по профилю кулачка. Движение массы 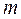 определяется дифференциальным уравнением
определяется дифференциальным уравнением
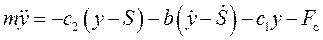 , (45)
, (45)
где 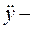 ускорение массы
ускорение массы 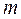 с учетом упругости толкателя;
с учетом упругости толкателя; 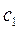 и
и 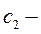 коэффициенты жесткости соответственно замыкающей пружины и толкателя;
коэффициенты жесткости соответственно замыкающей пружины и толкателя; 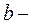 коэффициент
коэффициент
 |
пропорциональности силы сопротивления, возникающей при деформации упругого толкателя; 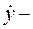 скорость массы
скорость массы 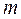 с учетом упругости толкателя;
с учетом упругости толкателя; 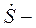 скорость толкателя, определяемая идеальным законом движения;
скорость толкателя, определяемая идеальным законом движения; 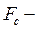 сила сопротивления, включающая силу трения и силу предварительного натяжения пружины.
сила сопротивления, включающая силу трения и силу предварительного натяжения пружины.
Введем в рассмотрение деформацию 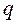 упругого толкателя. При этом
упругого толкателя. При этом
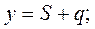
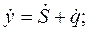
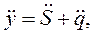 (46)
(46)
где 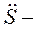 ускорение толкателя (идеальное);
ускорение толкателя (идеальное); 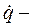 скорость колебательного движения;
скорость колебательного движения; 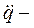 ускорение колебательного движения.
ускорение колебательного движения.
После подстановки (46) в выражение (45) получим дифференциальное уравнение колебаний упругого толкателя
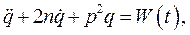 (47)
(47)
где 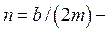 коэффициент демпфирования;
коэффициент демпфирования; 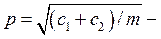 собственная частота колебаний толкателя;
собственная частота колебаний толкателя; 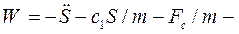 правая часть дифференциального уравнения. Большое влияние на колебательный процесс оказывает закон изменения ускорения
правая часть дифференциального уравнения. Большое влияние на колебательный процесс оказывает закон изменения ускорения 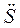 , поэтому в дальнейшем проанализируем влияние идеального закона движения на колебание толкателя. При этом допущении дифференциальное уравнение (47) имеет вид
, поэтому в дальнейшем проанализируем влияние идеального закона движения на колебание толкателя. При этом допущении дифференциальное уравнение (47) имеет вид
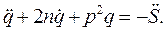 (48)
(48)
Решение этого дифференциального уравнения второго порядка с постоянными коэффициентами зависит от вида его правой части, и для каждого закона движения толкателя необходимо проводить символьные преобразования с целью получения расчетных формул. Как известно, программная система Mathcad PRO [1] имеет набор функций, выполняющих решение дифференциальных уравнений численными методами, что позволяет получить решение дифференциального уравнения, не выполняя длительных и трудоемких символьных преобразований. На рис. 33 показан фрагмент программы для решения дифференциального уравнения (48) с помощью функции rkadapt ( y , x 1, x 2, acc , n , D , k , s ). Эта функция возвращает матрицу, содержащую таблицу значений решения задачи Коши на интервале от х1... х2 для системы обыкновенных дифференциальных уравнений, вычисленную методом Рунге-Кутта с переменным шагом интегрирования и начальными условиями описанными в векторе y , (правые части системы записаны в векторе D , n – число шагов, k– максимальное число промежуточных точек решения, и s– минимально допустимый интервал между точками, асс– погрешность вычисления). Эта функция благодаря автоматическому изменению шага интегрирования даёт более точный результат. Функция rkadapt наиболее привлекательна для решения дифференциальных уравнений, имеющих относительно медленно изменяющиеся решения наряду с быстрыми их изменениями.

|
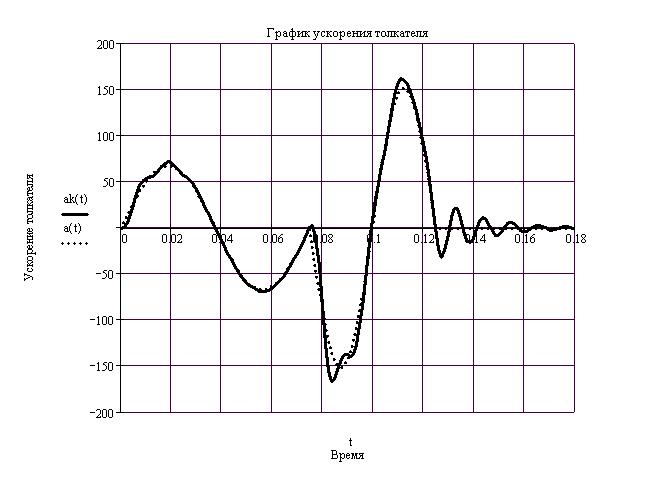
Результат решения дифференциального уравнения (48) для закона движения толкателя с постоянным ускорением в виде графика показан на рис. 34, для движения по синусоидальному закону на рис. 35. Пунктирная линия соответствует идеальному закону движения, основная линия ускорению толкателя с учетом его упругости. Как видно из графиков закон движения с постоянным ускорением имеет разрывы, является законом “с мягкими ударами”, которые оказывают существенное влияние на колебание толкателя. Наиболее резкие “скачки” ускорения наблюдаются в местах разрыва идеальной функции 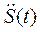 . При плавном, синусоидальном законе движения не имеющем разрывов, амплитуда колебаний ускорения толкателя значительно меньше, чем при законе с постоянным ускорением. Расчеты
. При плавном, синусоидальном законе движения не имеющем разрывов, амплитуда колебаний ускорения толкателя значительно меньше, чем при законе с постоянным ускорением. Расчеты

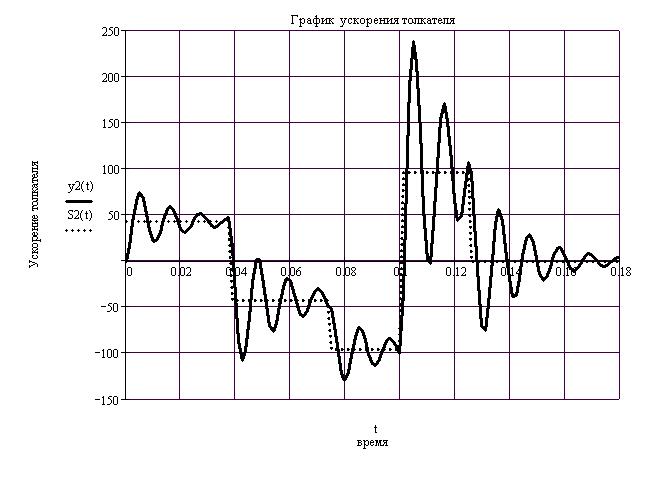
ускорения были выполнены при следующих исходных данных: ход толкателя 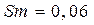 м, масса толкателя
м, масса толкателя 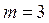 кг, коэффициент жесткости
кг, коэффициент жесткости 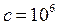 Н/м, коэффициент демпфирования
Н/м, коэффициент демпфирования 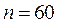 Н/с*мм угловая скорость кулачка
Н/с*мм угловая скорость кулачка 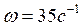 , фазовый угол подъема
, фазовый угол подъема 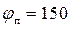 град, опускания
град, опускания 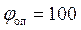 град. Частота собственных колебаний
град. Частота собственных колебаний 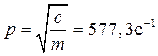 , частота кинематического возмущения на фазе подъема
, частота кинематического возмущения на фазе подъема
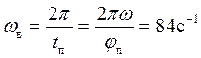 ,
,
на фазе опускания 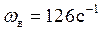 .
.
Максимальный коэффициент динамичности при законе движения толкателя с постоянным ускорением составляет 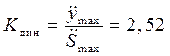 ,
,

|
|
при синусоидальном законе 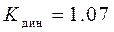 .
.
Коэффициент максимального ускорения при законе движения толкателя с постоянным ускорением составляет 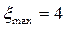 , при синусоидальном законе
, при синусоидальном законе 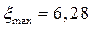 . Однако расчет, выполненный с учетом упругости толкателя показывает, что при плавном синусоидальном законе максимальная величина ускорения
. Однако расчет, выполненный с учетом упругости толкателя показывает, что при плавном синусоидальном законе максимальная величина ускорения 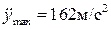 меньше, чем при законе движения с постоянным ускорением
меньше, чем при законе движения с постоянным ускорением 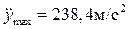 . Следовательно, при синусоидальном законе ниже инерционные нагрузки, действующие на профиль кулачка, и при прочих равных условиях выше его долговечность.
. Следовательно, при синусоидальном законе ниже инерционные нагрузки, действующие на профиль кулачка, и при прочих равных условиях выше его долговечность.
Список литературы
1. В. Дьяконов. Mathcad 2001. Учебный курс. – СПб.: Питер, 2001.
2. Механика машин:/ под ред. Г.А. Смирнова – М.: Высшая школа, 1996.








