Забайкальский институт железнодорожного транспорта
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Иркутский государственный университет путей сообщения»
(ФГБОУ ВО ИрГУПС)
Забайкальский институт железнодорожного транспорта
- филиал Федерального государственного бюджетного образовательного учреждения высшего образования
«Иркутский государственный университет путей сообщения»
(ЗабИЖТ ИрГУПС)
Факультет очного обучения
Кафедра «Электроснабжение»
Лабораторные работы
ЛР. 510740.23.05.03.ПЗ
| Выполнил студент гр. ПСЖ 3-19-1 Привалов Д. В. «___»________2020 г.__________ | Проверил Ассистент Маниковский А.С. «____»________2020 г.__________ |
Чита 2020
ЛАБОРАТОРНАЯ РАБОТА № 2. Экспериментальная проверка принципа наложения и теоремы об эквивалентном генераторе
Цель работы: экспериментальная проверка теоремы об эквивалентном генераторе на примере сложной электрической цепи постоянного тока.
Теоретическое обоснование
Метод наложения. Для линейных электрических цепей справедлив принцип наложения, согласно которому ток в какой-либо ветви может быть определен как алгебраическая сумма частичных токов, создаваемых отдельными источниками энергии. На этом принципе основывается расчет электрической цепи методом наложения, согласно которому с использованием законов Кирхгофа рассчитываются токи от действия каждого источника в отдельности. На месте остальных источников при этом остается только их внутреннее сопротивление. Выполняя наложение результатов расчета частичных токов с учетом их направлений, получим значения действительных токов в ветвях.
Метод эквивалентного генератора. Данный метод основан на теореме об эквивалентном генераторе: любой активный двухполюсник в расчетном отношении может быть заменен эквивалентным генератором, ЭДС которого равно напряжению на разомкнутых зажимах двухполюсниках (при холостом ходе), а внутреннее сопротивление – входному сопротивлению соответствующего пассивного двухполюсника.
Пассивный двухполюсник получается из активного, если исключить источники энергии, оставив в схеме их внутреннее сопротивление. Это метод применяется, как правило, в том случае, если требуется определить ток в какой-либо одной ветви сложной схемы. Например, в схеме (рис. 15) требуется определить ток в ветви аb.
Относительно зажимов аb (рис. 15, а) выделенная часть схемы является активным двухполюсником (рис. 15, б) и может быть заменена эквивалентным генератором (рис. 15, в).
В результате сложная схема заменяется неразветвленной цепью, в которой ток определяется как
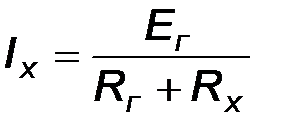
| (15) |
ЭДС и внутреннее сопротивление генератора могут быть определены расчетным или опытным путем. В последнем случае напряжение холостого хода активного двухполюсника равно ЭДС эквивалентного генератора (рис. 16, а), а внутреннее сопротивление определяется из опыта короткого замыкания (рис. 16, б).
а)
б) в)
Рис. 15. Исследуемая схема цепи (а), представленная активным двухполюсником (б) и эквивалентным генератором (в).
Рис. 16. Опыт холостого хода и короткого замыкания: а) опыт холостого хода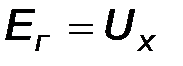 
; б) опыт короткого замыкания 
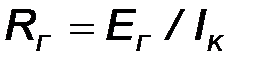, где IК – ток эквивалентного генератора при коротком замыкании зажимов аb.
Экспериментальная часть
В работе исследуется сложная линейная электрическая цепь с двумя источниками энергии, представленная на рис. 17.
а)
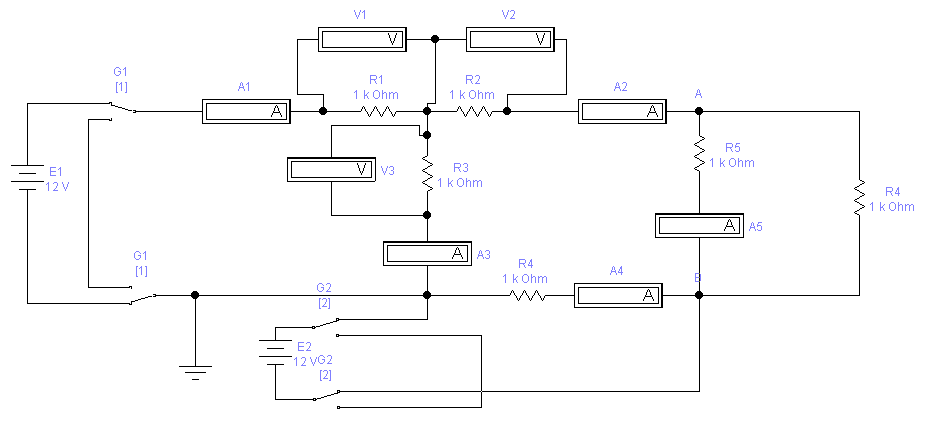
б)
а) – схема в обычном формате; б) – в Elektronic WorkBench 5.12
Рис. 17. Экспериментальная схема
Напряжение источников питания постоянного тока подведено к переключателям П1 и П2. Резисторы и все необходимые приборы установлены на стенде. Для измерения напряжений на всех участках цепи используется один вольтметр со щупами.
Расчёты:
Еэкв=Ux=IR5=E*R5/R1+R2+R3+R4 = 36*2,3/3+2,1+2,1+1=10,1 В
Rэкв=(R1+R2+R3+R4)*R5/R1+R2+R3+R4+R5=(3+2,1+2,1+1)*2,3/3+2,1+2,1+1+2,3 =1,8м
Rab=10м
Ix=Eэкв/(Rab+ Rэкв)=10,1/(1+1,8)=3,6 А
Iк=Еэкв/ Rэкв=10,1/1,8=5,6 А
Опыт №1 (G1 - 1, G2 - 1):
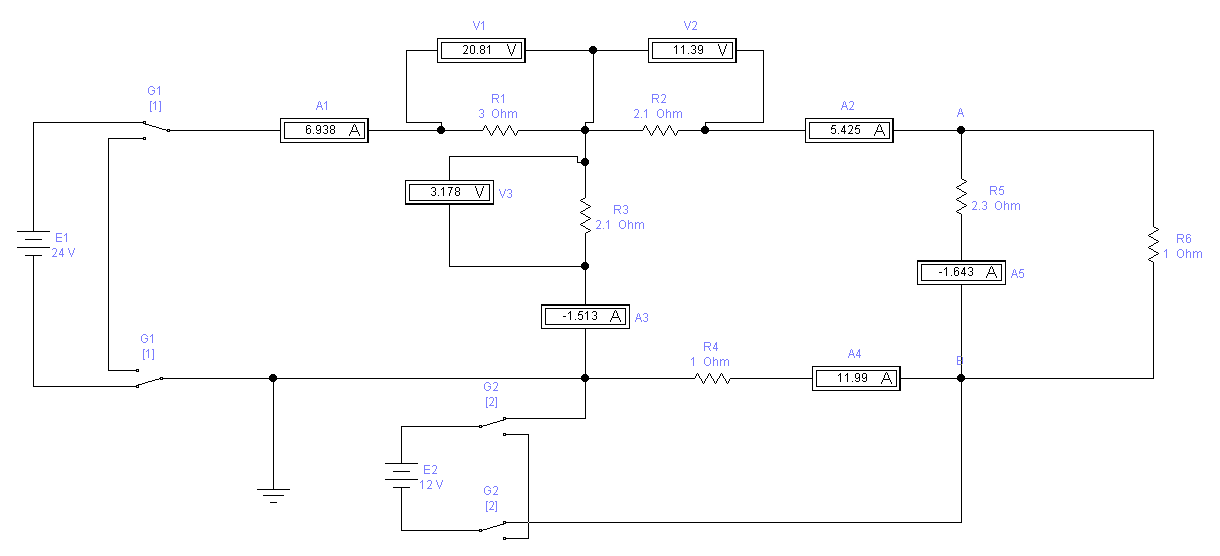
R=U/I
U=R*I
I=U/R
R1=20,81/6,938=3 Ом
R2=11,39/5,425=2,1 Ом
R3=3,178/-1,513=|-2,1| Ом=2,1 Ом
U4=1*11,99=11,99 B
R4=11,99/11,99=1 Ом
U5=2,3*(-1,643)=-3,7789 В
R5=-3,7789/-1,643=2,3 Ом
U6=U5=-3,7789 В
R6=R4=1 Ом
I6=(-3,7789)/1=-3,7789 А
Опыт №2 (G1 - 1, G2 - 2):
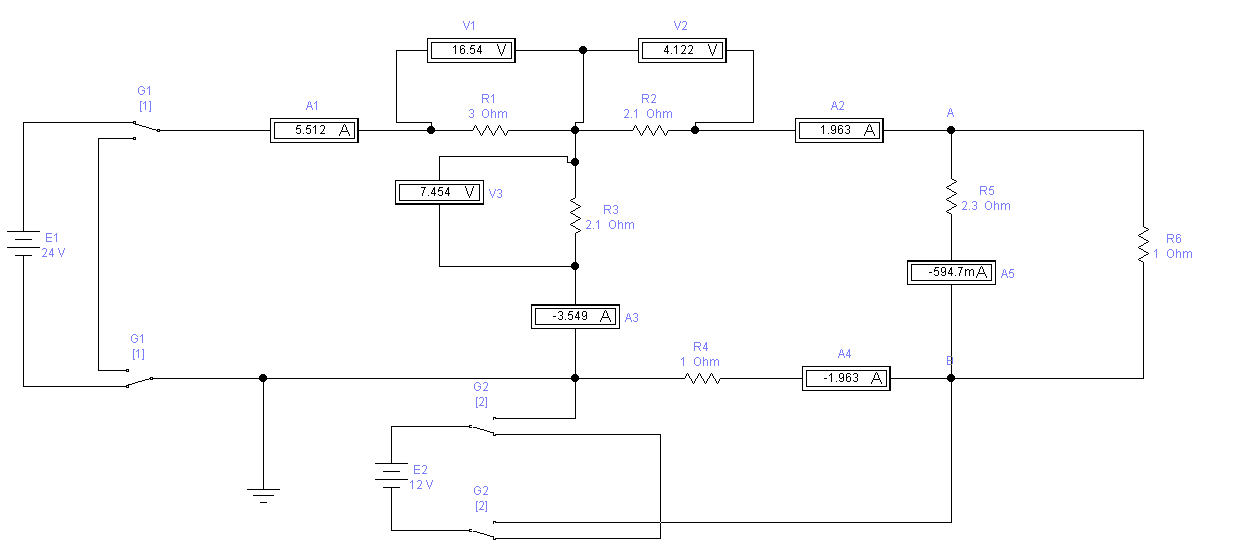
R=U/I
U=R*I
I=U/R
R1=16,54/5,512=3 Ом
R2=4,122/1,963=2,1 Ом
R3=7,454/(-3,549)=|-2,1| Ом=2,1 Ом
U4=1*(-1,963)=-1,963 B
R4=-1,963/-1,963=1 Ом
U5=2,3*(-0,5947)=-1,3678 В
R5=-1,3678/-0,5947=2,3 Ом
U6=U5=-1,3678 В
R6=R4=1 Ом
I6=(-1,3678)/1=-1,3678 А
Опыт №3 (G1 - 2, G2 - 1):
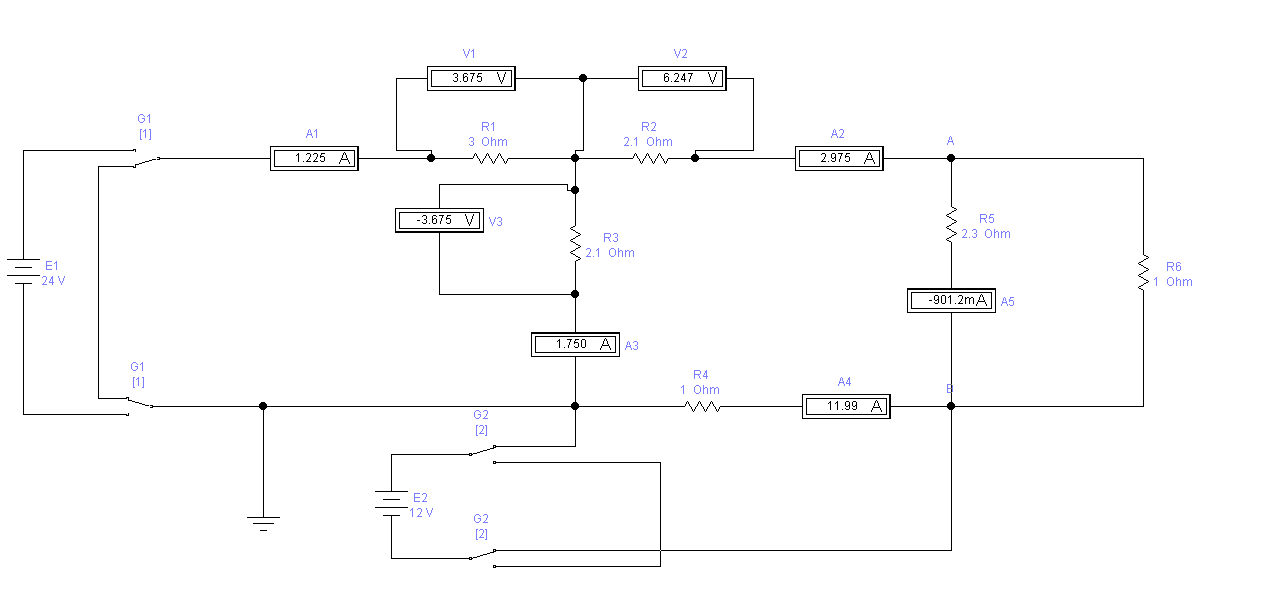
R=U/I
U=R*I
I=U/R
R1=3,675/1,225=3 Ом
R2=6,247/2,975=2,1 Ом
R3=-3,675/1,750=|-2,1| Ом=2,1 Ом
U4=1*11,99=11,99 B
R4=11,99/11,99=1 Ом
U5=2,3*(-0,9012)=-2,0727 В
R5=-2,0727/-0,9012=2,3 Ом
U6=U5=-2,0727 В
R6=R4=1 Ом
I6=(-2,0727)/1=-2,0727 А
Таблица 1 - Результаты лабораторной работы № 2
| Опыт | Измерено | Вычислено | ||||||||||||||||
| напряжение, В | токи, мА | сопротивление, Ом | ||||||||||||||||
| Ur1 | Ur2 | Ur3 | Ur4 | Ur5 | Ur6 | I1 | I2 | I3 | I4 | I5 | I6 | R1 | R2 | R3 | R4 | R5 | R6 | |
| G1 - 1 G2 - 1 | 220,81 | 111,39 | 33,178 | 111,99 | --3,7789 | --3,7789 | 66938 | 55425 | -1513 | 11199 | -1643 | -3778,9 | 33 | 22,1 | 22,1 | 11 | 22,3 | 11 |
| G1 - 1 G2 - 2 | 116,54 | 44,122 | 77,454 | --1,963 | --1,3678 | --1,3678 | 55512 | 11936 | --3549 | --1963 | --549,7 | --1367,8 | 33 | 22,1 | 22,1 | 11 | 32,3 | 11 |
| G1 - 2 G2 - 1 | 33,675 | 66,247 | --3,675 | 111,99 | --2,0727 | --2,0727 | 11225 | 22975 | 11750 | --0901,2 | --2072,7 | 33 | 22,1 | 22,1 | 11 | 22,3 | 11 | |
Таблица 2 - Результаты лабораторной работы № 2
| Метод | Er, B | Ik, A | Rr, Ом | Iх, А |
| Опыт | 10,1 | 5,6 | 1,8 | 3,6 |
| Расчет | 10,1 | 5,6 | 1,8 | 3,6 |
Вывод
На основе схем и выполненных методов наложения и метода об эквивалентном генераторе были определены конкретные значения в составе 3-х опытов. Также проведено сопротивление на каждом участке цепи, далее для нахождения эквивалентной ЭДС, нужно было рассмотреть режим холостого хода генератора, то есть отсоединяя исследуемую ветвь ab избавить генератор от нагрузки. В итоге, чтобы найти эквивалентное сопротивление убираем во внешней цепи источник ЭДС и находим сопротивление цепи.