20.2. Известны длины сторон a, b, c треугольника. Вычислите все высоты этого треугольника.
21.1. Поменять местами значения целых переменных a и b, не используя дополнительные переменные.
21.2. Найдите точку, лежащую на отрезке, соединяющем две данные точки, но находящуюся к первой из них в два раза ближе, чем ко второй. Напишите программу, которая вводит координаты первой точки (x1,y1), координаты второй точки (x2,y2) и выводит координаты искомой точки (x3,y3),.
22.1. Пусть k - целое число от 1 до 365. Присвоить целой переменной n значение 1, 2, 3, 4, 5, 6 или 7 в зависимости от того, на который день недели (понедельник, вторник,...,субботу или воскресенье) приходится k-й день невисокосного года, в котором 1 января – понедельник.
22.2. Задано уравнение прямой Ax+By+C=0 и координаты точки (x,y). Найти расстояние от данной точки до заданной прямой.
Указание. Если у уравнения прямой Ax+By+C=0 оказывается, что A2+B2=1, то это уравнение называется нормальным, и оно обладает важным свойством: при подстановке в это уравнение координат любой точки плоскости левая часть оказывается равной расстоянию от этой точки до данной прямой. Причем, для точек одной полуплоскости это расстояние получается положительным, а для точек другой полуплоскости – отрицательным.
И так, чтобы узнать расстояние от точки до прямой, надо координаты точки подставить в нормальное уравнение прямой. Чтобы получить нормальное уравнение прямой из произвольного имеющегося, надо разделить его на 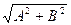 .
.
23.1. Зарплата сотрудника частной фирмы составляет r рублей в месяц. Сколько денег он получит за полгода после вычета налогов в размере t% ежемесячно и s% за полгода?
23.2. Заданы уравнения двух пересекающихся прямых на плоскости: y=k1x+b1 и y=k2x+b2. Найти (в градусах и минутах) угол между ними, используя формулу
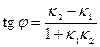 .
.
24.1. Найти сумму членов арифметической прогрессии a, a+d,..., a+(n-1)d по данным значениям a, d, n.
24.2. Найдите точку, лежащую на отрезке, соединяющем две данные точки и расположенной от них на расстояниях, относящихся как a к b. Напишите программу, которая вводит a, b, координаты первой и второй точек и выводит координаты искомой точки.
25.1. Найти координаты вершины параболы y=ax2+bx+c.








