Исследование типовых динамических звеньев в системах автоматического управления

Дата: 2025-05-01; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

ЛАБОРАТОРНАЯ РАБОТА №1

Исследование типовых динамических звеньев
в системах автоматического управления

Цель работы: исследование переходных, амплитудно-фазовых, амплитудных частотных и фазовых частотных характеристик линейных звеньев систем автоматического управления (САУ). Продолжительность работы 4 часа.

1.Теоретическая часть

1.1. Общие положения

При создании системы управления технологическим процессом или промышленным объектом необходимо иметь математическое описание объекта управления, управляющего устройства и других элементов, входящих в систему, которые в дальнейшем будем называть звеньями САУ. Математическое описание или математическая модель звена представляют собой совокупность дифференциальных и алгебраических уравнений, которыми связаны выходные и входные сигналы звена. Алгебраические уравнения описывают установившиеся состояния, т.е. такие состояния, когда все производные входных и выходных сигналов равны нулю. Эти уравнения называются уравнениями статики.

Дифференциальные уравнения характеризуют поведение системы во времени при изменении входных воздействий и называются уравнениями динамики.

Для получения динамических характеристик применяют аналитические и экспериментальные методы. Аналитические методы основаны на законах физики, химии, электротехники и др. Часто оказывается эффективным сочетание аналитических и экспериментальных методов. При этом аналитическим путём находят структуру уравнений связи, а числовые значения коэффициентов уравнений определяют экспериментально.

Все экспериментальные методы базируются на предположении о сосредоточенности параметров звена (системы), стационарности во времени его динамических свойств и линейности их при малых изменениях входных воздействий.

Совокупность рассмотренных допущений позволяет описать динамические свойства отдельного звена или системы управления математическими выражениями следующего вида:

1) дифференциальным уравнением:

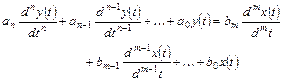(1)

где 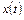- входное воздействие; 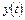- выходной сигнал (управляемая переменная); 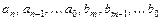- постоянные коэффициенты, определяемые физическими параметрами звена (системы). Для физически реализуемых систем ;

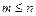2) передаточной функцией:

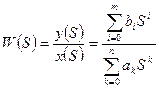, (2)

где 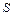- оператор Лапласа; 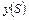и 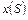- изображения по Лапласу соответственно 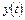и 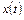при нулевых начальных условиях;

3) комплексной передаточной функцией 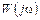, или амплитудно-фазовой характеристикой (АФХ):

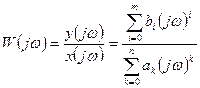, (3)

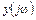где и 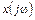- преобразования Фурье соответственно сигналов 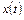и .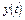

Между перечисленными динамическими характеристиками линейного звена (системы) существует однозначная связь.

Выделяют типовые динамические звенья, из которых можно формировать линейные объекты и системы любой сложности. Динамическое звено описывается дифференциальным уравнением, представляющим частный случай уравнения (1). Этот частный случай предполагает порядок производной в левой части уравнения (2) не выше второго, а в правой его части не выше первого.

1.2. Переходная характеристика звена

Переходной характеристикой 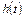называется реакция звена (системы) на ступенчатое единичное воздействие 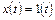при нулевых начальных условиях.

Ступенчатая единичная функция представляет собой мгновенное изменение величины воздействия на единицу (рис. 1.)

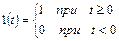. (4)

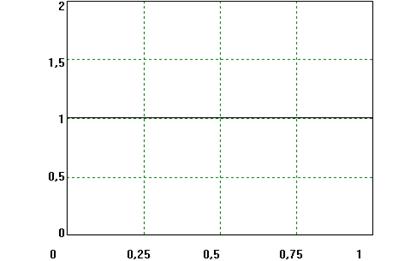
Рис. 1. Ступенчатый единичный сигнал

С помощью единичного скачка может быть получена достаточно надёжная оценка статического коэффициента передачи ( 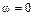) и низкочастотной части динамической характеристики исследуемого звена. Рассматриваемый метод определения динамических характеристик наиболее эффективен для систем первого и второго порядков, реже для апериодических систем высоких порядков.

При известной передаточной функции звена 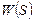переходная характеристика 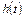определяется аналитически с использованием обратного преобразования Лапласа. Она является решением дифференциального уравнения (1) при входном воздействии в виде (4).

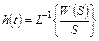, (5)

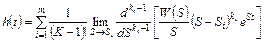, (6)

где 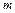- число полюсов функции 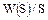, 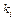- кратность 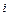-го полюса.

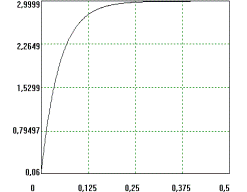
В табл.1 приведены наиболее распространённые переходные характеристики звеньев САУ и их передаточные функции.

1.3.Частотные динамические характеристики

Получить математическую модель звена (системы) в виде произведения передаточных функций типовых звеньев можно по экспериментальным частотным характеристикам.

Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Частотные характеристики имеют простую физическую интерпретацию. Пусть на вход линейного звена подано гармоническое воздействие определенной частоты :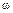

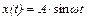. (7)

После окончания переходного процесса выходная величина будет изменяться также по гармоническому закону 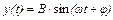с той же частотой 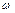, но с отличающейся амплитудой 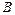и фазовым сдвигом 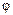(рис. 3.). Изменяя частоту 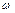в определенном диапазоне, определим зависимость отношения амплитуд выходного и входного сигналов от частоты, которая называется амплитудной частотной характеристикой. Обозначим её : .

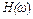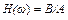x( t)= A∙ sin( ωt) y( t)= B∙ sin( ωt+ φ)

x(jω) y(jω)

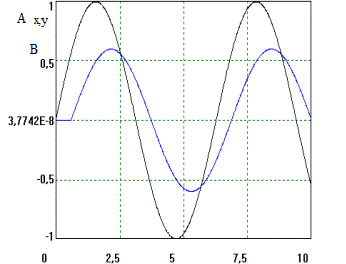
Рис. 2. К определению частотных характеристик

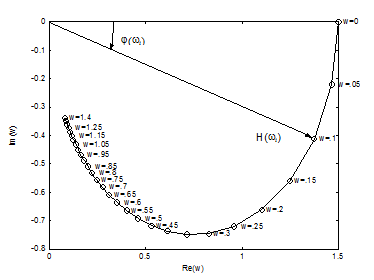
Рис. 3. Амплитудно-фазовая характеристика

Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой 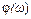. Амплитудная частотная характеристика показывает, как звено пропускает сигналы различной частоты. Оценку усиления (ослабления) производят по отношению между амплитудам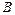и и 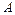. Фазовая частотная характеристика показывает, какое отставание или опережение выходного сигнала по фазе создает звено при различных частотах.

Комплексная передаточная функция, или амплитудно-фазовая характеристика (АФХ), звена 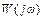представляет собой функцию комплексного переменного 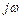. Геометрически она представляет собой траекторию конца вектора на комплексной плоскости в координатах 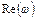и 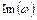, имеющего модуль 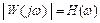и фазу 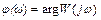при изменении частоты в диапазоне .

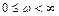Промышленные объекты управления САУ в большинстве своем достаточно инерционные и в динамическом отношении представляют собой фильтры низких частот с небольшой полосой пропускания. Поэтому экспериментальная АФХ для них будет представлять собой небольшой отрезок кривой, соответствующий низким частотам (рис.4). Для определения типа динамического звена и его параметров наибольшее распространение получили логарифмические частотные характеристики (ЛЧХ). ЛЧХ состоят из логарифмических амплитудно-частотной (ЛАЧХ) и фазово-частотной (ЛФЧХ) характеристик.

ЛАЧХ называется график зависимости 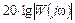от 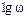, ЛФЧХ называется график зависимости 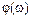от .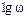

При аппроксимации ЛЧХ передаточной функцией можно строить только ЛАЧХ, т.к. для минимально-фазовых систем она однозначно определяет динамические характеристики. Минимально-фазовыми называются системы, которые описываются передаточными функциями, не имеющими положительных корней ни в полиноме числителя, ни в полиноме знаменателя. Для построения ЛАЧХ на вход исследуемого звена (системы) подается гармонический сигнал, частота 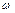которого изменяется в определенном диапазоне, и производится измерение амплитуды выходного сигнала.

Усиление 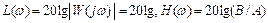, измеряемое в децибелах, откладывается в линейном масштабе по оси ординат графика ЛАЧХ.

По оси абсцисс откладывается угловая частота 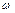в логарифмическом масштабе или ее десятичный логарифм. Отрезок логарифмической шкалы, соответствующий увеличению частоты 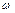в десять раз, называется одной декадой (рис.4).

Таблица 1

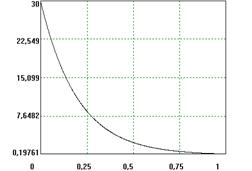
Временные характеристики

№	Передаточная функция звена	Переходная характеристика (кривая разгона) звена
1	2	3
1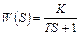
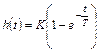
2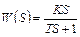

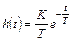
Продолжение табл. 1

1	2	3
3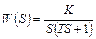
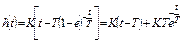
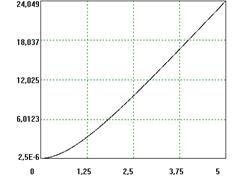
4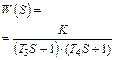

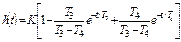
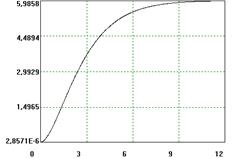
Окончание табл. 1.

1	2	3
5		, ,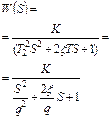

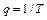
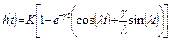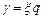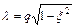
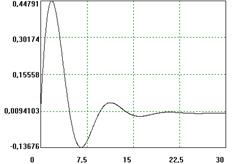
2. Задание для лабораторной работы

Лабораторная работа 1:

1. Смоделировать переходные характеристики динамических звеньев, приведенных в табл. 1 (5 шт.). Варианты параметров звеньев получить у преподавателя (ЛР 1). Моделирование провести в программе tay 2

Лабораторная работа 2:

2. Смоделировать АФХ исследуемых звеньев, приведенных в табл. 1. (ω = рад/ед.времени) (ЛР 2)

3. Смоделировать амплитудные и фазовые частотные характеристики исследуемых звеньев. (ЛР 2)

3. Содержание отчёта

1. Передаточные функции исследуемых звеньев.

2. Уравнения, описывающие переходные характеристики исследуемых звеньев.

3. Переходные характеристики исследуемых звеньев.

4. Амплитудно-фазовые характеристики исследуемых звеньев.

5. Математические выражения для амплитудных и фазовых частотных характеристик исследуемых звеньев.

6. Амплитудные и фазовые частотные характеристики исследуемых звеньев.

4. Контрольные вопросы:

1. Какое звено называют типовым динамическим звеном?

2. Что представляет собой переходная характеристика?

3. Как математически сформулировать определение АФХ?

4. Какой геометрический смысл имеет АФХ?

5. Какой физический смысл имеет АЧХ?

6. Какой физический смысл имеет ФЧХ?