Лаборатория моделирования динамических систем
СПБГМТУ
Кафедра судовой автоматики и измерений
Лаборатория моделирования динамических систем
Лабораторная работа №4
Исследование системы автоматического регулирования
(машина-двигатель, управляемая регулятором Ф. Дженкина).
Условие устойчивости Д. К. Максвелла.
по дисциплине
«Теория автоматического управления»
Выполнил:
Студент группы №5340
Беляков Михаил Юрьевич
Проверил:
Ассистент
Фёдорова Ольга Игоревна
Санкт – Петербург
2018 год
Оглавление
Цель работы ...........................................................3
Дифференциальное уравнение.............................3
Решение дифференциального уравнения............3
Структурная схема .................................................4
Графики...................................................................5
График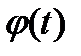 
............................................................6
График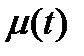 
............................................................6
График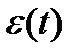 
............................................................7
Фазовый портрет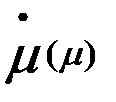 
……………………………………………………………....7
Фазовый портрет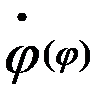 
……………………………………………………………....8
После изменения параметров регулятора
Изменяем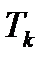 
Графики 2……………………………………………………………..9
График 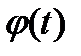...........................................................10 График 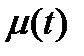............................................................10
График 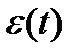…………………………………………………………11
Фазовый портрет 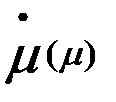……………………………………………………………..11
Фазовый портрет 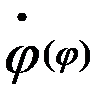……………………………………………………………..12
ЦЕЛЬ РАБОТЫ
Получение практических навыков в исследовании устойчивости состояний равновесия простейших астатических систем автоматического регулирования.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
Математической моделью машины – двигателя, управляемой астатическим регулятором является система дифференциальных уравнений следующего вида:
Система автоматического регулирования
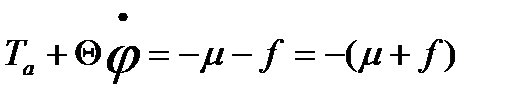Машина – двигатель
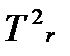μ̈+ 
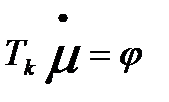Регулятор Ф. Дженкина
Где:
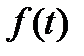- внешнее возмущающее воздействие
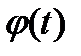- регулируемая величина (входной сигнал регулятора)
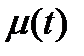- регулирующее воздействие (выходной сигнал регулятора).
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ:
Уравнение относительно переменной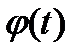 
:
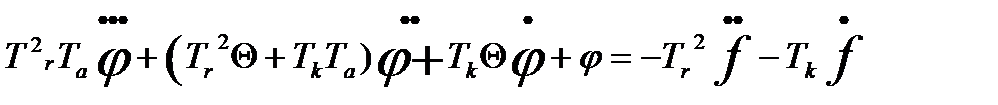
Уравнение относительно переменной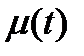 
:
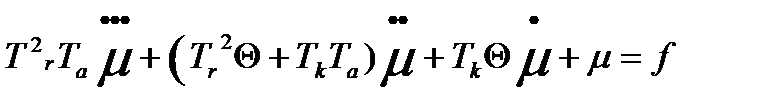
СТРУКТУРНАЯ СХЕМА
ГРАФИКИ
Снимаем наши графики при данных:
Tr2=2
Tа=2
T k =1
=5
Графики 1
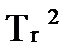
| 2 |
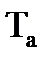
| 2 |
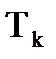
| 1 |
| 5 |
| -1<f<1 | 1 |
| Время выполнения. | 100 |
| Шаг | 0,01 |
| Фазовый портрет. Время наблюдения | 90000 |
График 1.1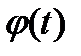
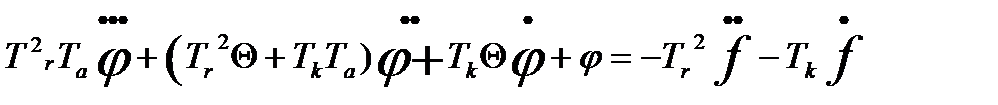
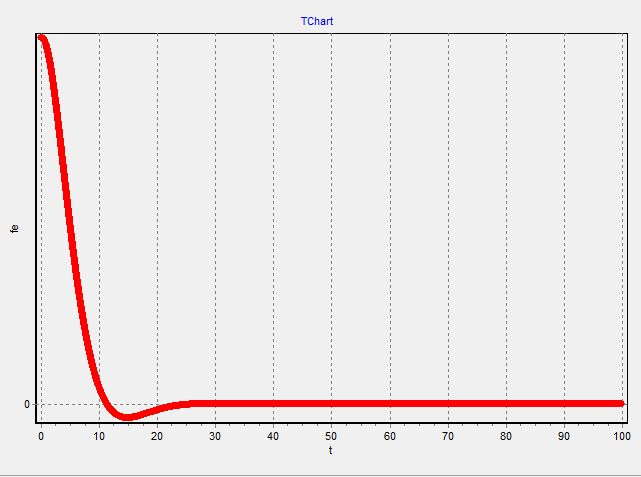
График 1.2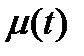
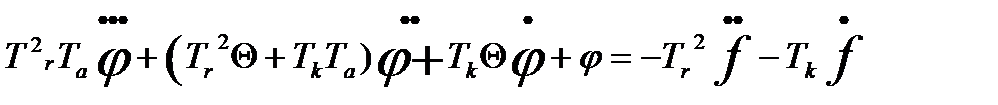
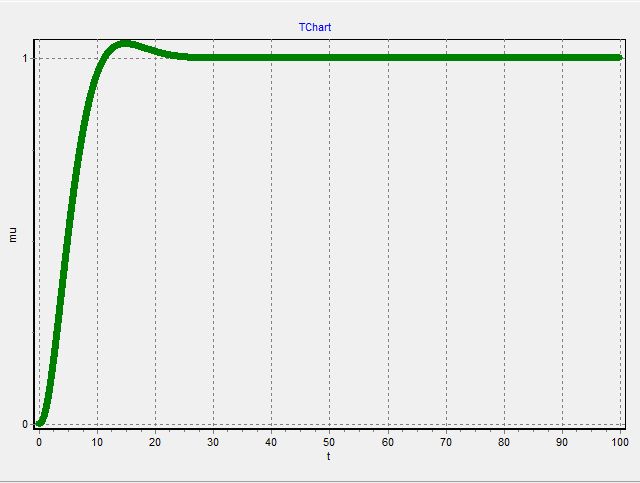
График 1.3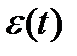 
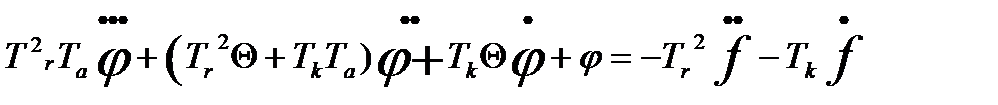
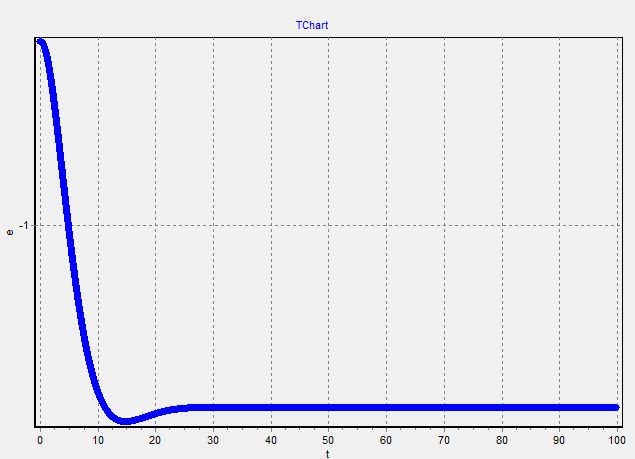
График 2.1
1.4 Фазовый портрет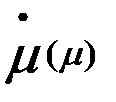
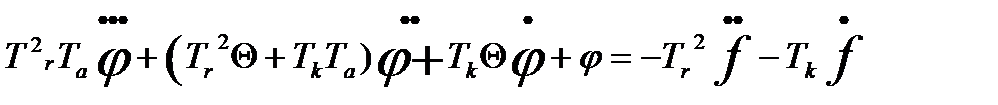
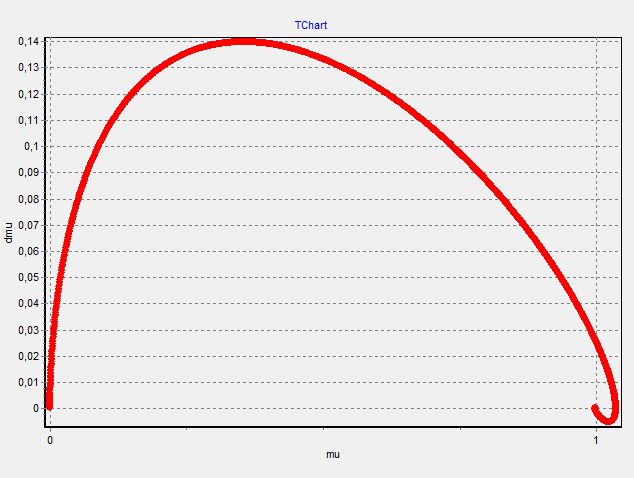
График 2.2
1.5 Фазовый портрет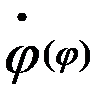
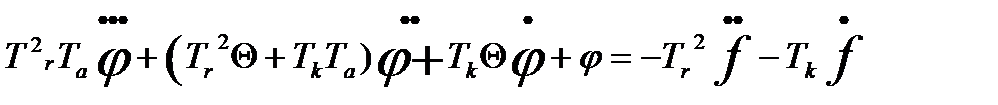
3. Состояние равновесия данной системы будет устойчивым, если удовлетворяется условие:
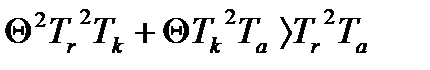- Условие Максвелла.
Подставив наши данные в уравнение, получим:
25·2·1+5·1·2
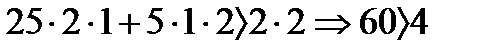
Так как выполняется условие Максвелла, в нашем случае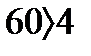 
, то система устойчива.
Система устойчива потому, что все графики заканчиваются установившемся режимом.
Кроме того, все фазовые портреты закручиваются по часовой стрелке, что также говорит об устойчивости системы.
4. Используя условие Максвелла изменяем параметры регулятора переведя систему в другое качественное состояние.
Для этой цели используем условие Максвелла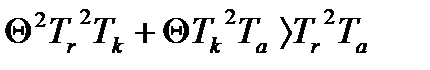
Чтобы изменить параметры регулятора изменим численное значение одного из компонентов уравнения. Либо 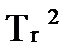, либо 
.
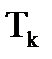В данном примере заменяем .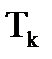
Вместо цифрового значения 1 присваиваем ему значение 0,002.
Отсюда, подставив новое значение 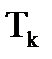в условие Максвелла, имеем:
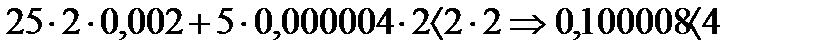
Мы изменили параметры регулятора и перевели систему в другое качественное состояние.
Графики 2
После изменения числовых данных величины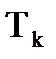
|
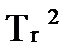
| 2 |
|
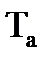
| 2 |
|
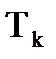
| 0,002 |
|
| 5 |
| -1<f<1 | 1 |
| Время выполнения. | 5000 |
| Шаг | 0,01 |
| Фазовый портрет. Время наблюдения | 90000 |
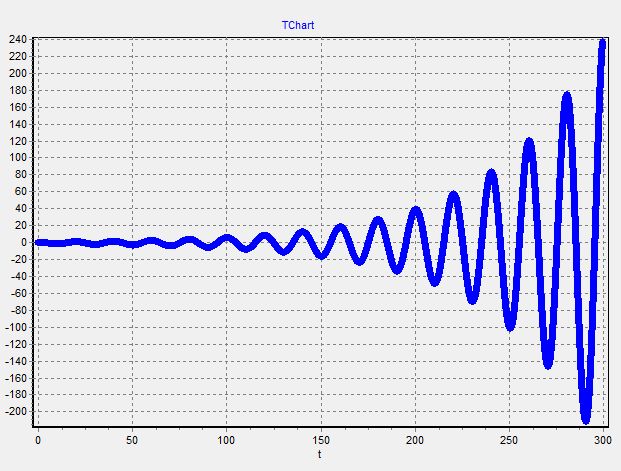
График 2.1
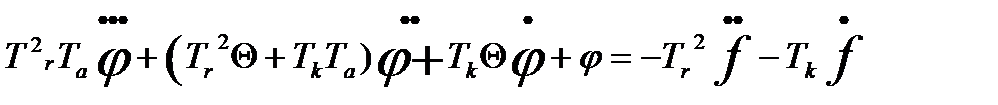
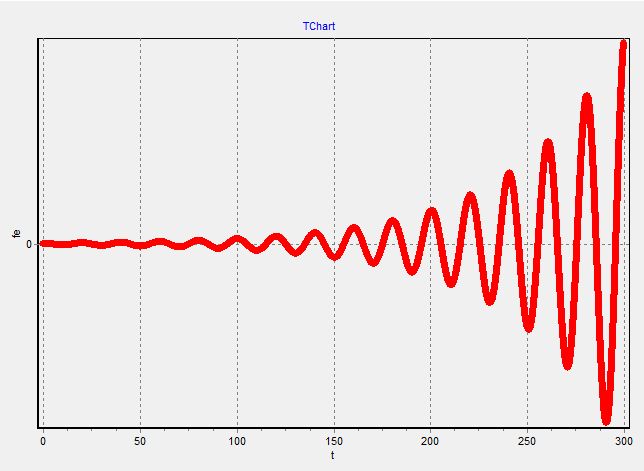
График 2.2 
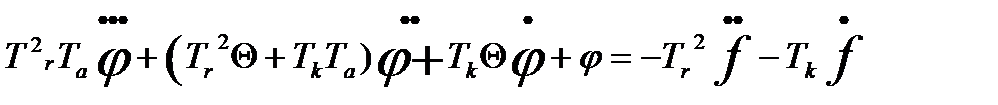
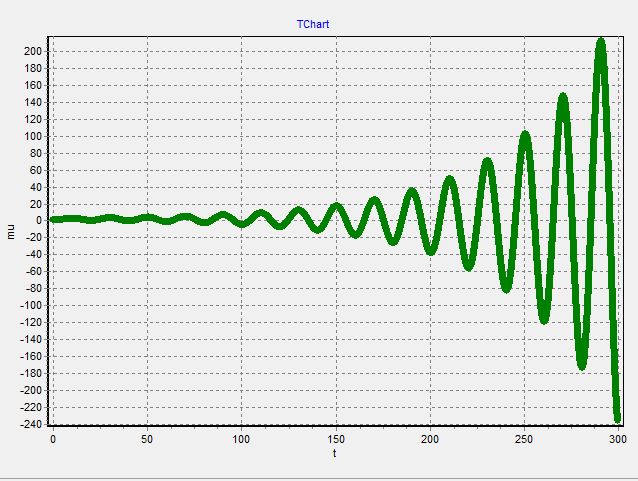
График 2.3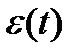 
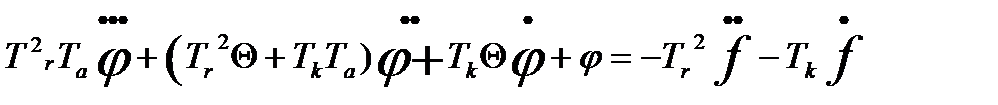
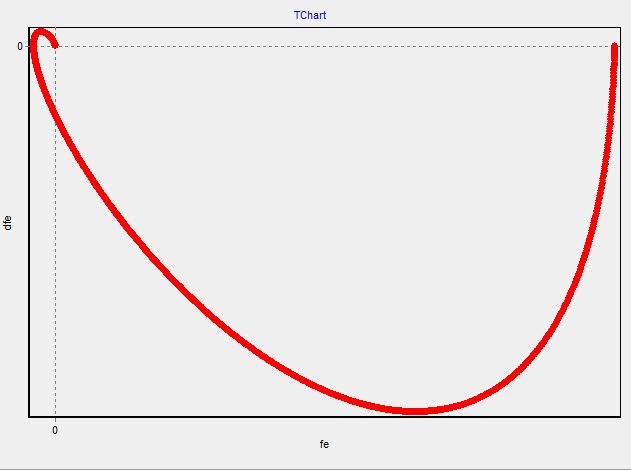
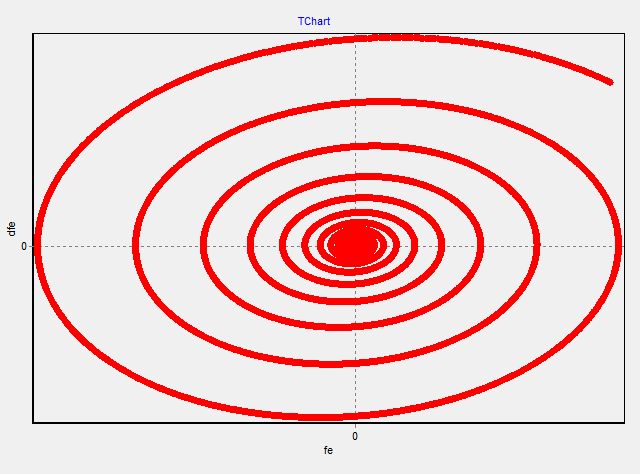
2.4 Фазовый портрет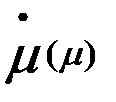
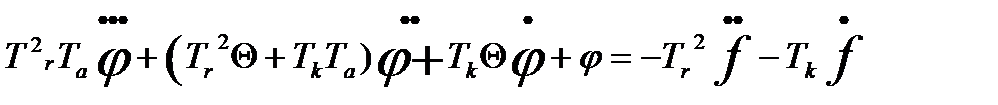
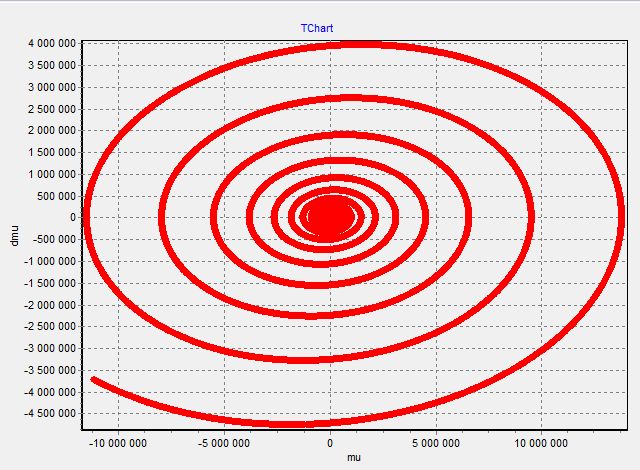
2.5 Фазовый портрет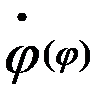
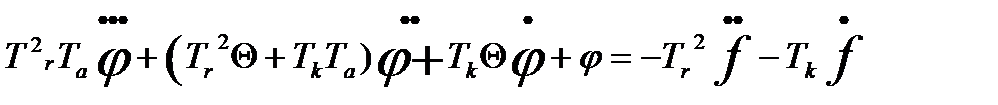
ВЫВОД:
Машина – двигатель управляемая регулятором Ф. Дженкина является устойчивой, так как переходные процессы, в зависимости от различных побудительных причин и параметров на основе предлагаемой математической модели, заканчиваются установившемся режимом и выполняется условие Максвелла.
Как было сказано выше – все фазовые портреты, до изменения параметров регулятора, закручиваются по часовой стрелке, что также говорит об устойчивости системы.
При изменении демпфирующих свойств системы, переходный процесс не заканчивается установившемся режимом, и система становится не устойчивой, хотя фазовые портреты свидетельствуют об обратном, так как закручиваются по часовой стрелке.