Решение дифференциального уравнения

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Уравнение вынужденного движения (1) имеет вид:

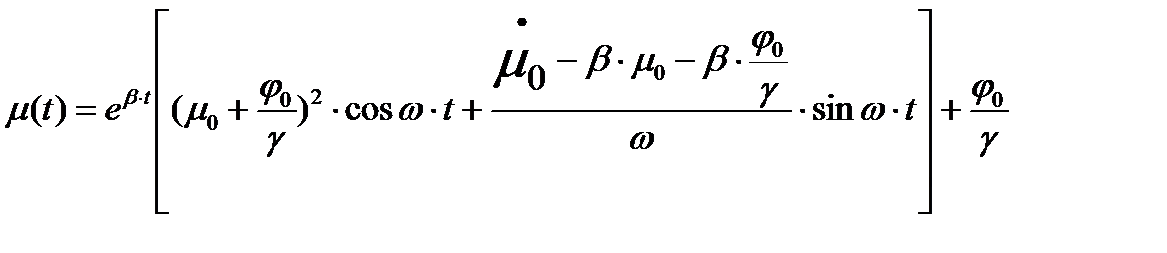
Где

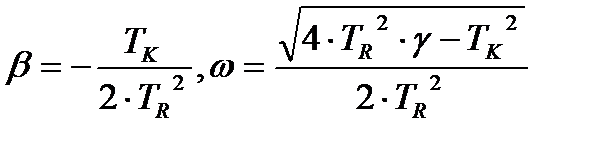
вещественная и мнимая части комплексных сопряженных корней λ1,2 =β±jω характеристического уравнения

Tr² ∙λ²+T_k ∙λ²+γ=0.

СТРУКТУРНАЯ СХЕМА

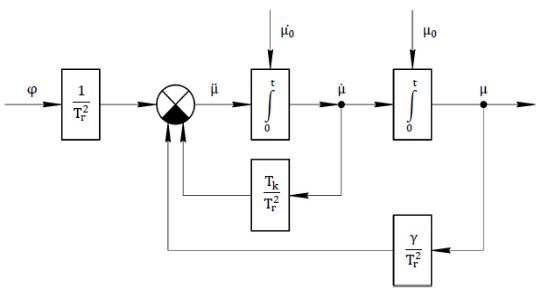
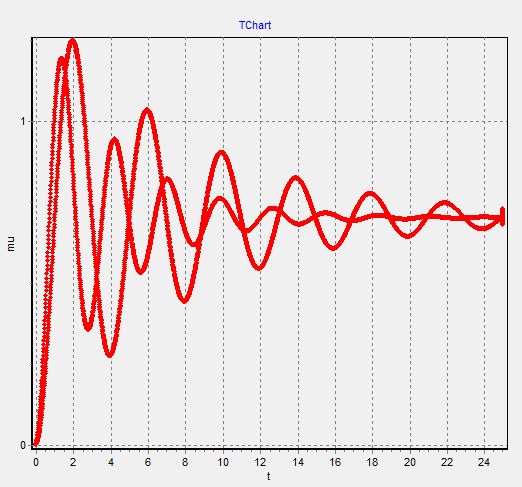
ГРАФИКИ

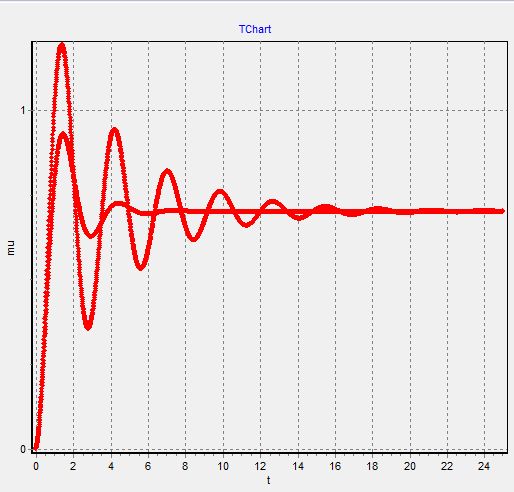
Снимаем наши графики при данных:

Tr²=2

T _k =1

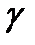=10

График 1

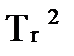
	2
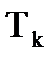
	1
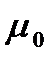
	0
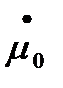
	0
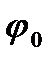
	0,5
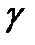
	10
Время набл.	25сек
Шаг	0,01
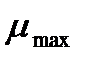
	10

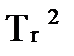
	2
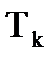
	1
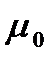
	0
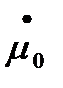
	0
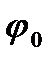
	1,5
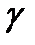
	10
Время набл.	25сек
Шаг	0,01
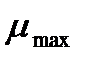
	10

До изменения 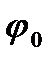После изменения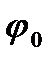

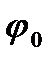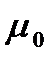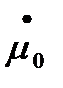1. График μ(t)−изменяем при = =0

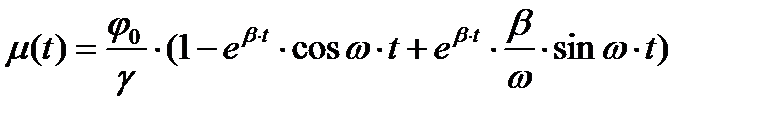
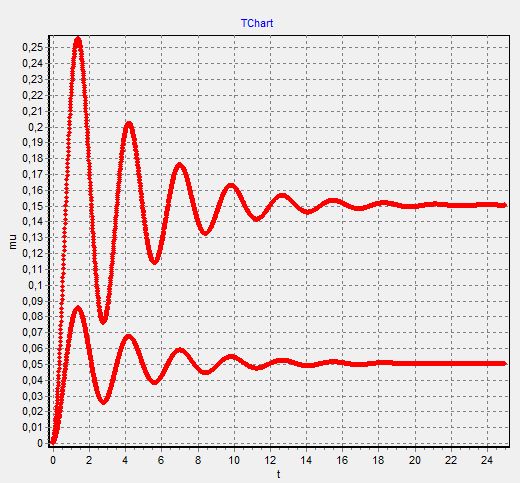
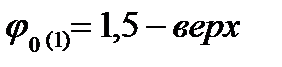
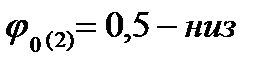
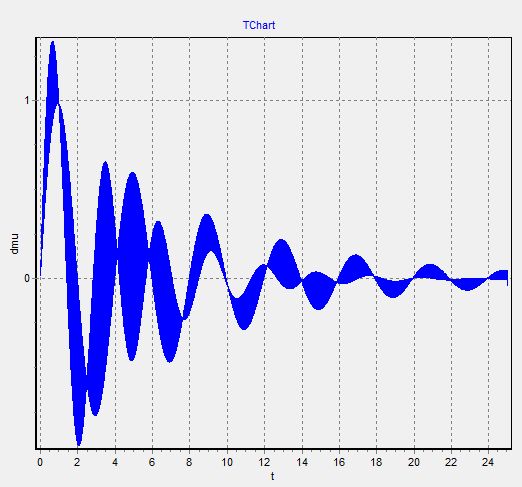
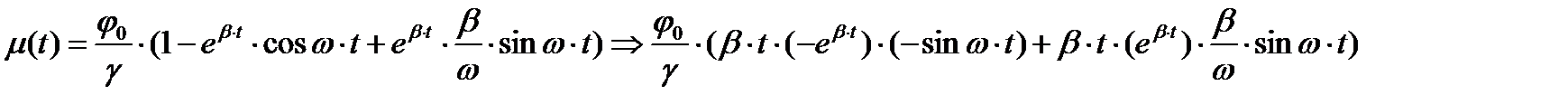Так как при составлении графиков, они сливаются друг с другом (видимо, ошибка программы), то мы строим графики раздельно

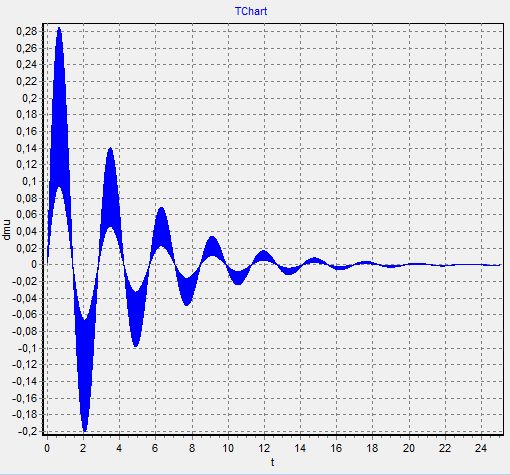
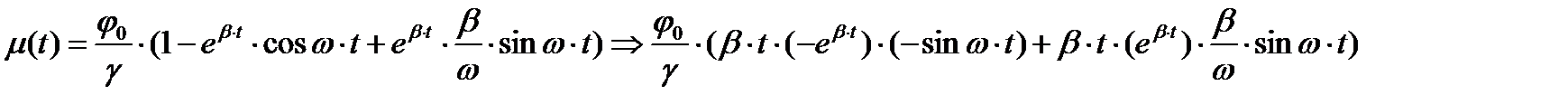
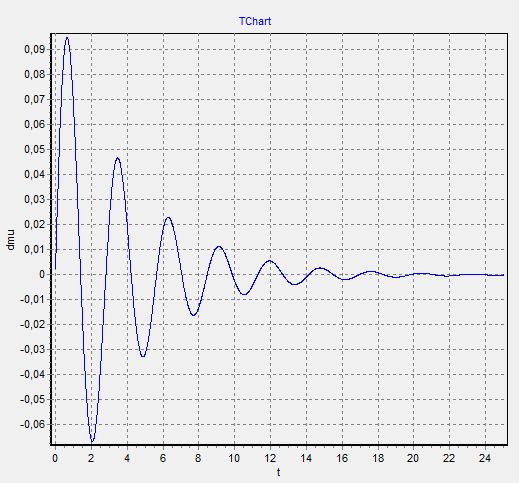
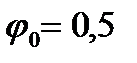
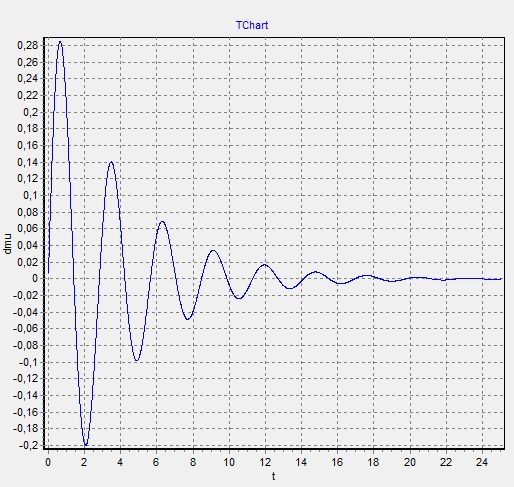
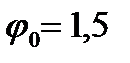
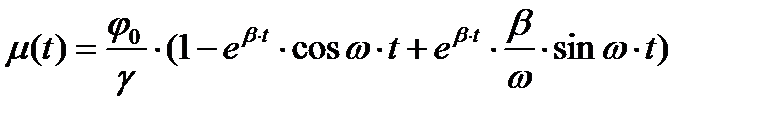
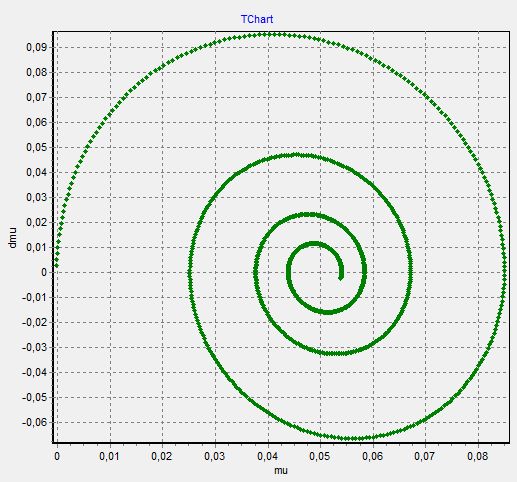
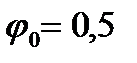
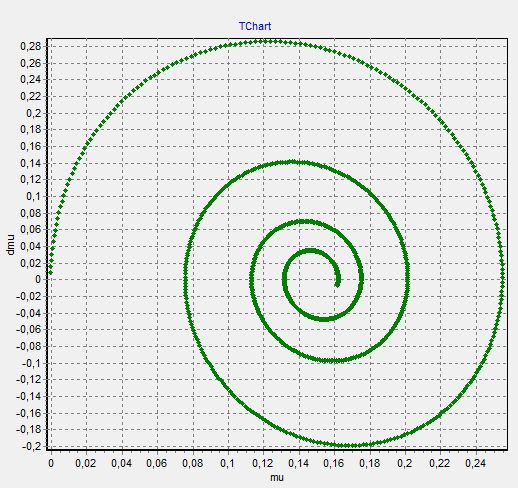
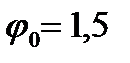
График 2

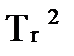
	2
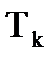
	1
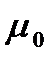
	3
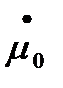
	0
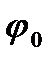
	0
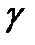
	10
Время набл.	25 сек
Шаг	0,01
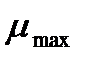
	10

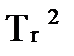
	2
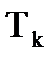
	1
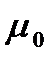
	4
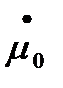
	0
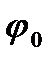
	0
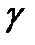
	10
Время набл.	25 сек
Шаг	0,01
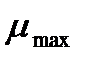
	10

До изменения 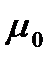После изменения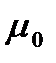

2. График 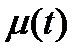- изменяем 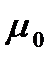при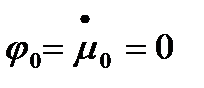

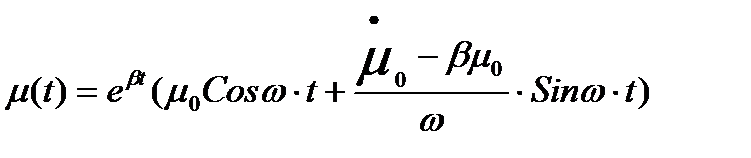
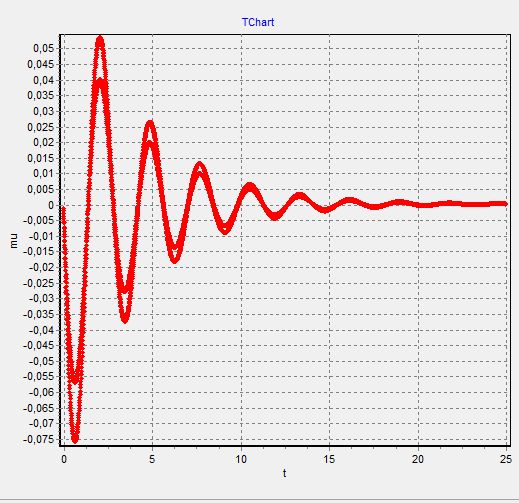
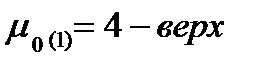
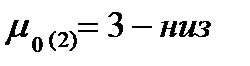
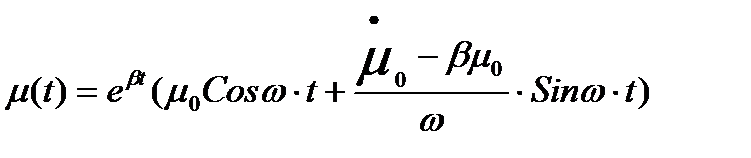
Так как при создании графиков они накладываются друг на друга, как в пунке 1

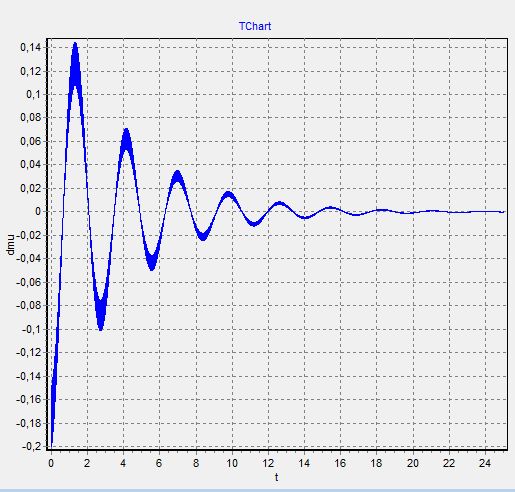
То в таком случае, мы делаем графики отдельно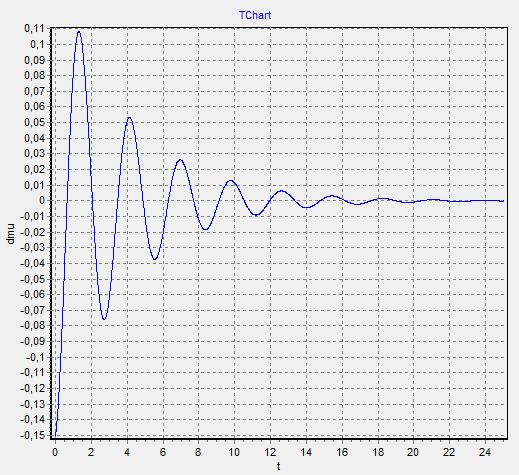

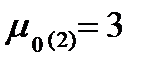
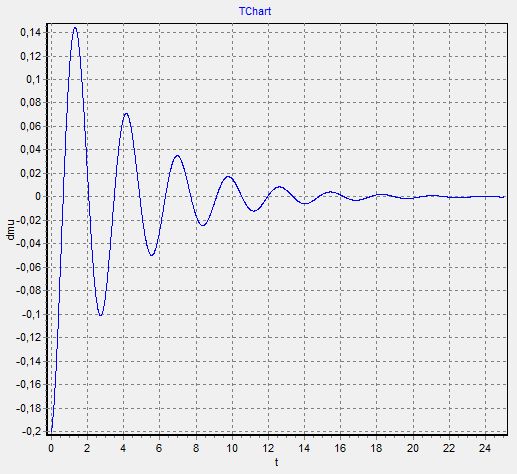
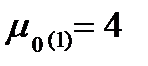
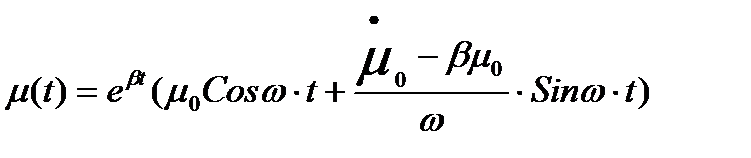
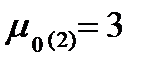
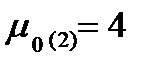
График 3

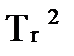
	2
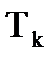
	1
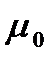
	0
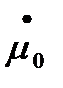
	3
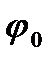
	0
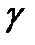
	10
Время набл.	25 сек
Шаг	0,01
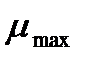
	10

До изменения 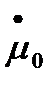После изменения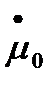

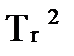
	2
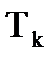
	1
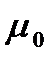
	0
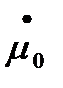
	4
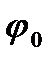
	0
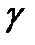
	10
Время набл.	25 сек
Шаг	0,01
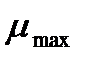
	10

3. График 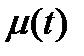- изменяем 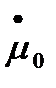при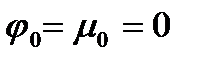

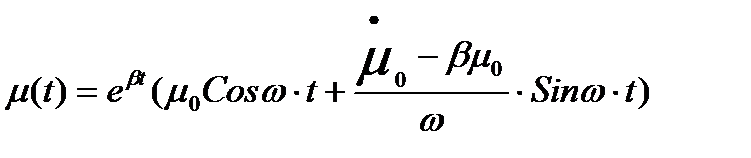
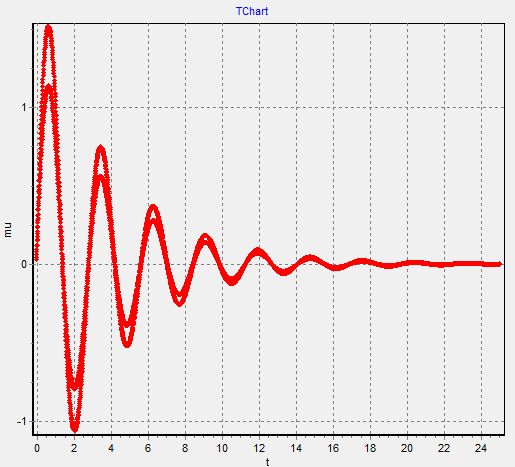
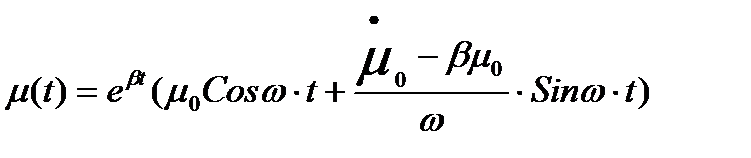
Так как при создании графиков они накладываются друг на друга, к ак в предыдущих пунктах

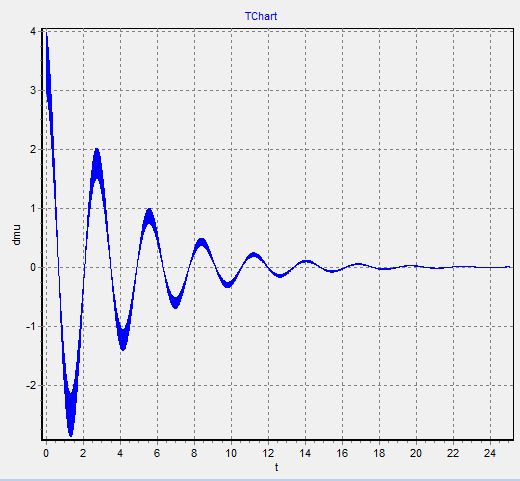
То в таком случае, мы чертим графики отдельно

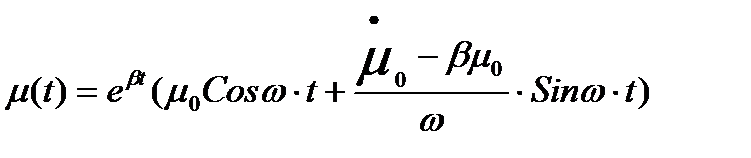
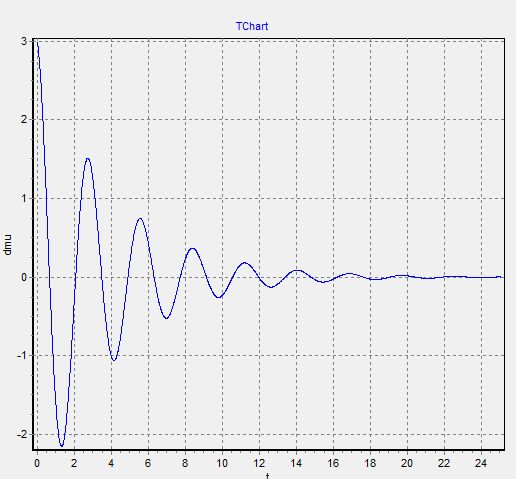
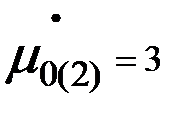
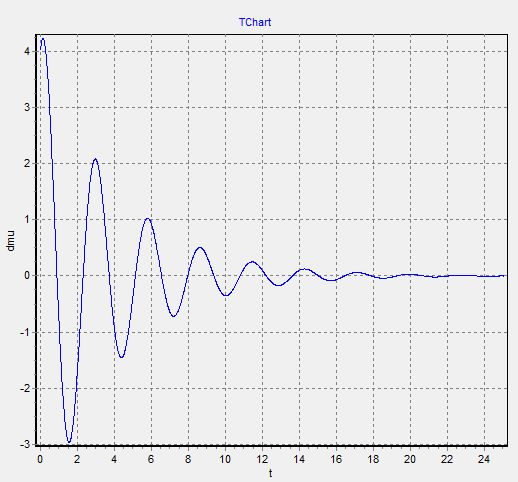
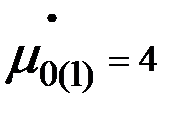
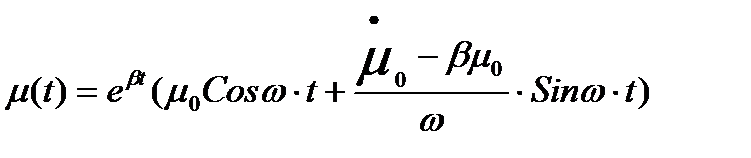
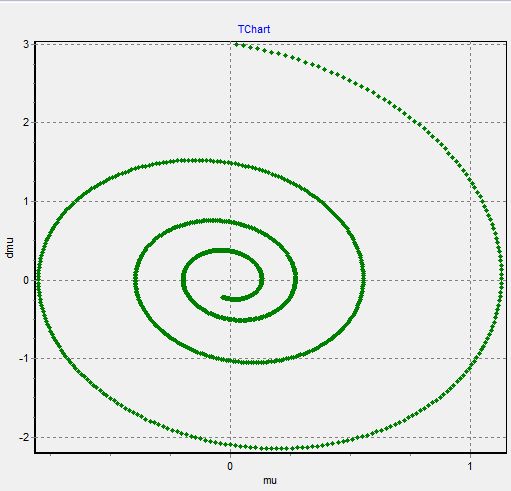
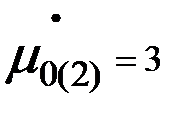
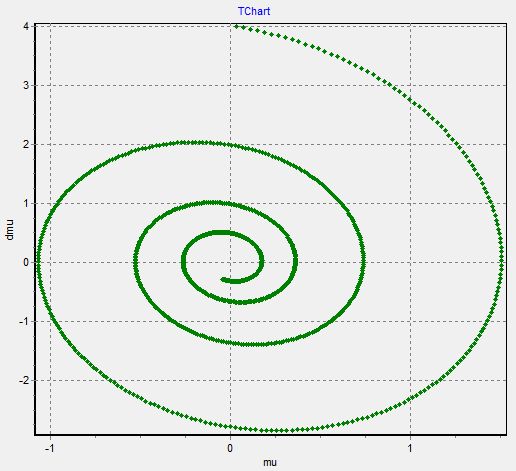
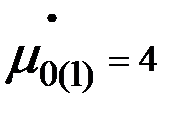
График 4

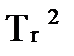
	2
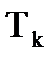
	1
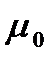
	0
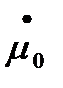
	0
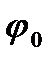
	7
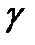
	10
Время набл.	25 сек
Шаг	0,01
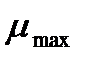
	10

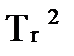
	4
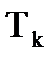
	1
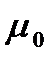
	0
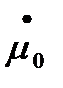
	0
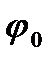
	7
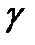
	10
Время набл.	25 сек
Шаг	0,01
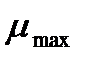
	10

До изменения 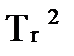После изменения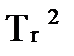

4. График 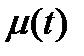- изменяем 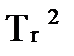при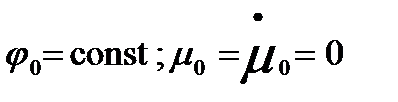

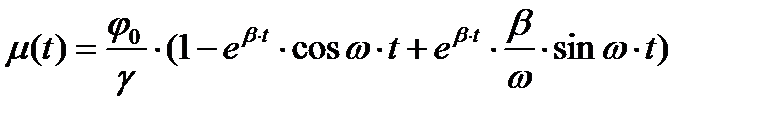
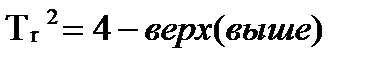
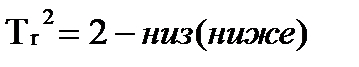
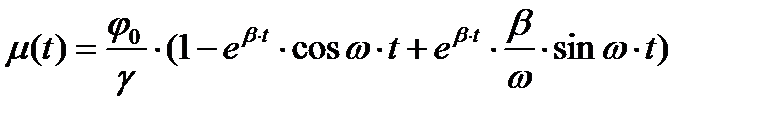
Так как при создании графиков они накладываются друг на друга, к ак в предыдущих пунктах

То в таком случае, мы чертим графики отдельно

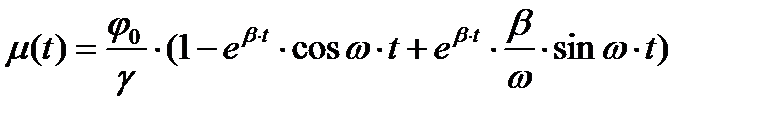
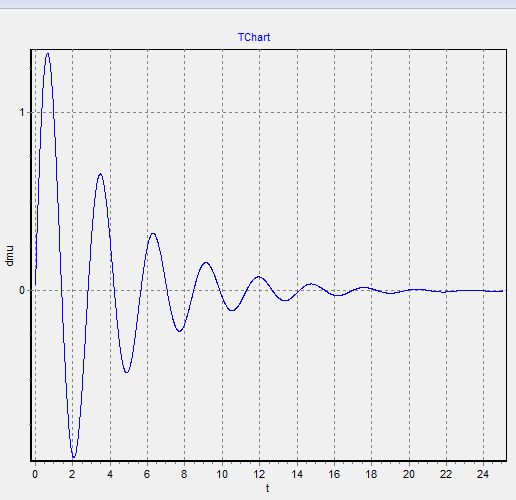
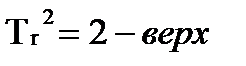
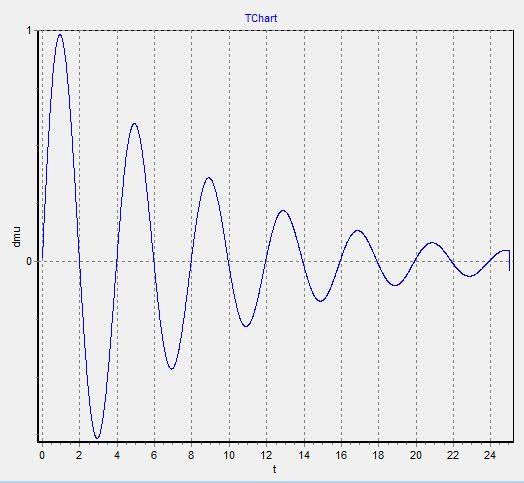
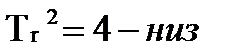
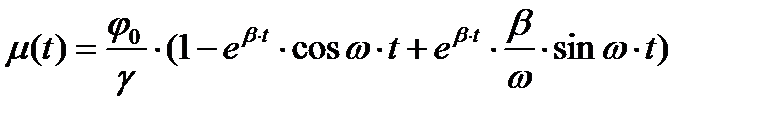
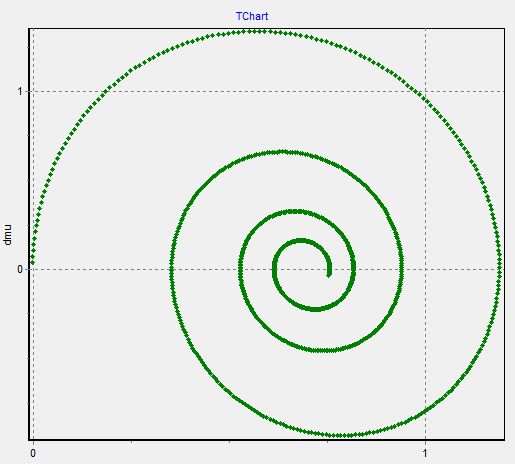
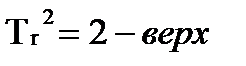
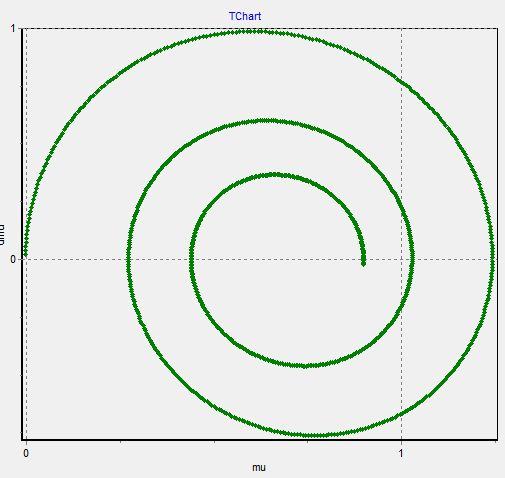
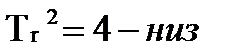
График 5

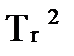
	2
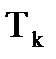
	1
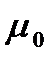
	0
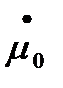
	0
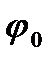
	7
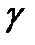
	10
Время набл.	25 сек
Шаг	0,01
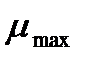
	10

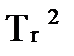
	2
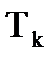
	3
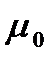
	0
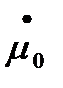
	0
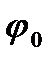
	7
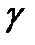
	10
Время набл.	25 сек
Шаг	0,01
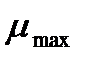
	10

До изменения 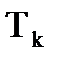После изменения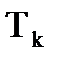

5. График 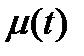- изменяем 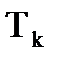при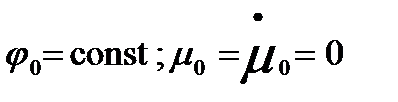

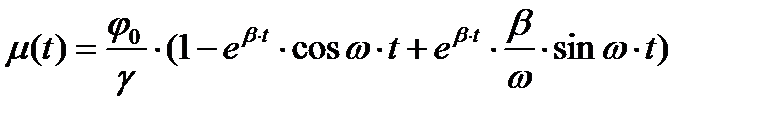
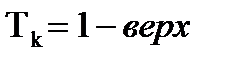
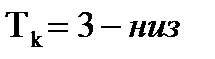
Так как при создании графиков они накладываются друг на друга, как в предыдущих пунктах

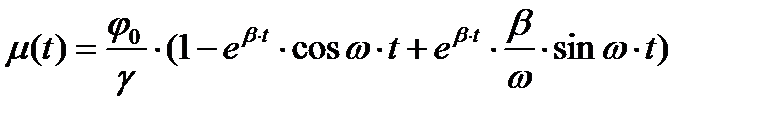
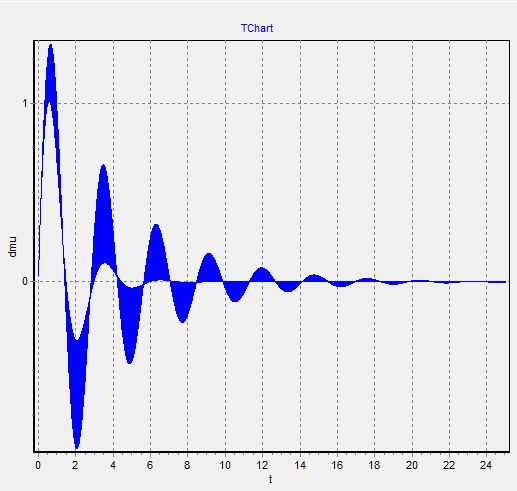
То в таком случае, мы чертим графики отдельно

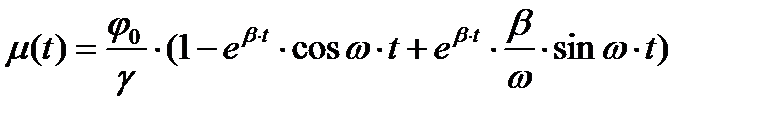
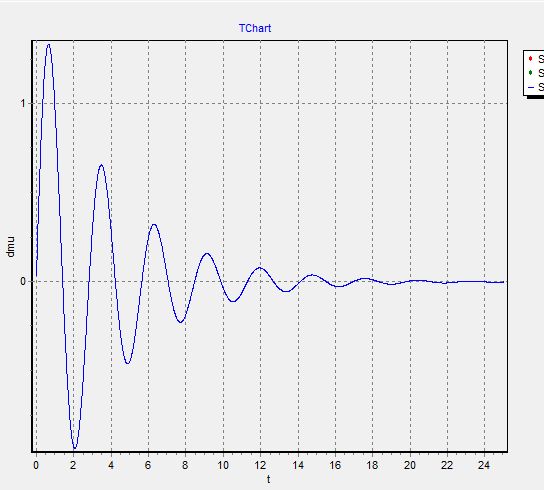
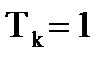
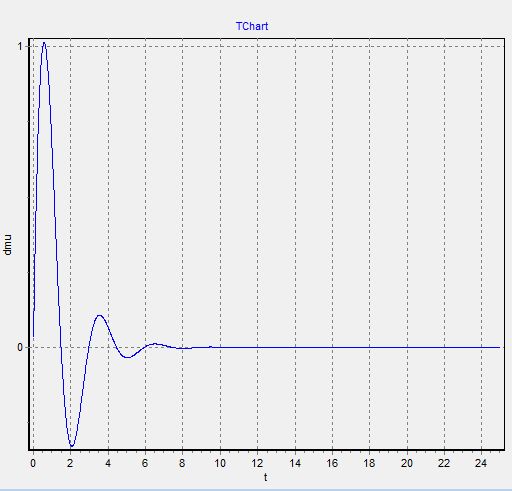
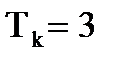
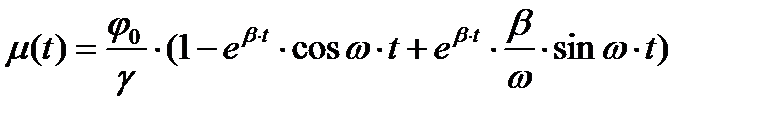
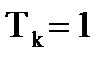
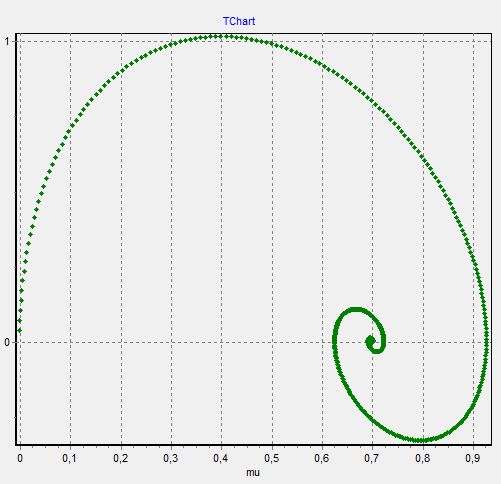
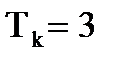
График 6

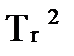
	2
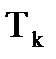
	1
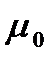
	0
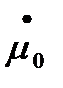
	0
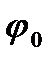
	7
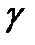
	10
Время набл.	25 сек
Шаг	0,01
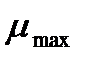
	10

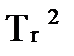
	2
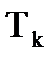
	1
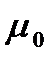
	0
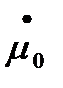
	0
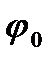
	7
	15
Время набл.	25 сек
Шаг	0,01
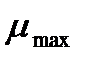
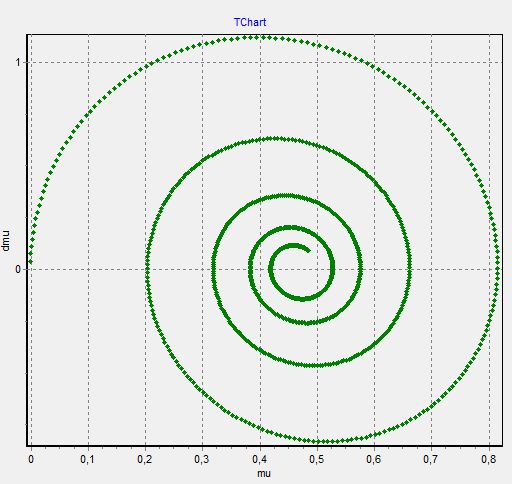
	10

До изменения 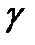После изменения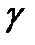

6. График 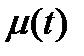- изменяем 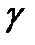при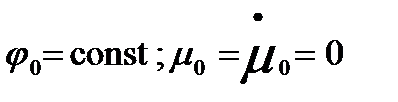

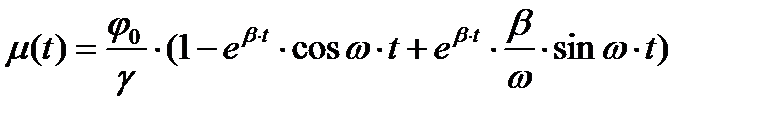
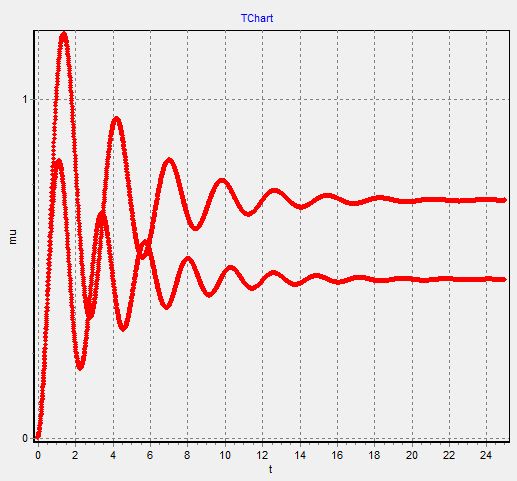
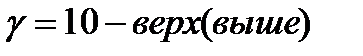
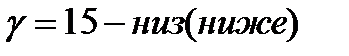
Так как при создании графиков они накладываются друг на друга, как в предыдущих пунктах

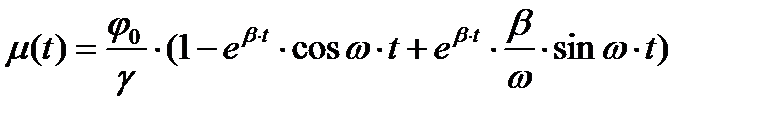
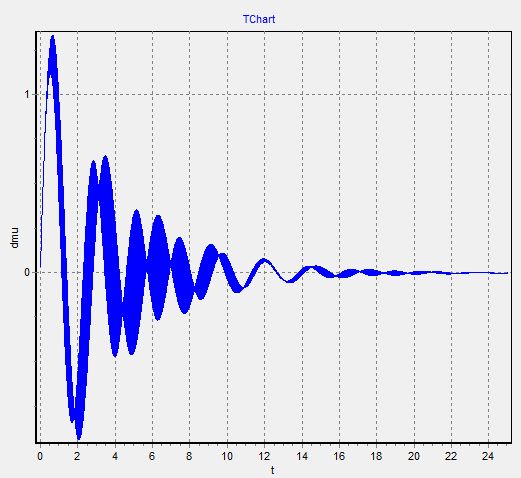
То в таком случае, мы чертим графики отдельно

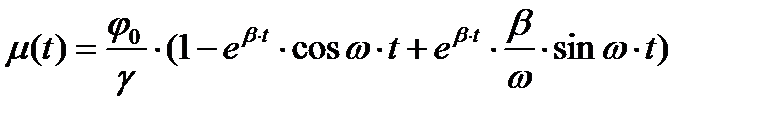
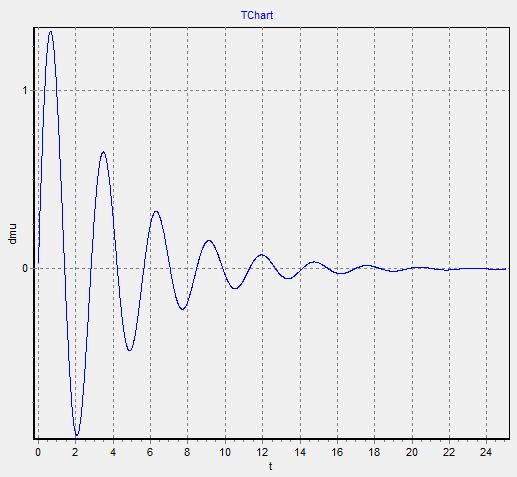
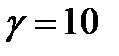
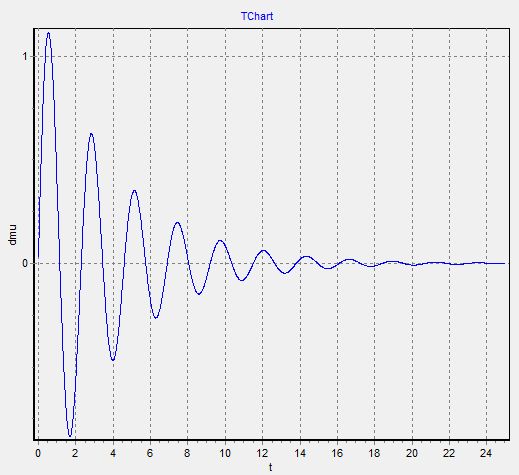
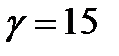
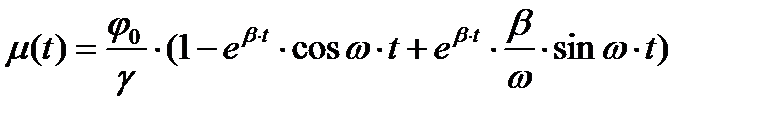
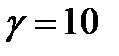
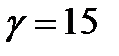
ВЫВОД:

Динамика регулятора Дж.Уатта является устойчивой, так как переходные процессы, в зависимости от различных побудительных причин и параметров на основе предлагаемой математической модели, заканчиваются установившимся режимом.

За исключением графиков №2 и №3, так как отсутствует внешнее воздействие.