Исследование динамики регулятора Ф. Дженкина.

Дата: 2025-05-01; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

СПБГМТУ

Кафедра судовой автоматики и измерений

Лаборатория моделирования динамических систем

Лабораторная работа №2

Исследование динамики регулятора Ф. Дженкина.

по дисциплине

«Теория автоматического управления»

Выполнил:

Студент группы №5340

Беляков Михаил Юрьевич

Проверил:

Ассистент

Фёдорова Ольга Игоревна

Санкт – Петербург

2018 год

Оглавление

Цель работы ...........................................................3

Дифференциальное уравнение.............................3

Решение дифференциального уравнения............3

Структурная схема .................................................4

Графики...................................................................5

1. График μ(t)−изменяем φ0 при μ0̇=μ0=0............5

2. График μ(t)−изменяем μ0 при φ0=μ0̇=0 ...........7

3. График μ(t)−изменяем μ0̇ при φ0=μ0=0 .......... 9

4. График μ(t)−изменяем Tr2 при φ0=const,μ0̇=μ0=0 ................................................11

5. График μ(t)−изменяем Tk при φ0=const,μ0̇=μ0=0 ................................................13

ЦЕЛЬ РАБОТЫ

Изучение динамики регулятора Ф. Дженкина с помощью переходных процессов (временных характеристик) в зависимости от каждой из побудительных причин и параметров регулятора.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ

Математической моделью (дифференциальной математической моделью) регулятора является выражение

Tr²∙μ̈+T _k ∙μ̇= j (1), где

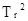- - коэффициент, характеризующий инерционные свойства регулятора, [сек ²];

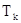− - коэффициент, характеризующий демпфирующие свойства, [сек];

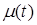- - регулирующее воздействие на объект регулирования (выходной сигнал регулятора);

- μ̇(t) – первая производная от 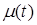(скорость регулирующего воздействия);

- μ̈(t) - вторая производная от 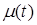(ускорение регулирующего воздействия);

- j(t) – регулируемая величина объекта (выходной сигнал регулятора);

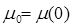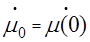- , - начальные отклонения от некоторого состояния равновесия (невозмущённого движения);

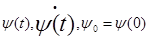- - промежуточная переменная, её скорость и начальное отклонение.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Уравнение вынужденного движения (1) имеет вид:

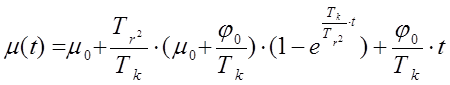(2)

СТРУКТУРНАЯ СХЕМА

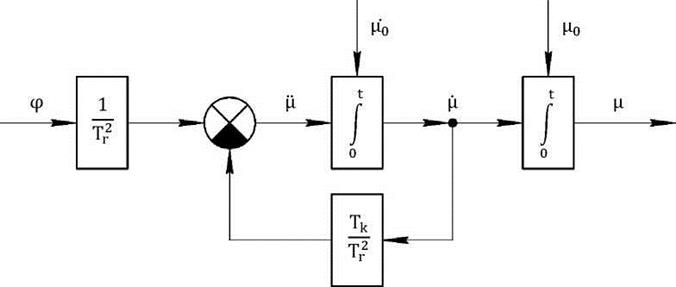
ГРАФИКИ

Снимаем наши графики при данных:

Tr²=2

T _k =1

График 1

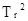
	2
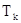
	1
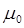
	0
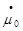
	0
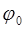
	0,5
Время набл.	20 сек
Шаг	0,01
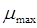
	10

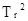
	2
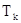
	1
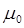
	0
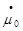
	0
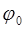
	0,5
Время набл.	20 сек
Шаг	0,01
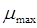
	10

До изменения 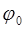После изменения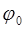

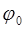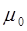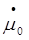1. График μ(t)−изменяем при = =0

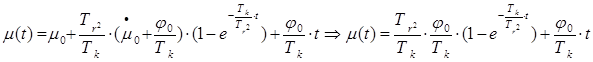
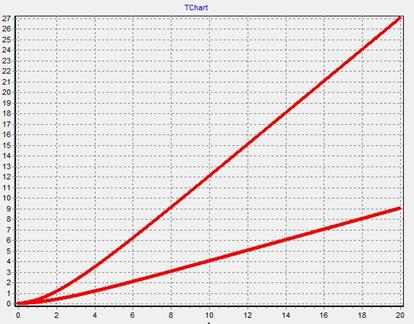
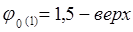
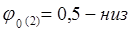
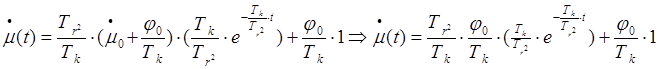
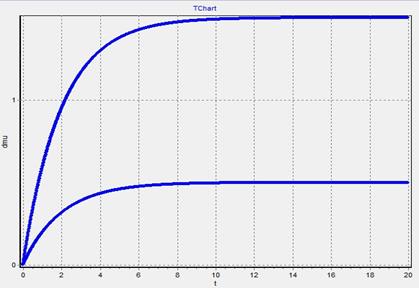
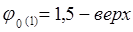
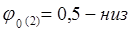
График 2

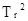
	2
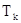
	1
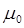
	3
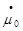
	0
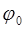
	0
Время набл.	20 сек
Шаг	0,01
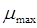
	10

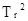
	2
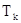
	1
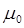
	4
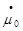
	0
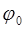
	0
Время набл.	20 сек
Шаг	0,01
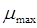
	10

До изменения 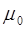После изменения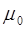

График 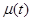- изменяем 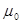при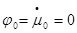

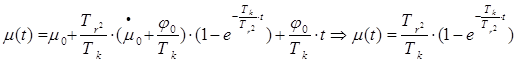
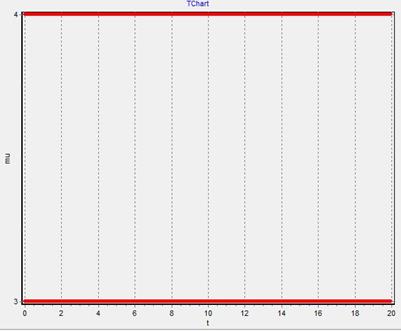
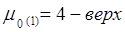
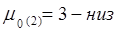
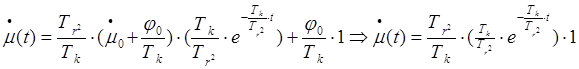
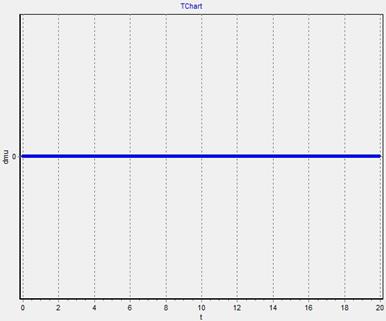
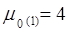
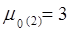
График 3

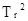
	2
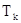
	1
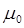
	0
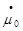
	3
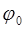
	0
Время набл.	20 сек
Шаг	0,01
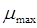
	10

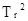
	2
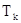
	1
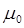
	0
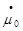
	4
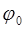
	0
Время набл.	20 сек
Шаг	0,01
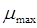
	10

До изменения 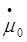После изменения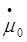

График 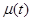- изменяем 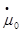при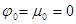

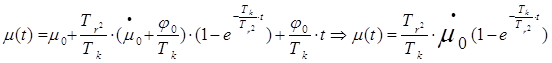
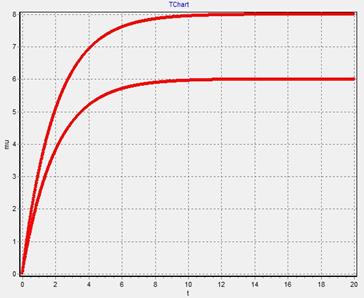
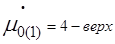
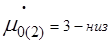
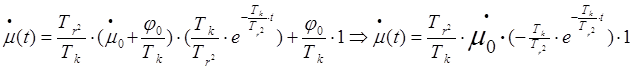
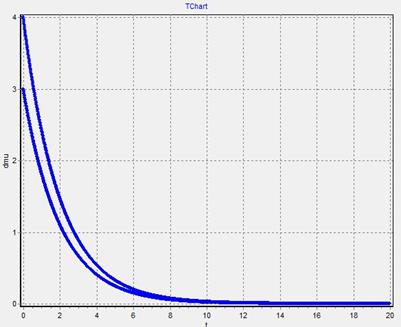
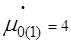
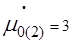
График 4

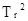
	2
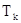
	1
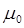
	0
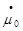
	0
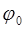
	7
Время набл.	20 сек
Шаг	0,01
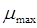
	10

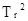
	4
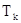
	1
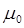
	0
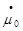
	0
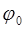
	7
Время набл.	20 сек
Шаг	0,01
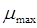
	10

До изменения 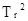После изменения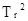

4. График 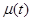- изменяем 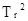при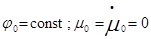

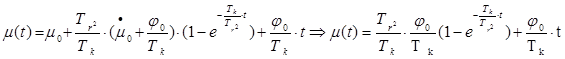
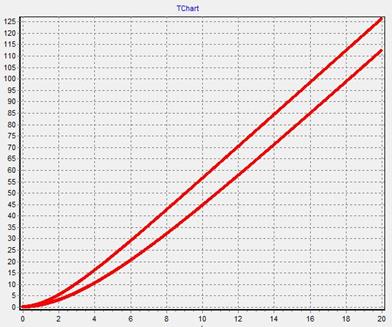
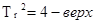
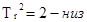
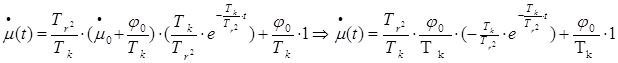
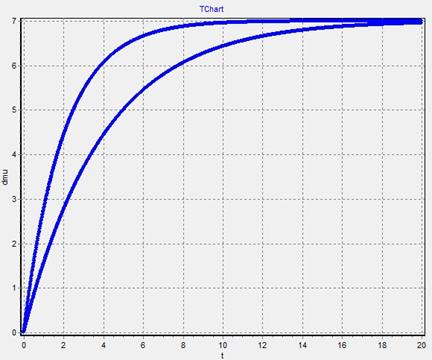
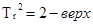
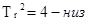
График 5

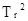
	2
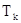
	1
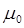
	0
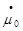
	0
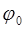
	7
Время набл.	20 сек
Шаг	0,01
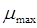
	10

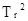
	2
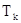
	3
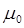
	0
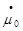
	0
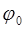
	7
Время набл.	20 сек
Шаг	0,01
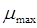
	10

До изменения 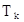После изменения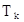

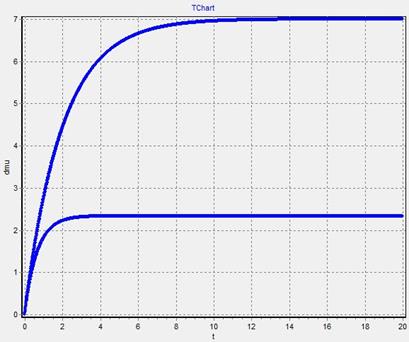
5. График 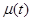- изменяем 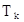при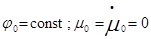

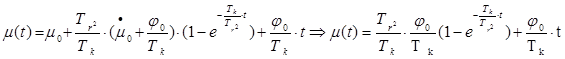
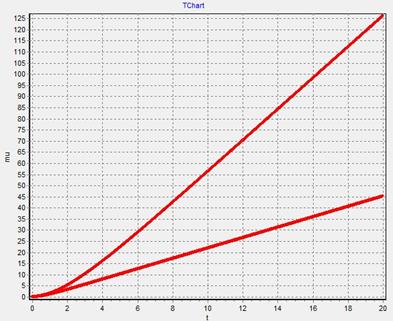
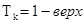
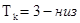
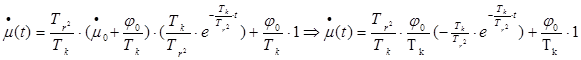
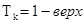
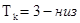
ВЫВОД:

Регулятор Ф. Дженкина это статический регулятор, при котором регулируемая величина принимает точное значение в установившемся режиме и не зависит от величины возмущающего фактора.