Лабораторная работа №11. Основы алгоритмизации.
1. линейный алгоритм
Упражнение 1. Найти сумму двух данных чисел.
Дано: a, b — слагаемые.
Требуется: sum — сумма значений а и b.
Метод решения: sum = a + b.
Словесная форма алгоритма:
Запросить значение переменной а
Запросить значение переменной b
Записать в переменную sum значение выражения a + b
Вывести на печать значение переменной sum
Блок-схема:
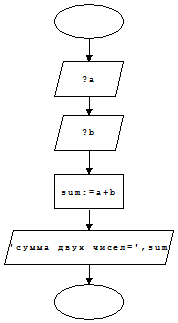
Анализ полученных результатов.
1. а = 4; b = 10. sum = 14.
2. а = –10; b = –11. sum = –21.
3. а = 45; b=10,5. sum=55,5.
Упражнение 2. Даны два числа, являющихся величинами катетов некоторого прямоугольного треугольника. Вычислить длину гипотенузы этого треугольника.
Дано: x и y — катеты прямоугольного треугольника.
Требуется: z — гипотенуза прямоугольного треугольника.
Метод решения: z = 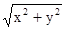 .
.
Словесная форма алгоритма:
Запросить значение переменной x
Запросить значение переменной y
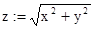 .
.
Вывести значение переменной z
Блок-схема:
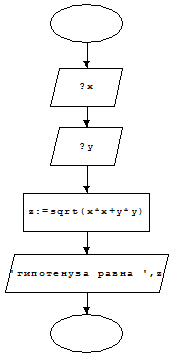
Анализ полученных результатов.
1. x = 3; y = 4. z = 5.
2. x = 11; y = 12. z = 16,28.
3. x = 25; y=30. z=39,05.
2. разветвляющийся алгоритм
упражнение 3. Найти максимум из двух чисел.
Дано: a, b — заданные числа.
Требуется: max — максимум из чисел а и b.
Метод решения: если a>b, то max присвоить a, иначе b.
Словесная форма записи алгоритма:
Запросить значение переменной a
Запросить значение переменной b
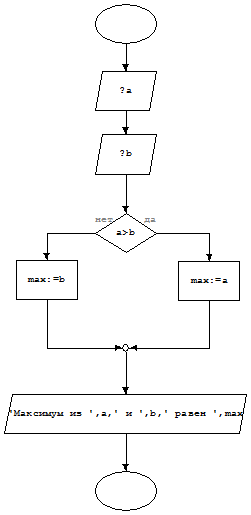
Анализ полученных результатов.
a = 3; b = 4. max = 4.
a = 11; b = 2. max =11.
a = 25; b=25. max =25.
Упражнение 4 . Найти максимум из трех чисел.
Дано: Переменные a, b, с.
Требуется: max — максимум из чисел а, b, с.
Метод решения. Если a>b, то max:=a, иначе max:=b. Если c>max, то max:=c.
Словесная форма записи алгоритма:
Запросить значение переменной a
Запросить значение переменной b
Запросить значение переменной c
Если a>b, то max := a, иначе max := b
Если c>max, то max := c
Вывести значение переменной max
Блок-схема:
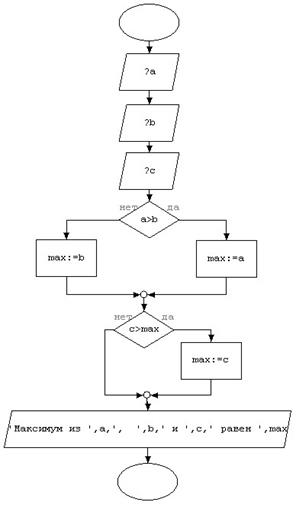
Анализ полученных результатов.
1. а = 4; b = 10; c = 4. max = 10.
2. а = –10; b = 12; c = 1. max = 12.
3. а = 45; b=10,5; c = 14. max=45.
3. циклический алгоритм
Упражнение 5 . Найти сумму первых n натуральных чисел.
Дано: n — количество первых натуральных чисел.
Требуется: S = 1 + 2 + …+ n — сумма первых n натуральных чисел.
Метод решения: Sn = Sn-1 + n.
Словесная форма записи алгоритма:
Запросить значение переменной n
i:=1
S:=0
пока i<=n повторять
S := S+i
i := i+1
Конец цикла
Вывести значение переменной S
Блок-схема:
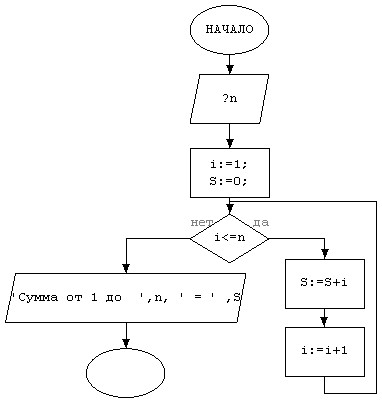
Тестирование алгоритма
Зададим количество суммируемых первых натуральных чисел n = 5. Мы должны получить значение суммы первых пяти натуральных чисел S = 15. Протрассируем алгоритм и запишем значения переменных на каждом шаге в таблицу.
Тело цикла будет выполняться 5 раз.
| № шага | i на входе в тело цикла | S | i на выходе из тела цикла | |
| 1 | 1 | |||
| S := S + i | 0+1 = 1® S | i := i + 1 | 1 +1 = 2 ® i | |
| 2 | 2 | 
| ||
| S := S + i | 1+2 = 3® S | i := i + 1 | 2 +1 = 3 ® i | |
| 3 | 3 | 
| ||
| S := S + i | 3+3 = 6 ® S | i := i + 1 | 3 +1 = 4 ® i | |
| 4 | 4 | 
| ||
| S := S + i | 6+4 = 10® S | i := i + 1 | 4 +1 = 5 ® i | |
| 5 | 5 | 
| ||
| S := S + i | 10+5 = 15® S | i := i + 1 | 5 +1 = 6 ® i |
СРСП №1 0. Основы алгоритмизации.








