Московский государственный технический университет

Дата: 2025-05-01; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Министерство образования Российской Федерации

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. Н.Э. БАУМАНА

Факультет: Информатика и системы управления

Кафедра: Системы автоматического управления(ИУ1)

Лабораторная работа № 2

«Типовые динамические звенья систем автоматического управления»

Преподаватели:

Карпунин А.А.,

Задорожная Н.М.

Студент:

Ромашов В.И.

ИУ8-44

Москва 2015г.

Цель работы: исследование переходных характеристик и динамических свойств типовых звеньев систем автоматического управления.

Порядок выполнения работы:

1) Построить схемы моделирования динамических звеньев:

· усилительного;

· интегрирующего;

· апериодического;

· реального дифференцирующего;

· колебательного;

· консервативного.

2) Осуществить моделирование и снять переходные характеристики типовых динамических звеньев.

3) Определить значение коэффициента затухания ζ для колебательного звена, при котором время переходного процесса будет минимальным.

4) Для начальных данных произвести вариацию параметров типовых звеньев по заданию преподавателя и сделать выводы о влиянии того или иного параметра на переходной процесс системы.

5) Сделать сравнительный анализ результатов моделирования.

Исходные данные (вариант № 17):

Параметры динамических звеньев:

Ход выполнения работы.

Звено	Графики характеристик
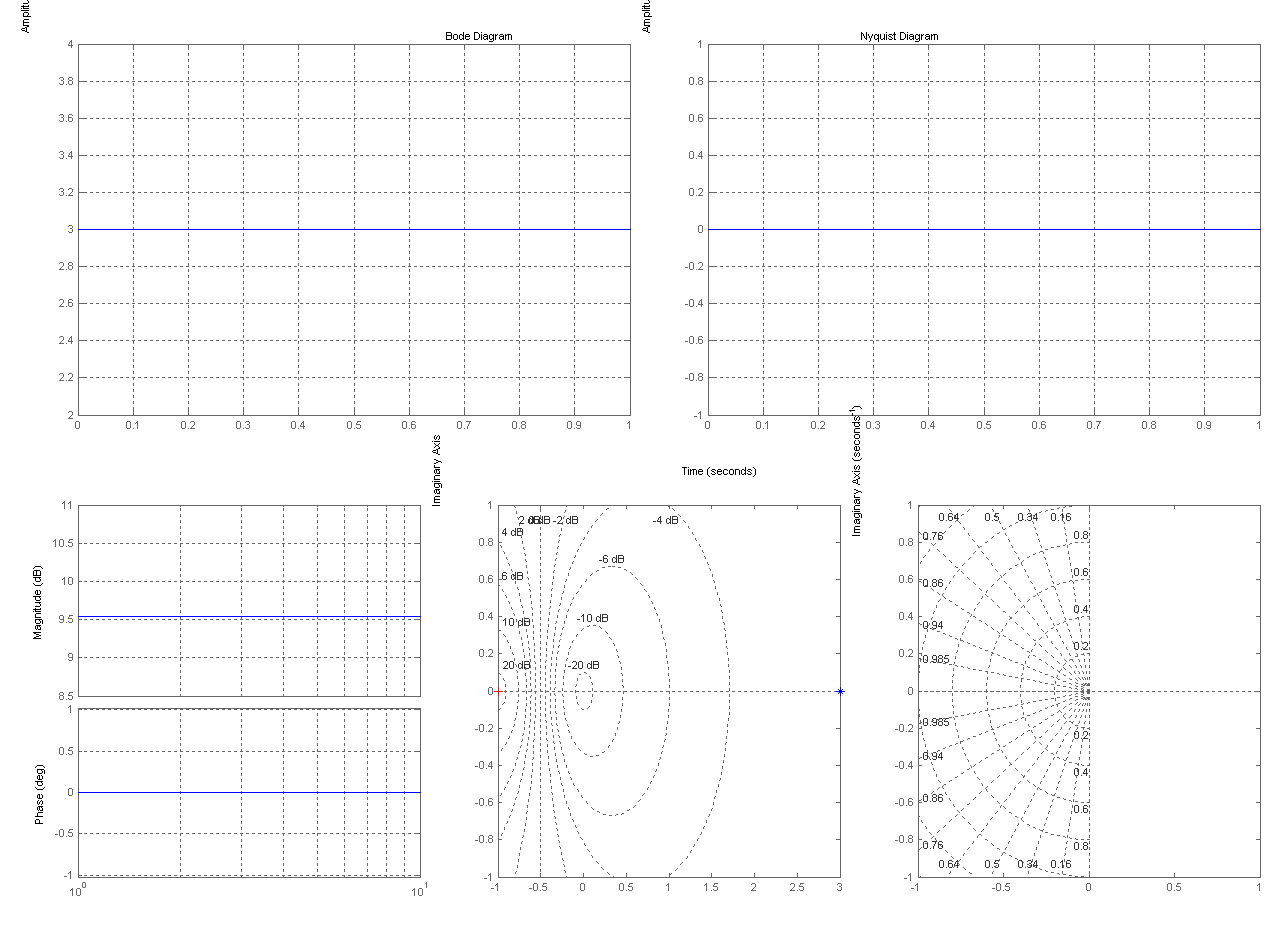
Усилительное звено 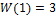    W(1)=tf([k],[1])
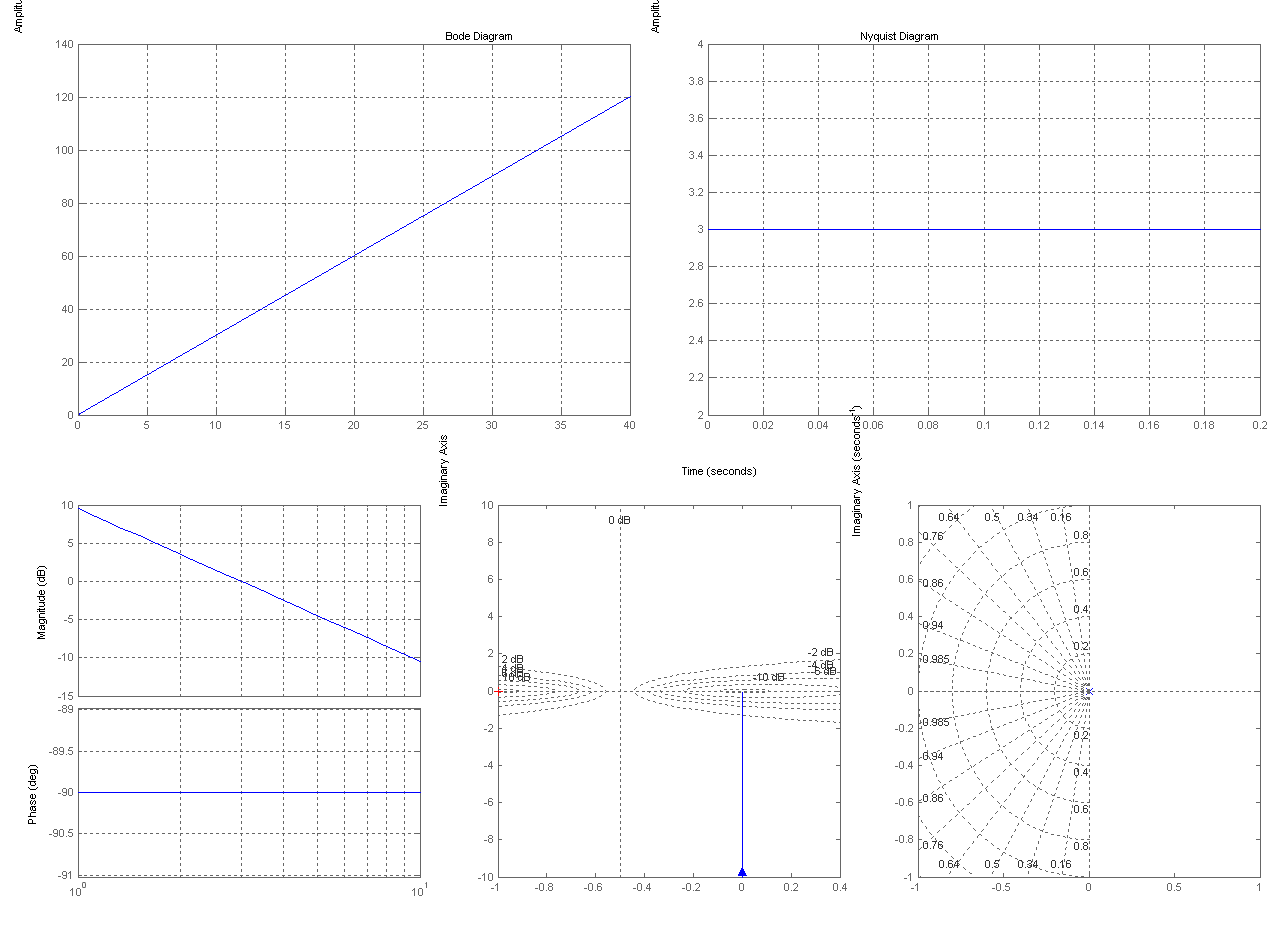
Интегрирующее звено 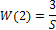    W(2)=tf([k],[1 0])
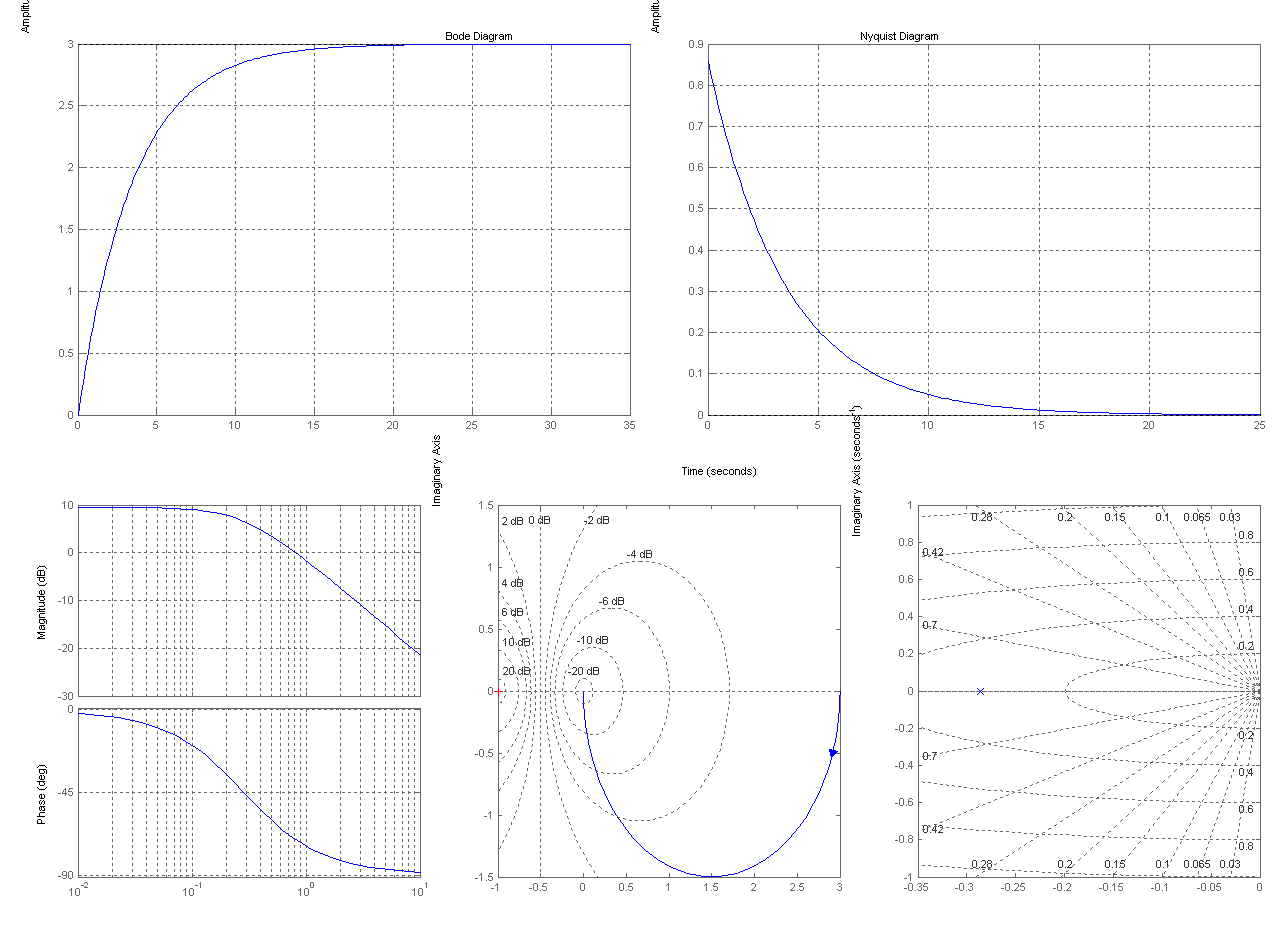
Апериодическое звено 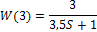    W(3)=tf([k],[T 1])
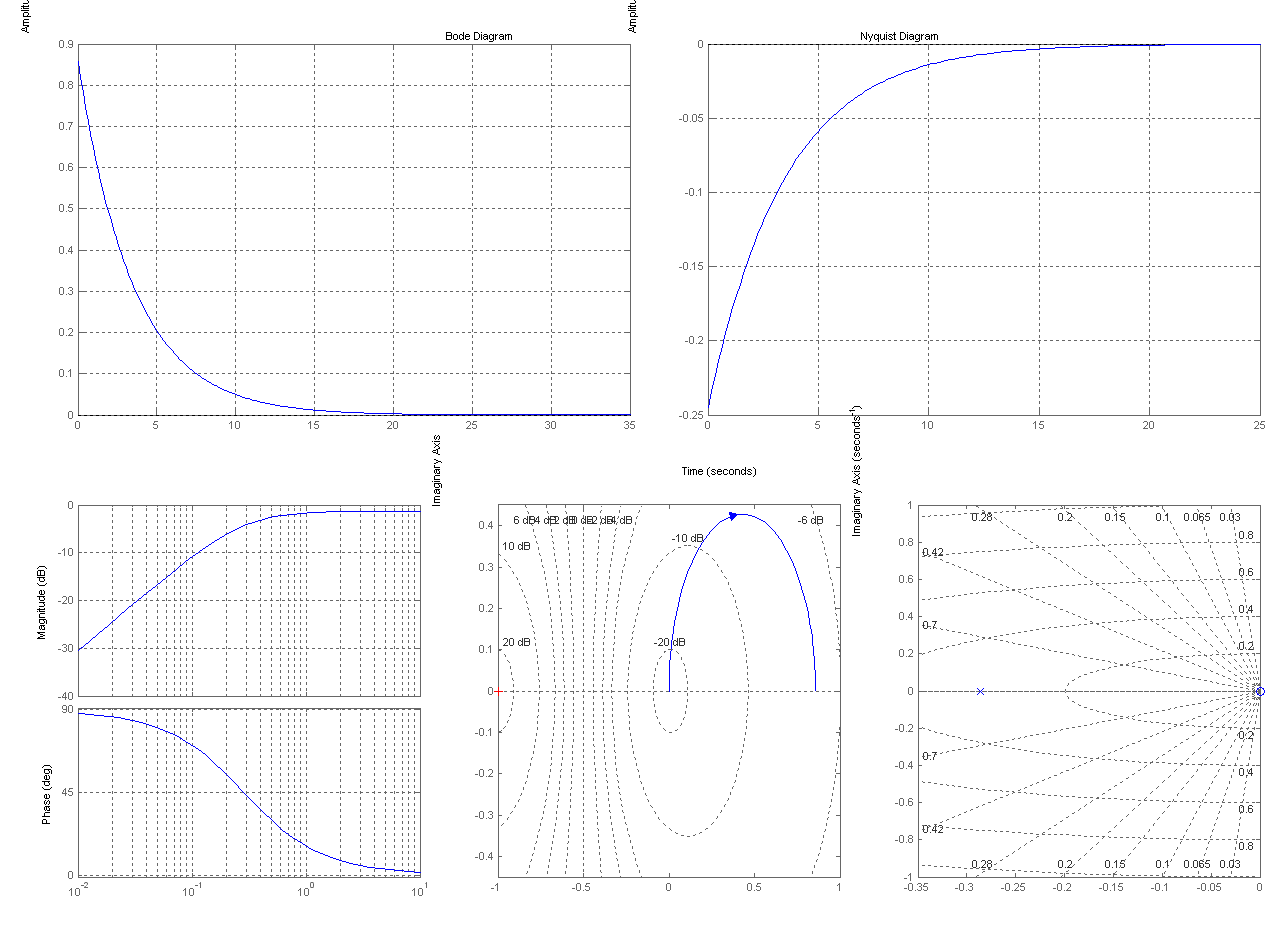
Реальное дифференцирующее звено 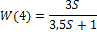    W(4)=tf([k 0], [T 1])
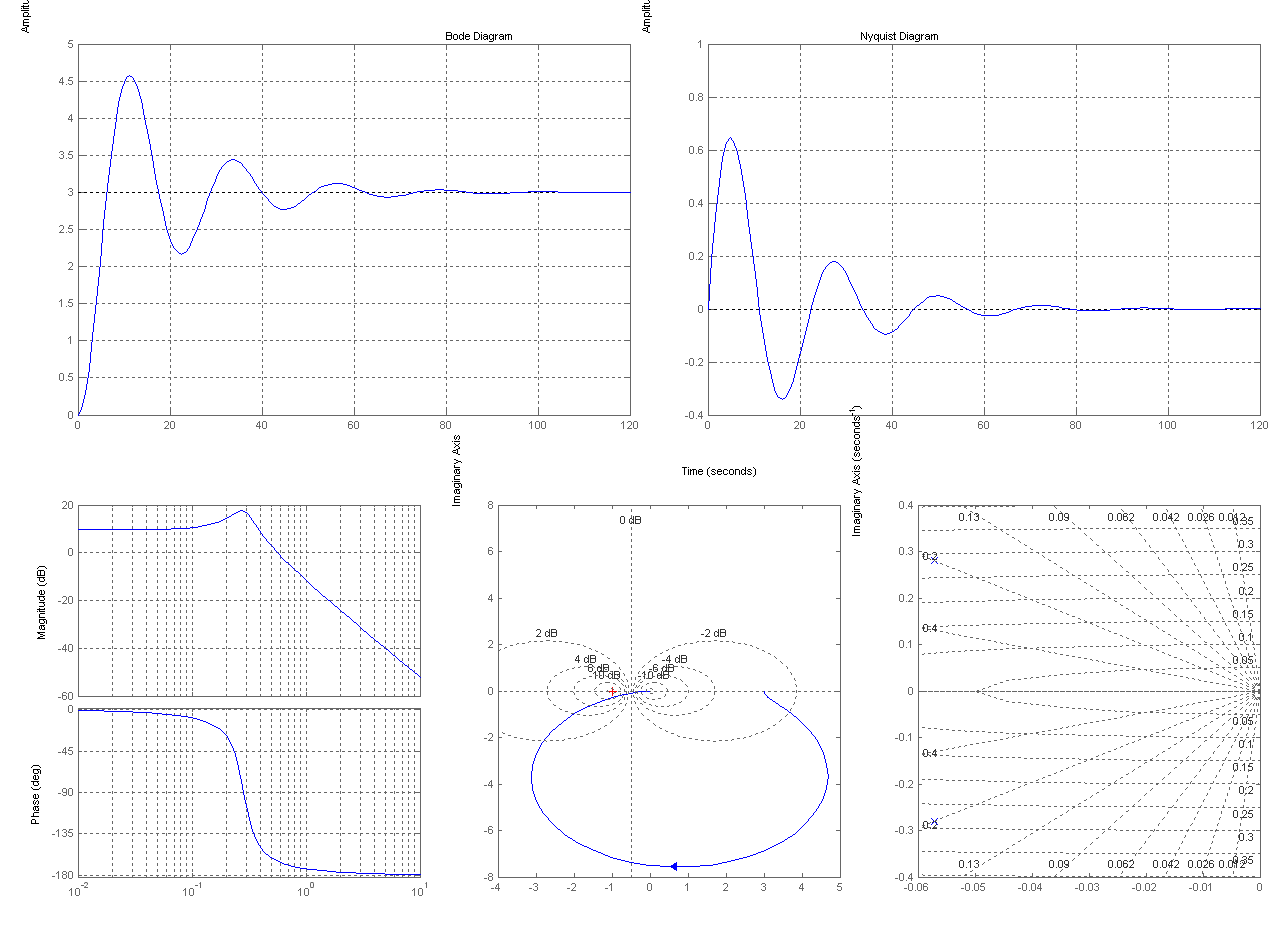
Колебательное звено 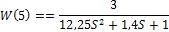    W(5)=tf([k], [T^2 2*T*xi 1])
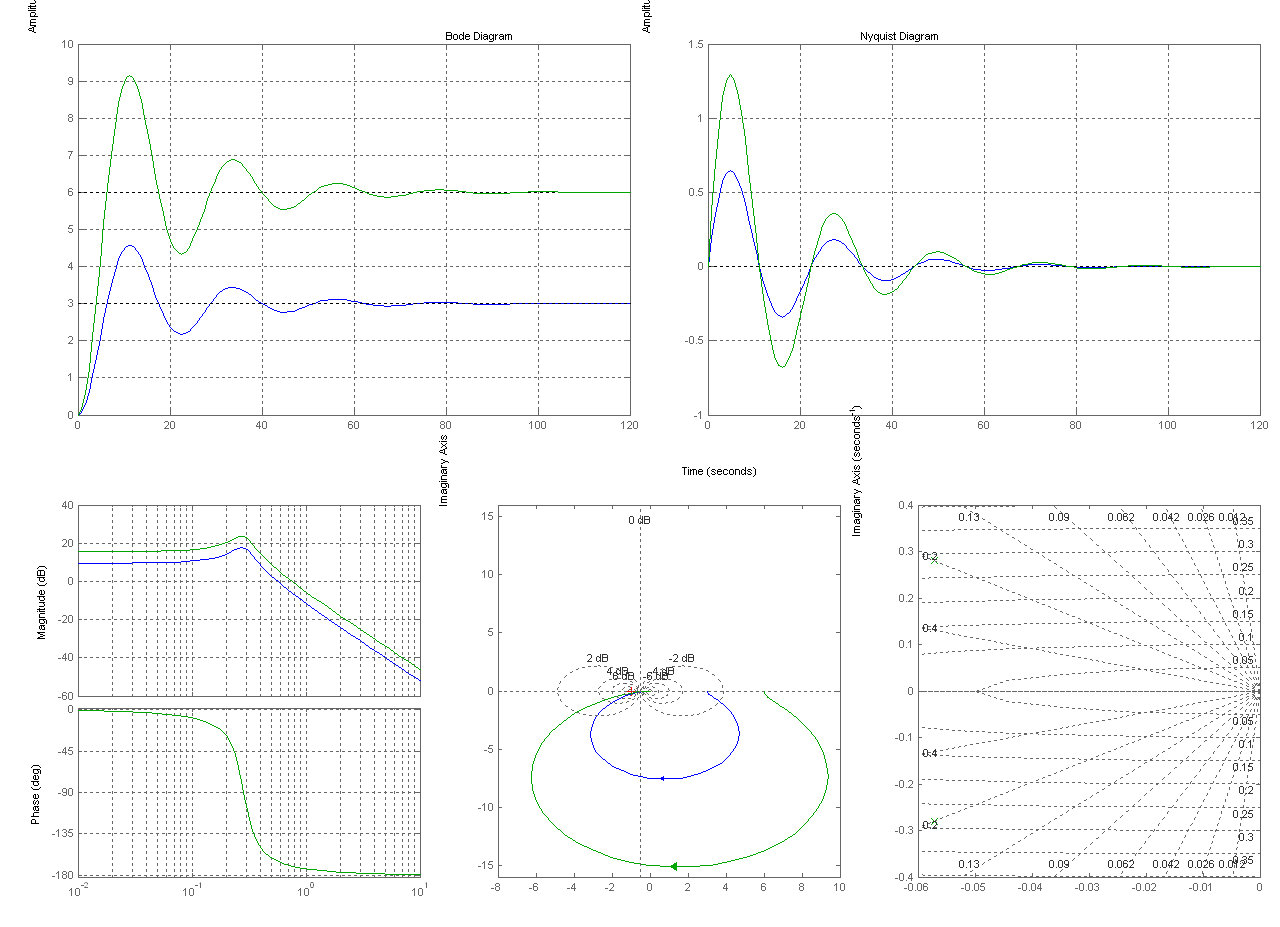
Сравнение характеристик колебательных звеньев а) и б) ζ1= 0,2– W(5) и ζ1= 0.2 – W(6) 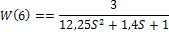    W(6)=tf([2*k], [T^2 2*T*xi 1])
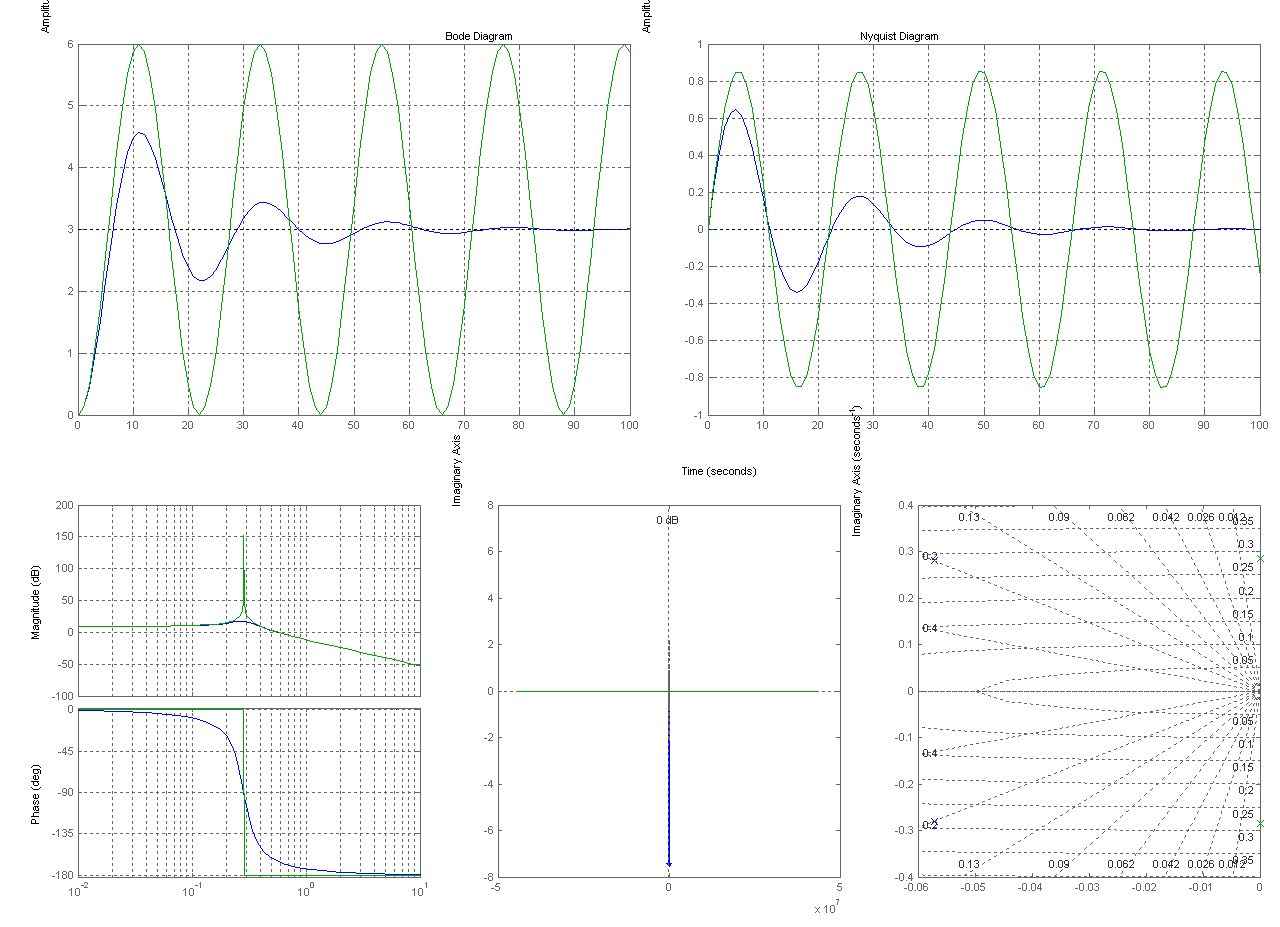
Сравнение характеристик колебательного звена а) и консервативного звена ζ1= 0,2– W(5) и ζ1= 0– W(7) 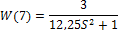      W(7)=tf([k], [T^2,2*T*0,1]);
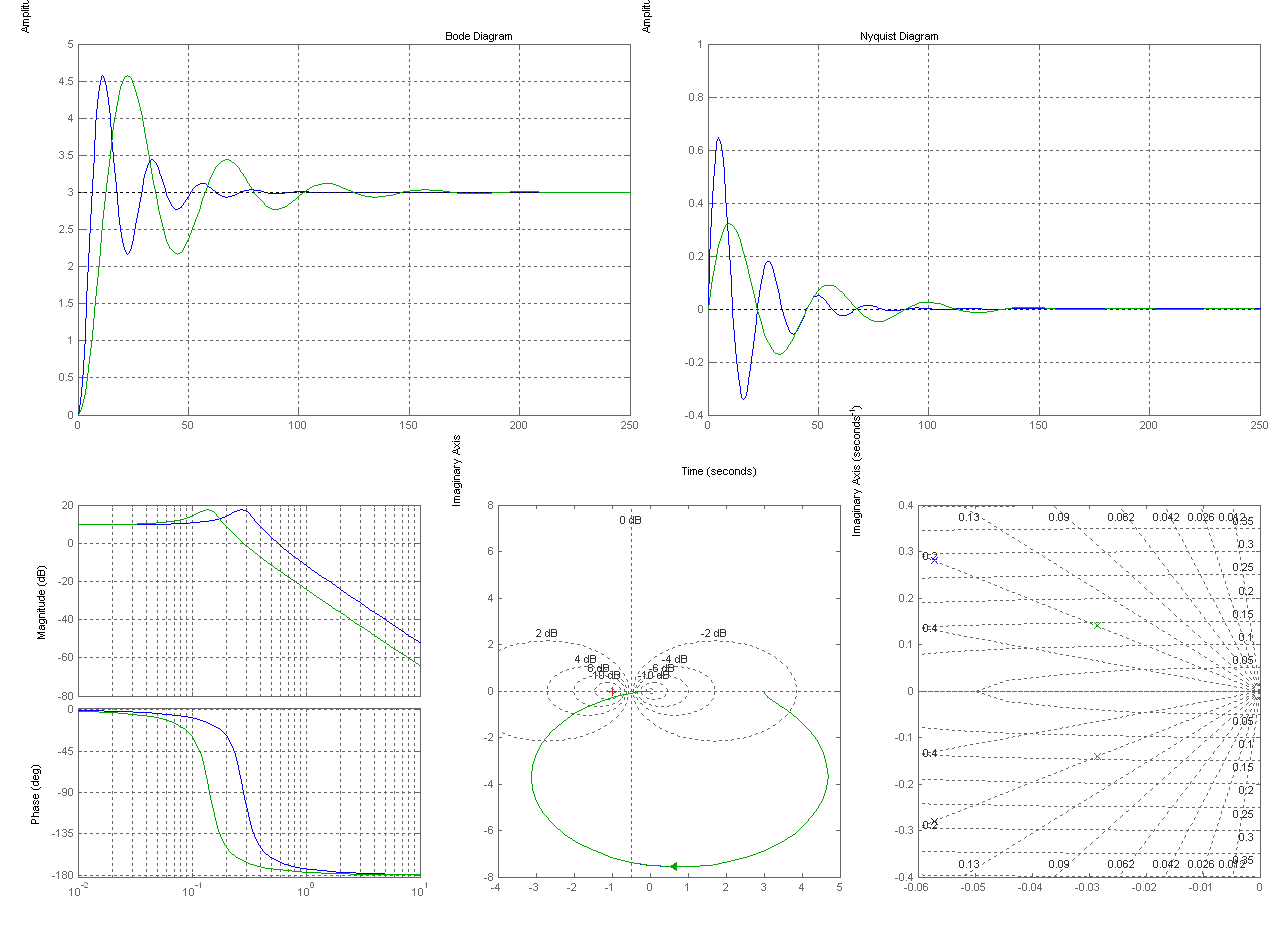
Сравнение характеристик колебательных звеньев а) и в) ζ1= 0,2– W(5) и ζ1= 0,2 – W(8) 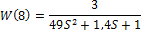  W7=tf([k],[(2*T)^2, 2*T*xi,1]);
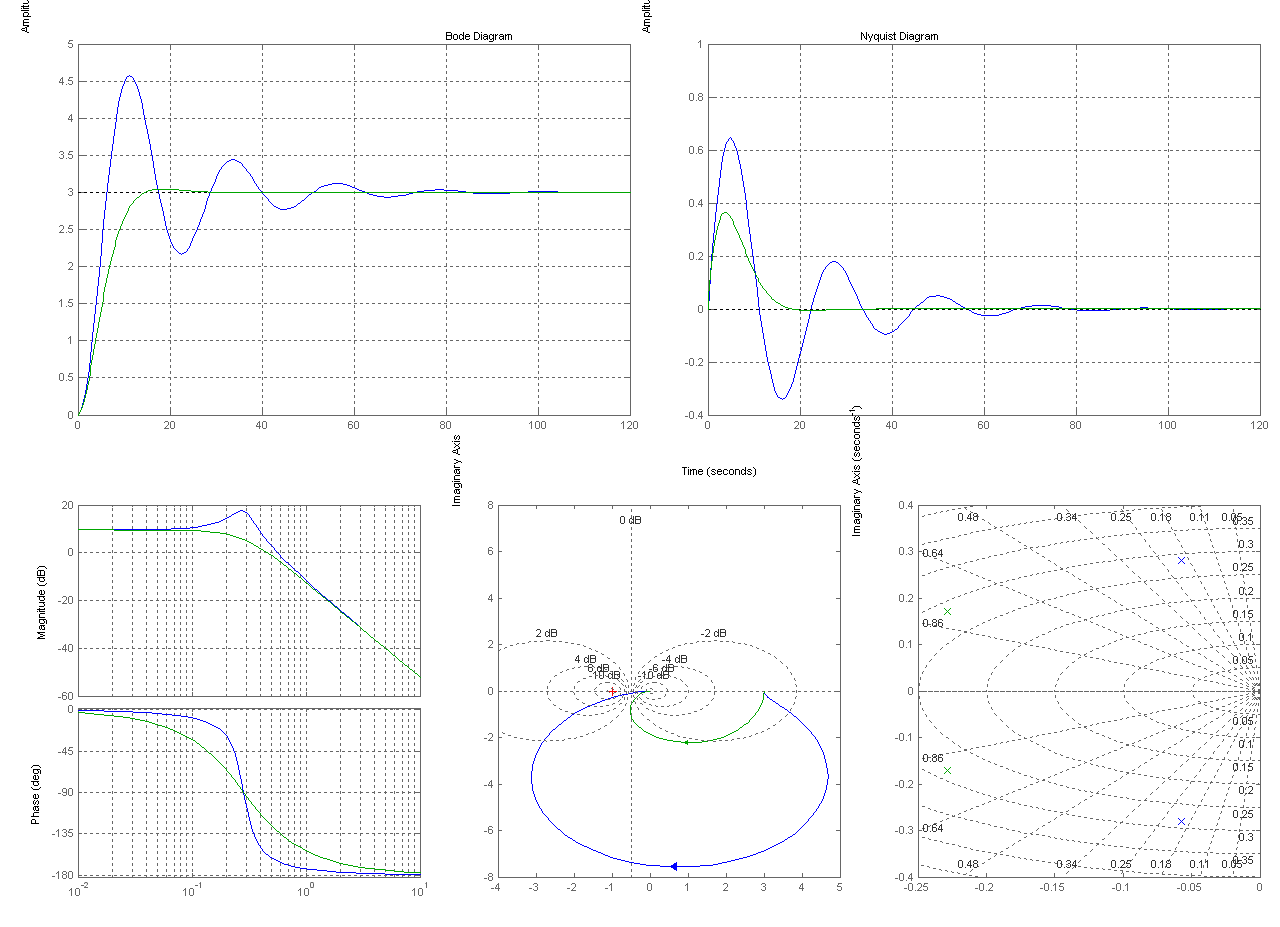
Сравнение характеристик колебательных звеньев а) и г) ζ1= 0,2– W(5) и ζ1= 0,8 – W(9) 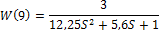  W(9)=tf([k], [T^2,2*T*0.8,1]);

Выводы:

Встроенные средства MATLAB позволяют моделировать динамические звенья, задавая их передаточные функции с помощью команды tf([ ], [ ]), и изучать их характеристики: переходный процесс (step( W)), импульсную переходную функцию (impulse( W)), амплитудно-фазовую характеристику (nyquist( W)), полюса (pole( W)) и нули (zero( W)). Построение графиков по передаточным функциям разных динамических звеньев на одной координатной плоскости позволяет сравнивать их характеристики между собой.

Изменение параметров передаточной функции исходного колебательного звена (W (5)) позволило выявить следующие зависимости:

· чем меньше коэффициент демпфирования ζ, тем меньше амплитуда колебаний переходного процесса и импульсной переходной функциии тем быстрее система переходит в установившийся режим;

· минимальное время переходного процесса достигается при ζ= 0 (консервативное звено);

· увеличение постоянной времени Tв 2 раза во столько же раз увеличивает период колебаний и уменьшает амплитуду колебаний импульсной переходной функции;

· увеличение коэффициента усиления K в 2 раза увеличивает амплитуду колебаний переходного процесса и импульсной переходной функции, усиливает установившийся сигнал во столько же раз и не влияет на период колебаний.