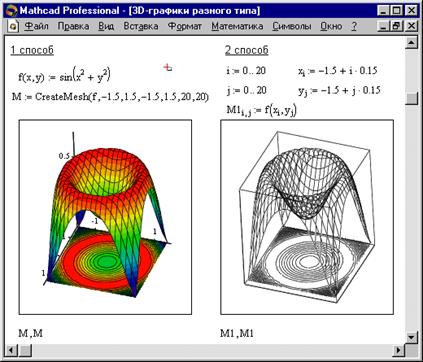
CreateMesh ( F (или G , или f 1, f 2, f 3), x 0, x 1, y 0, y 1, xgrid , ygrid , fmap )
Создает сетку на поверхности, определенной функцией F. x0, x1, y0, y1 – диапазон изменения переменных, xgrid , ygrid – размеры сетки переменных, fmap – функция отображения. Все параметры, за исключением F, - факультативные. Функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от –5 до 5 и с сеткой 20´20 точек.
|
Рисунок 2. Пример построения на одном рисунке двух 3D-графиков разного типа |
Пример использования функции CreateMesh для построения 3D-графиков приведен на Рисунке 2, способ 1. На Рисунке 2 построена одна и та же поверхность разными способами, с разным форматированием, причем изображены поверхности и под ними те же поверхности в виде контурного графика. Такое построение способно придать рисунку большую наглядность.
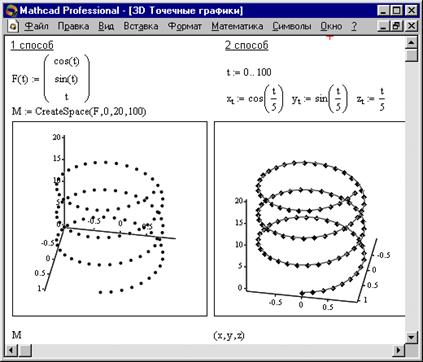
Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка Þ График Þ 3 D Точечный, причем поверхность задается параметрически – с помощью трех матриц (X , Y , Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1).
CreateSpace (F , t0, t1, tgrid, fmap)
Возвращает вложенный массив трех векторов, представляющих х-, у-, и z‑координаты пространственной кривой, определенной функцией F. t0 и t1 – диапазон изменения переменной, tgrid – размер сетки переменной, fmap – функция отображения. Все параметры, за исключением F, - факультативные.
Построение пересекающихся фигур
Особый интерес представляет собой возможность построения на одном графике ряда разных фигур или поверхностей с автоматическим учетом их взаимного пересечения. Для этого надо раздельно задать матрицы соответствующих поверхностей и после вывода шаблона 3D-графика перечислить эти матрицы под ним с использованием в качестве разделителя запятой.
|
|
Порядок выполнения работы
I. Построить график функции f(x) по точкам. Отрезок по оси X выбрать таким образом, чтобы было видно общее поведение функции (участки возрастания, убывания, минимумы, максимумы). Это замечание относиться также ко всем последующим задачам.
II. Построить быстрый график функции. Задать цвет линии черным, начертание – пунктир.
III. Построить графики функций в одной системе координат.
IV. Построить график функции, заданной параметрическими уравнениями.
V. Функция задана уравнением в полярной системе координат R=f(a). Построить график этой функции в полярной и прямоугольной системах координат.
VI. Построить график поверхности.(четыре вида: график поверхности, линий уровня, точечный и состоящий из столбцов). Изменить цвет поверхности сообразуясь со своим вкусом.
Варианты заданий
| № Вар. | Задание |
| 1. | I. 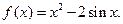 II.
II. 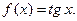 III.
III. 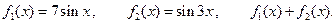 IV.
IV.  V.
V. 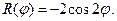 VI.
VI. 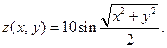
|
| 2. | I. 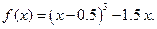 II.
II. 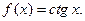 III.
III. 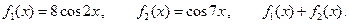 IV.
IV.  V.
V. 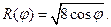 VI.
VI. 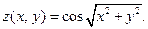
|
| 3. | I. 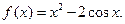 II.
II. 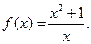 III.
III. 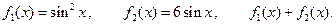 IV.
IV.  V.
V. 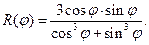 VI.
VI. 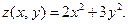
|
| 4. | I. 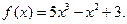 II.
II. 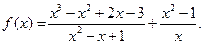 III.
III. 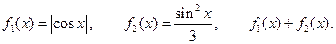 IV.
IV. 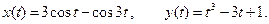 V.
V. 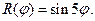 VI.
VI. 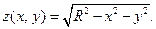
|
| 5. | I. 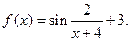 II.
II. 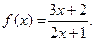 III.
III. 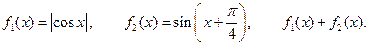 IV.
IV. 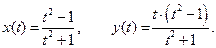 V.
V. 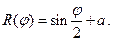 VI.
VI. 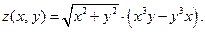
|
| 6. | I. 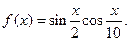 II.
II. 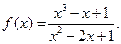 III.
III. 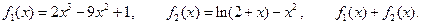 IV.
IV. 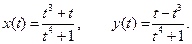 V.
V. 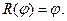 VI.
VI. 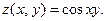
|
| 7. | I. 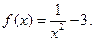 II.
II. 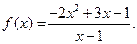 III.
III. 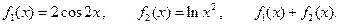 IV.
IV. 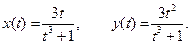 V.
V. 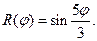 VI.
VI. 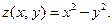
|
| 8. | I. 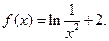 II.
II. 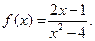 III.
III. 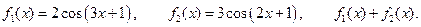 IV.
IV.  V.
V. 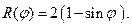 VI.
VI. 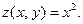
|
| 9. | I. 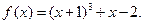 II.
II. 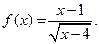 III.
III. 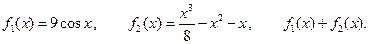 IV.
IV.  V.
V. 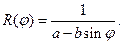 VI.
VI. 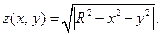
|
| 10. | I. 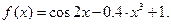 II.
II. 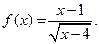 III.
III. 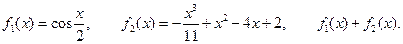 IV.
IV.  V.
V. 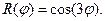 VI.
VI. 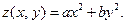
|
Контрольные вопросы
1. Типы графиков в системе Mathcad.
2. Способы вставки графика функции в декартовых координатах.
3. Отличие быстрого графика от графика по точкам.
4. Опишите последовательность действий для построения графика функции y = sin x на интервале [0; 7].
5. Размещение нескольких функций на одном графике.
6. Каков интервал изменения аргумента для "быстрого графика"?
7. Что будет, если функция, график которой строится как "быстрый", определена только на неотрицательных значениях?
8. Как изменить диапазон аргумента на графике?
9. Средства исследования графика в декартовых координатах.
10. Возможности настройки графика в декартовых координатах.
11. График в полярных координатах.
12. Способ редактирования полярного графика;
13. Действия для построения графика линий уровня по точкам.
14. Построение объемной кривой.
15. Действия для построения быстрого графика - поверхности.
16. Возможности настройки объемного графика.
17. Как создать контурный график;
18. Что из себя представляет точечный график;