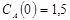Основы работы с Mathcad
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Северо-Кавказский горно-металлургический институт
(государственный технологический университет)
Кафедра теории и автоматизации металлургических процессов и печей
Методические указания к лабораторным работам по курсу
«МОДЕЛИРОВАНИЕ СИСТЕМ И ПРОЦЕССОВ»
Владикавказ 2013
Лабораторная работа 1.
Основы работы с Mathcad
Цель работы: ознакомиться с базовыми принципами работы Mathcad
Теоретические положения
К основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры.
Операторы - элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.
Оператор определяет: действие, которое должно выполняться при наличии тех или иных значений операндов; сколько, где и какие операнды должны быть введены в оператор.
Операнд - число или выражение, на которое действует оператор. После указания операндов операторы становятся исполняемыми по документу блоками.
К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа.
Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.
В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения (см. Приложение 1).
Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Оptions команды Математика Опции.
Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной.
Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши : (двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью знака  (клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание (см. Пример 1 Рисунка 1).
(клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание (см. Пример 1 Рисунка 1).

MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания (  ), а при втором - производятся действия, предписанные локальным оператором присваивания (:=), и отображаются все необходимые результаты вычислений (=).
), а при втором - производятся действия, предписанные локальным оператором присваивания (:=), и отображаются все необходимые результаты вычислений (=).
Существуют также жирный знак равенства = (комбинация клавиш Ctrl + =), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства ® (комбинация клавиш Ctrl + .).
Дискретные аргументы - особый класс переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является).
Эти переменные имеют ряд фиксированных значений, либо целочисленных (1 способ), либо в виде чисел с определенным шагом, меняющихся от начального значения до конечного (2 способ).
1. Name := Nbegin .. Nend,
где Name - имя переменной, Nbegin - ее начальное значение, Nend - конечное значение, .. - символ, указывающий на изменение переменной в заданных пределах (вводится клавишей ;). Если Nbegin < Nend, то шаг переменной будет равен +1, иначе -1.
2. Name := Nbegin, (Nbegin + Step) .. Nend
Здесь Step - заданный шаг изменения переменной (он должен быть положительным, если Nbegin < Nend, или отрицательным в обратном случае).
Дискретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы (Пример 3 Рисунка 1).
Массив - имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов:
· одномерные (векторы);
· двумерные (матрицы).
Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии со значением системной переменной ORIGIN .
Векторы и матрицы можно задавать различными способами:
· с помощью команды Вставка Матрица, или комбинации клавиш Ctrl + M, или щелчком на кнопке  панели Матрица,заполнив массив пустых полей для не слишком больших массивов;
панели Матрица,заполнив массив пустых полей для не слишком больших массивов;
· с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов через их индексы (Пример 3 Рисунка 1).
Функция - выражение, согласно которому проводятся некоторые вычисления с аргументами и определяется его числовое значение.
Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции (см. Пример 2 Рисунка 1).
Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.
Функции в пакете MathCAD могут быть встроенные (см. Приложение 3), т. е. заблаговременно введенные разработчиками, и определенные пользователем. Способы вставки встроенной функции:
1. Выбрать пункт меню Вставка Функция.
2. Нажать комбинацию клавиш Ctrl + E.
3. Щелкнуть на кнопке 
Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов:
· текстовая область предназначена для небольших кусков текста - подписей, комментариев и т. п. Вставляется с помощью команды Вставка Ю Текстовая регион или комбинации клавиш Shift + " (двойная кавычка);
· текстовый абзац применяется в том случае, если необходимо работать с абзацами или страницами. Вставляется с помощью комбинации клавиш Shift + Enter.
Графические области
Графические области делятся на три основных типа - двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на основании обработанных данных.
Для создания декартового графика:
1. Установить визир в пустом месте рабочего документа.
2. Выбрать команду Вставка Ю График Ю Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку  панели Графики. Появится шаблон декартового графика.
панели Графики. Появится шаблон декартового графика.
3. Введите в средней метке под осью Х первую независимую переменную, через запятую - вторую и так до 10, например х1, х2, …
4. Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую - вторую и т. д., например у1(х1), у2(х2), …, или соответствующие выражения.
5. Щелкните за пределами области графика, что бы начать его построение.
Трехмерные, или 3D-графики, отображают функции двух переменных вида Z(X, Y). При построении трехмерных графиков в ранних версиях MathCAD поверхность нужно было определить математически (Рисунок 2, способ 2). Теперь применяют функцию MathCADCreateMesh.
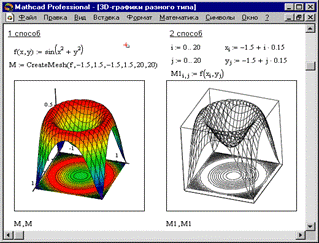
Рисунок 2.
CreateMesh(F (или G,или f1, f2, f3), x0, x1, y0, y1, xgrid, ygrid, fmap)Создает сетку на поверхности, определенной функцией F. x0, x1, y0, y1 - диапазон изменения переменных, xgrid, ygrid - размеры сетки переменных, fmap - функция отображения. Все параметры, за исключением F, - факультативные. Функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от -5 до 5 и с сеткой 20*20 точек.
Пример использования функции CreateMesh для построения 3D-графиков приведен на Рисунке 2, способ 1. На Рисунке 2 построена одна и та же поверхность разными способами, с разным форматированием, причем изображены поверхности и под ними те же поверхности в виде контурного графика. Такое построение способно придать рисунку большую наглядность.
Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка График Ю 3D Точечный, причем поверхность задается параметрически - с помощью трех матриц (X, Y, Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1).
CreateSpace (F , t0, t1, tgrid, fmap)
Возвращает вложенный массив трех векторов, представляющих х-, у-, и z-координаты пространственной кривой, определенной функцией F. t0 и t1 - диапазон изменения переменной, tgrid - размер сетки переменной, fmap - функция отображения. Все параметры, за исключением F, - факультативные.
Особый интерес представляет собой возможность построения на одном графике ряда разных фигур или поверхностей с автоматическим учетом их взаимного пересечения. Для этого надо раздельно задать матрицы соответствующих поверхностей и после вывода шаблона 3D-графика перечислить эти матрицы под ним с использованием в качестве разделителя запятой (Рисунок 4).
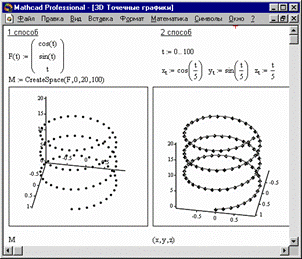
Рисунок 3.
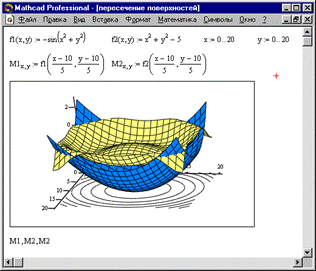
Рисунок 4.
Лабораторная работа №2
МОДЕЛИРОВАНИЕ КИНЕТИКИ ХИМИЧЕСКИХ РЕАКЦИЙ
Цель работы: получение навыков построения математических моделей необратимых химических реакций
1. Теоретические положения
Реакция называется простой, если скорость образования (расходования) вещества С i зависит от концентраций только исходных веществ. Принятые или истинные механизмы простых реакций учитывают только один путь химического превращения.
Если в простой реакции участвует n веществ 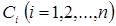 , то материальный баланс реакции выражается уравнением:
, то материальный баланс реакции выражается уравнением:
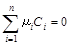 , (1.1)
, (1.1)
где 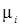 - стехиометрические коэффициенты (отрицательные для исходных и положительные для образующихся веществ).
- стехиометрические коэффициенты (отрицательные для исходных и положительные для образующихся веществ).
Коэффициент 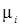 показывает, сколько молекул вещества С i участвует в реакции. Изменение концентрации вещества
показывает, сколько молекул вещества С i участвует в реакции. Изменение концентрации вещества 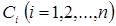 в простой реакции описывается дифференциальным уравнением:
в простой реакции описывается дифференциальным уравнением:
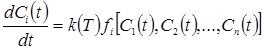 . (1.2)
. (1.2)
Функция 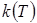 называется константой скорости реакции и чаще всего задается уравнением Аррениуса:
называется константой скорости реакции и чаще всего задается уравнением Аррениуса:
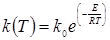 , (1.3)
, (1.3)
где 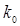 - предэкпоненциальный множитель, характеризующий вероятность взаимодействия молекул веществ, энергия которых достаточна для осуществления реакции; Е – энергия активации, равная избытку энергии относительно средней энергии молекул при данной температуре, которым должны обладать молекулы веществ для осуществления химического взаимодействия; R - универсальная газовая постоянная; Т – абсолютная температура.
- предэкпоненциальный множитель, характеризующий вероятность взаимодействия молекул веществ, энергия которых достаточна для осуществления реакции; Е – энергия активации, равная избытку энергии относительно средней энергии молекул при данной температуре, которым должны обладать молекулы веществ для осуществления химического взаимодействия; R - универсальная газовая постоянная; Т – абсолютная температура.
Функция fi в уравнении (1.2) обычно имеет следующий вид:
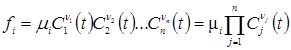 , (1.4)
, (1.4)
где 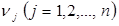 - постоянные положительные величины, называемые порядками реакции по веществам
- постоянные положительные величины, называемые порядками реакции по веществам 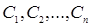 .
.
Стехиометрическое уравнение реакции (1.1) показывает, в каких соотношениях компоненты участвуют в химической реакции. Это уравнение связывает исходные реагенты, конечные продукты и представляет собой уравнение материального баланса реакции в целом или ее отдельных стадий. Если в результате химического взаимодействия а моль вещества А и b моль вещества В образуется с моль вещества С, стехиометрическое уравнение реакции представляется в виде:
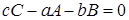 , (1.5)
, (1.5)
где a, b, c – стехиометрические коэффициенты.
Механизм химической реакции раскрывает все элементарные стадии превращения исходных компонентов в конечные продукты через промежуточные вещества. Предположим, что механизм реакции (1.5) включает три стадии:
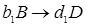 , (1.6)
, (1.6)
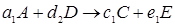 , (1.7)
, (1.7)
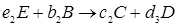 . (1.8)
. (1.8)
Здесь А и В – исходные вещества, С- конечный продукт реакции, D – промежуточный продукт. Каждая стадия реакции описывается стехиометрическим уравнением:
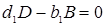 , (1.9)
, (1.9)
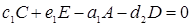 , (1.10)
, (1.10)
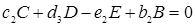 . (1.11)
. (1.11)
Реакцию в целом механизма описанного уравнениями (1.6)-(1.8) получают путем суммирования уравнений
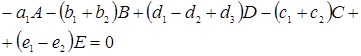 (1.12)
(1.12)
Уравнение (1.12) тождественно уравнению (1.5), если выполняются следующие условия:
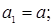
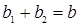 ;
; 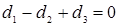 ;
; 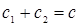 ;
; 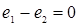 .
.
Скорость химической реакции 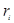 выражается числом
выражается числом 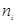 молей компонента, которое образуется или расходуется в единицу времени в единице объема V. Кинетические уравнения реакции имеет вид:
молей компонента, которое образуется или расходуется в единицу времени в единице объема V. Кинетические уравнения реакции имеет вид:
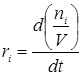 . (1.13)
. (1.13)
Отношение числа молей i-го компонента к объему реакционной массы V представляет собой концентрацию этого компонента:
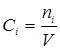 . (1.14)
. (1.14)
При постоянном объеме реагентов скорость реакции можно выразить через концентрацию:
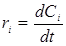 . (1.15)
. (1.15)
Скорость реакции типа 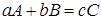 при постоянной температуре выражается уравнением:
при постоянной температуре выражается уравнением:
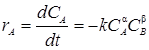 , (1.16)
, (1.16)
где a и b - определяют порядок реакции, k – константа скорости химических реакций.
Механизм реакции называют истинным, если каждая стадия описывается кинетическим уравнением, составленным в соответствии со стехиометрическим уравнением этой стадии. Приближенный механизм реакции может хорошо аппроксимировать опытные данные по кинетике, но при этом кинетические уравнения скорости не соответствуют стехиометрическим уравнениям. При истинном механизме реакции сумма стехиометрических коэффициентов исходных компонентов равна порядку реакции, а порядок реакции по отдельному компоненту равен стехиометрическому коэффициенту этого компонента.
Например, для реакции типа 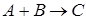 стехиометрическое уравнение записывается в виде (1.5). Кинетическое уравнение скорости для продукта реакции выражается уравнением:
стехиометрическое уравнение записывается в виде (1.5). Кинетическое уравнение скорости для продукта реакции выражается уравнением:
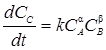 . (1.17)
. (1.17)
2. Содержание работы
В данной лабораторной работе необходимо в соответствии с уравнениями химический кинетики построить математические модели реакций нескольких типов.
Задача 1
Построить математическую модель простой необратимой реакции первого порядка 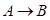 . Известны начальные концентрации веществ
. Известны начальные концентрации веществ 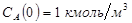 и
и 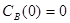 ; константа скорости химической реакции при температуре Т1 :
; константа скорости химической реакции при температуре Т1 : 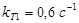 . Требуется найти кинетические зависимости компонентов реакции в виде функций
. Требуется найти кинетические зависимости компонентов реакции в виде функций 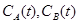 .
.
Решение
Кинетические уравнения имеют вид:
- для компонента А: 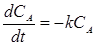 ;
;
- для компонента В: 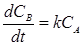 .
.
Уравнения (19) и (20) представляют собой систему линейных дифференциальных уравнений. Максимальные значения концентраций СА и СВ определяются начальной концентрацией реагента А. Рассматриваемая реакция идет до конца, поэтому конечная концентрация продукта В будет численно равна начальной концентрации исходного вещества А:
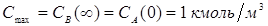 .
.
Полученная система дифференциальных уравнений решается в системе MathCad с помощью встроенной функции rkfixed, реализующей численный метод Рунге-Кутта.
Программа решения в среде MathCad
1. Задаем значение константы скорости реакции 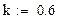
|
2. Задаем векторную функцию двух аргументов 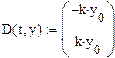
|
3. Задаем вектор начальных условий 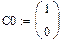
|
4. Задаем число шагов, на которых численно находится решение 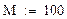
|
5. Для решения системы уравнений используем встроенную функцию, реализующую метод Рунге-Кутта с фиксированным шагом
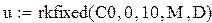
|
6. Строим графики искомых функций:
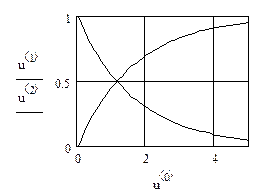
|
Задача 2
Построить модель двухстадийной последовательной химической реакции 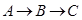 , если известны: начальные концентрации веществ
, если известны: начальные концентрации веществ 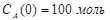 ;
; 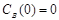 ;
; 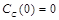 и относительные константы скорости:
и относительные константы скорости: 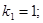
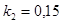 .
.
Решение
Кинетические уравнения имеют вид:
- для компонента А 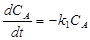 ;
;
-для компонента В 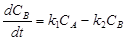 ;
;
- для компонента С 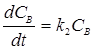 .
.
Программа решения среде MathCad
| 1. Значения констант скоростей реакций | |
| 2. Вектор-функция | |
| 3. Вектор начальных условий | 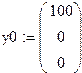
|
| 4. Число точек для поиска решения | М:=100 |
| 5. Функция для решения системы | 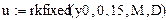
|
|
| |
Задача 3
Составить математическую модель обратимой химической реакции первого порядка вида 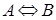 , если известны начальные концентрации
, если известны начальные концентрации 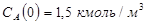 ,
, 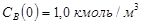 ; начальные скорости реакции
; начальные скорости реакции 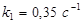 ;
; 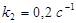 .
.
Решение:
Кинетические уравнения имеют вид:
- для компонента А
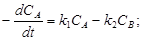
- для компонента В
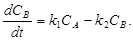
Программа решения среде MathCad
| 1. Значения констант скоростей реакций | 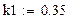
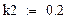
|
| 2. Вектор-функция | 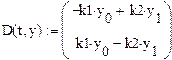
|
| 3. Вектор начальных условий | М:=100 |
| 4. Число точек для поиска решения | 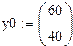
|
| 5. Функция для решения системы | 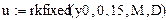
|
|
| |
3. Порядок выполнения работы
1. В соответствии с вариантом задания построить кинетическую модель необратимой реакции первого порядка 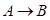 , решить математическую модель в системе MathCAD и построить графики кинетических кривых, полученных на модели.
, решить математическую модель в системе MathCAD и построить графики кинетических кривых, полученных на модели.
2. Построить модель двухстадийной последовательной химической реакции 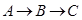 , решить модель в системе MathCAD и построить графики кинетических кривых, полученных на модели.
, решить модель в системе MathCAD и построить графики кинетических кривых, полученных на модели.
3. Составить модель обратимой химической реакции первого порядка вида 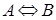 , решить математическую модель в системе MathCAD и построить графики кинетических кривых, полученных на модели.
, решить математическую модель в системе MathCAD и построить графики кинетических кривых, полученных на модели.
4. Исходными данными являются значения концентраций веществ, участвующих в реакциях, и констант скоростей реакций, численные значения которых представлены ниже.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Содержание отчета
4.1. Тема и цель работы, номер варианта
4.2. Постановка задачи
4.3. Математические модели реакций и графики кинетических зависимостей
4.4. Выводы
5. Контрольные вопросы
5.1. Какая химическая реакция называется простой?
5.2. Что представляет собой константа скорости реакции, от каких параметров она зависит?
5.3. Что показывают стехиометрические коэффициенты?
5.4. Какой механизм реакции называется истинным?
Лабораторная работа №3
Применение численных методов для решения простейших задач теплообмена
Цель работы: изучить метод Ньютона для решения нелинейных уравнений и использовать его при решении задачи радиационного теплообмена.
1. Теоретические положения
1.1. Постановка задачи
Пусть требуется рассчитать температуру нагревателя 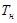 электрической печи сопротивления.
электрической печи сопротивления.
Считаем заданными:
- температуру поверхности нагреваемого металла 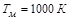 ;
;
- степень черноты поверхности нагреваемого металла 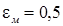
- полезную удельную мощность нагревателя 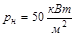 ;
;
- зависимость степени черноты нагревателя от температуры 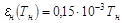 (в интервале 1000-2000 К).
(в интервале 1000-2000 К).
Для решения данной задачи запишем уравнение теплового баланса нагревателя:
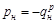 , (4.1)
, (4.1)
где 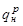 - плотность потока результирующего излучения на его поверхности.
- плотность потока результирующего излучения на его поверхности.
Выразим 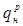 через неизвестную температуру
через неизвестную температуру 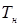 , рассматривая поверхности нагревателя и металла как бесконечные параллельные плоскости:
, рассматривая поверхности нагревателя и металла как бесконечные параллельные плоскости:
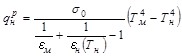 , (4.2)
, (4.2)
где 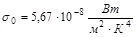 - постоянная Стефана - Больцмана.
- постоянная Стефана - Больцмана.
Подставив выражение (3.2) в уравнение теплового баланса (3.1), получим:
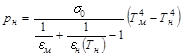 . (4.3)
. (4.3)
Зависимость (3.3) представляет собой нелинейное уравнение относительно искомой температуры 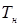 . Для решения поставленной задачи рассмотрим применение метода Ньютона (метода касательных).
. Для решения поставленной задачи рассмотрим применение метода Ньютона (метода касательных).
Метод Ньютона (метод касательных)
Данный метод предназначен для решения нелинейных уравнений вида: 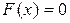 , (4.4)
, (4.4)
где функция 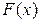 определена и непрерывна на конечном или бесконечном интервале
определена и непрерывна на конечном или бесконечном интервале 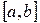 . Всякое число
. Всякое число 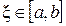 , обращающее функцию
, обращающее функцию 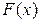 в нуль, называется корнем уравнения
в нуль, называется корнем уравнения 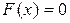 . Пусть корень уравнения
. Пусть корень уравнения 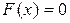 отделен на отрезке [a , b], причем
отделен на отрезке [a , b], причем 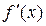 и
и 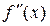 непрерывны и сохраняют определенные знаки при
непрерывны и сохраняют определенные знаки при 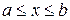 . Если на некотором произвольном шаге n найдено приближенное значение корня
. Если на некотором произвольном шаге n найдено приближенное значение корня 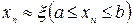 , то можно уточнить это значение по методу Ньютона. Положим
, то можно уточнить это значение по методу Ньютона. Положим
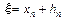 , (4.5)
, (4.5)
где 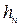 - малая величина.
- малая величина.
Применяя формулу Тейлора, получим:
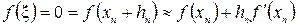 .
.
Следовательно,
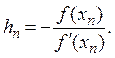
Внеся эту поправку в формулу (3.1), найдем следующее (по порядку) приближение корня:
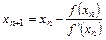 ,
, 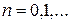 (4.6)
(4.6)
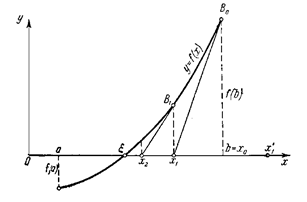
Геометрически метод Ньютона эквивалентен замене дуги кривой 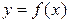 касательной, проведенной в некоторой точке кривой (рис. ). Положим для определенности, что
касательной, проведенной в некоторой точке кривой (рис. ). Положим для определенности, что 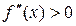 при
при 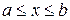 и
и 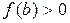 . Выберем,
. Выберем, 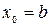 , для которого
, для которого 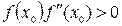 . Проведем касательную к кривой
. Проведем касательную к кривой 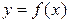 в точке B0 с координатами
в точке B0 с координатами 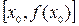 . В качестве первого приближения
. В качестве первого приближения 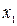 корня возьмем абсциссу точки пересечения касательной с осью Ox.
корня возьмем абсциссу точки пересечения касательной с осью Ox.
|
Рисунок |
Рис. Геометрическая интерпретация метода Ньютона
Через точку 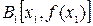 снова проведем касательную, абсцисса точки пересечения которой даст второе приближение
снова проведем касательную, абсцисса точки пересечения которой даст второе приближение 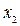 корня и т.д. Формулу для уточнения корня можно получить из треугольника
корня и т.д. Формулу для уточнения корня можно получить из треугольника 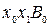 , образованного касательной, проведенной в точке B0, осью абсцисс и перпендикуляром, восстановленным из точки
, образованного касательной, проведенной в точке B0, осью абсцисс и перпендикуляром, восстановленным из точки 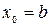 . Тогда
. Тогда 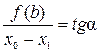 . Так как угол a образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е.
. Так как угол a образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е. 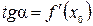 и
и 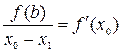 . Тогда справедливо, что
. Тогда справедливо, что
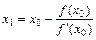 (4.7)
(4.7)
или для любого шага n
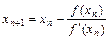 . (4.8)
. (4.8)
В качестве начальной точки 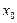 можно принять либо один из концов отрезка [a , b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие
можно принять либо один из концов отрезка [a , b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие
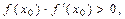
т.е. функция и ее вторая производная в точке 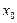 должны быть одного знака.
должны быть одного знака.
При использовании метода Ньютона исходное уравнение необходимо привести к виду:
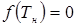 . (4.9)
. (4.9)
Тогда в левой части уравнения (4.3) окажется функция:
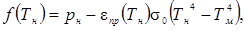 (4.10)
(4.10)
где 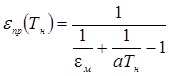 - приведенная степень черноты рассматриваемой системы.
- приведенная степень черноты рассматриваемой системы.
Значение уравнения (4.10) при текущем значении 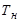 называют невязкой уравнения (4.9). На каждом шаге итераций последующему приближению искомой величины соответствует точка пересечения с остью абсцисс касательной к кривой
называют невязкой уравнения (4.9). На каждом шаге итераций последующему приближению искомой величины соответствует точка пересечения с остью абсцисс касательной к кривой 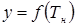 в точке предыдущего приближения. С учетом того, что тангенс угла наклона касательной численно равен производной от невязки исследуемой функции:
в точке предыдущего приближения. С учетом того, что тангенс угла наклона касательной численно равен производной от невязки исследуемой функции: 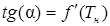 , получим следующее выражение для
, получим следующее выражение для 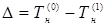 :
:
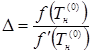 , (4.11)
, (4.11)
т. е. последующее приближение может быть найдено по формуле:
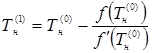 . (4.12)
. (4.12)
В общем случае итерационная формула для метода Ньютона имеет вид:
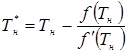 . (4.13)
. (4.13)
В процессе расчета по этой формуле значения искомой температуры нагревателя быстро приближаются к решению исходного уравнения, при этом значения невязок стремятся к нулю. Рассмотрим особенности применения метода Ньютона для решения рассматриваемой задачи теплообмена. Отметим, что рассчитывать производную 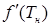 можно достаточно приближено, т. к. ее величина определяет лишь значение очередного приближения, не влияя на окончательный результат расчета. Пренебрегая зависимостью
можно достаточно приближено, т. к. ее величина определяет лишь значение очередного приближения, не влияя на окончательный результат расчета. Пренебрегая зависимостью 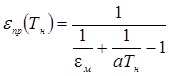 при дифференцировании невязки, получим выражение для приближенного значения производной:
при дифференцировании невязки, получим выражение для приближенного значения производной:
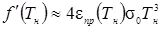 (4.14)
(4.14)
и итерационная формула примет вид:
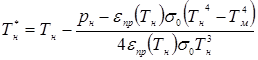 . (4.15)
. (4.15)
Решение поставленной задачи реализовано в вычислительной среде MathCAD. Расчет по формуле (3.15) приводит к значению искомой величины: 1544,3. Программа, реализующая алгоритм метода Ньютона в системе MathCAD, представлена ниже.
| Программа |
| 1. Задаем исходные данные: |
Температура поверхности металла: 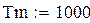
|
Степень черноты поверхности нагреваемого металла: 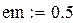
|
Полезная удельная мощность нагревателя: 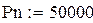
|
Зависимость степени черноты нагревателя от температуры 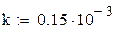
|
| Отделяем корни уравнения: |
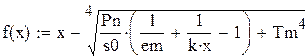
|
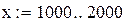
|
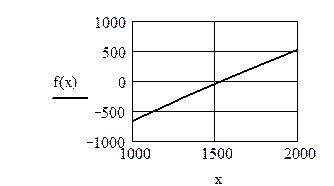
|
| 2. Определяем неподвижную точку: |
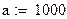 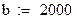
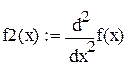
|
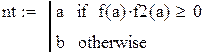
|
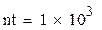
|
| 3. Вычисляем значения итерационной последовательности с использованием рекуррентной формулы метода касательных: |
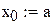 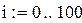
|
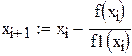
|
 
|
| 4. Создаем функцию, реализующую метод касательных |
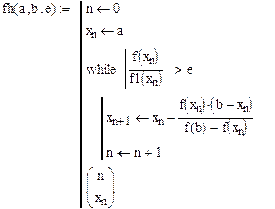
|
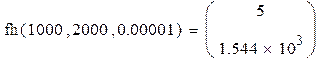
|
| 5. Проверяем полученные результаты |
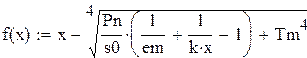
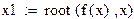
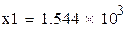
|
4. Задание для выполнения
| Вар. №1 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1100 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,5 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 55 |
| 4. | Зависимость степени черноты нагревателя от температуры, | 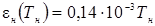
|
| Вар. №2 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1200 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,55 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 60 |
| 4. | Зависимость степени черноты нагревателя от температуры, | 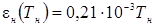
|
| Вар. №3 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1300 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,6 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 65 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 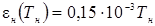
|
| Вар. №4 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1400 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,65 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 70 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 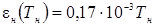
|
| Вар. №5 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1500 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,7 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 75 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 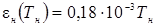
|
| Вар. №6 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1600 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,75 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 80 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 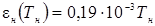
|
| Вар. №7 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1700 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,8 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 85 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 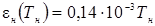
|
| Вар. №8 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 1800 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,85 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 90 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 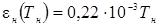
|
| Вар. №9 | ||
| Температура поверхности нагреваемого металла (Тм), К | 1900 | |
| Степень черноты поверхности нагреваемого металла, em | 0,9 | |
| Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 95 | |
| Зависимость степени черноты нагревателя от температуры, en | 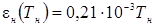
| |
| Вар. №10 | ||
| 1. | Температура поверхности нагреваемого металла (Тм), К | 2000 |
| 2. | Степень черноты поверхности нагреваемого металла, em | 0,95 |
| 3. | Полезная удельная мощность нагревателя, кВт/ м2 (рn) | 100 |
| 4. | Зависимость степени черноты нагревателя от температуры, en | 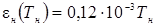
|
5. Контрольные вопросы
- Какой физический смысл имеет уравнение, используемое для получения решения?
- Что является причиной нелинейности уравнения?
- В чем состоит идея метода Ньютона?
- Какие существуют еще методы для численного решения нелинейных уравнений?
Лабораторная работа №4
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ВЫЩЕЛАЧИВАНИЯ
ЦИНКОВЫХ ОГАРКОВ
Цель работы: построить математическую модель каскада реакторов процесса выщелачивания цинковых огарков и провести с ее помощью исследование процесса.
1. Теоретические положения
Основная цель выщелачивания цинкового огарка – возможно более полное извлечение в раствор цинка и сопутствующих ему ценных компонентов при минимальном загрязнении примесями, вредными для последующих операций. Взаимодействие компонентов огарка и отработанного электролита осуществляется по реакции:
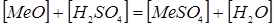 (5.1)
(5.1)
Реакции растворения необратимы, так как не зависят от концентрации продуктов реакции. Твердые и газообразные продукты реакции и исходные вещества могут влиять только экранированием растворяющейся фазы. Температура и гидродинамические параметры выщелачивания определяют скорость растворения кинетическими и диффузионными факторами. Скорость выщелачивания может быть описана уравнениями химической кинетики:
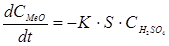 , (5.2)
, (5.2)
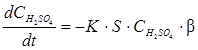 , (5.3)
, (5.3)
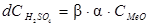 , (5.4)
, (5.4)
где 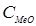 - концентрация оксидов металлов;
- концентрация оксидов металлов; 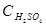 - концентрация серной кислоты; S – поверхность твердой фазы; b - стехиометрический коэффициент, определяющий расход реагента (в молях) на один моль сырья.
- концентрация серной кислоты; S – поверхность твердой фазы; b - стехиометрический коэффициент, определяющий расход реагента (в молях) на один моль сырья.
Для гетерогенного процесса, описываемого псевдогомогенной моделью, уравнение материального баланса может быть представлено в виде:
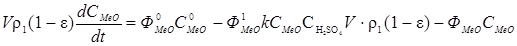 , (5.5)
, (5.5)
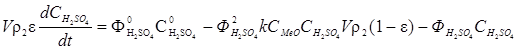 , (5.6)
, (5.6)
где V – объем реакционной смеси; r1, r2 – плотность твердой фазы; e - порозность реакционой смеси; 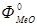 ,
, 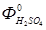 - входные потоки твердого и жидкого вещества;
- входные потоки твердого и жидкого вещества; 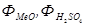 - выходные потоки твердого и жидкого веществ;
- выходные потоки твердого и жидкого веществ; 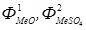 - потоки компонентов реакции, подаваемых в стехиометрических необходимых количествах;
- потоки компонентов реакции, подаваемых в стехиометрических необходимых количествах; 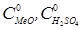 - концентрации веществ во входном потоке; k – константа скорости реакции.
- концентрации веществ во входном потоке; k – константа скорости реакции.
Примем допущения, что гидродинамические условия протекания процесса выщелачивания устойчивы и неизменны, тогда 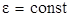 , гидродинамические процессы протекают безынерционно по отношению к химическим, количество твердого и жидкого веществ постоянно:
, гидродинамические процессы протекают безынерционно по отношению к химическим, количество твердого и жидкого веществ постоянно:
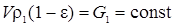 , (5.7)
, (5.7)
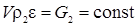 , (5.8)
, (5.8)
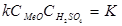 . (5.9)
. (5.9)
Тогда материальный баланс по твердому и жидкому веществам опишется уравнением:
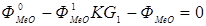 , (5.10)
, (5.10)
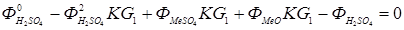 .(5.11)
.(5.11)
В статическом режиме в уравнениях (5.3) и (5.4) производные равны нулю. Тогда, решая совместно уравнения (5.3) и (5.8), (5.4) и (5.9), получим:
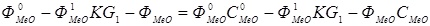 , (5.12)
, (5.12)
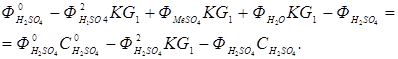 (5.13)
(5.13)
После преобразования получим:
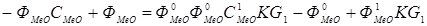 , (5.14)
, (5.14)
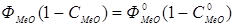 , (5.15)
, (5.15)
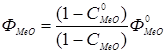 , (5.16)
, (5.16)
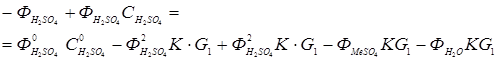 (5.17)
(5.17)
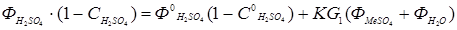 , (5.18)
, (5.18)
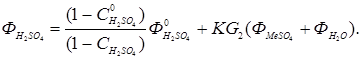 (5.19)
(5.19)
В течение времени похождения пульпы через систему реакторов цинк и сопутствующие ему ценные компоненты должны быть практически полностью переведены в раствор. Вследствие этого извлечение металлов в раствор является основным показателем выщелачивания, который возможно контролировать по степени использования серной кислоты. Для описания процесса выщелачивания используется математическая модель непрерывного гетерогенного процесса. В случае равенства объемов реакторов и с учетом зависимости (5.2) извлечение вещества, достигаемое в каскаде реакторов определяется по уравнению:
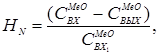 (5.20)
(5.20)
где 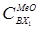 - концентрация оксидов металлов во входном потоке;
- концентрация оксидов металлов во входном потоке; 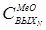 -концентрация оксидов металлов в выходном потоке N-го реактора.
-концентрация оксидов металлов в выходном потоке N-го реактора.
Извлечение металлов в раствор возможно контролировать по степени использования серной кислоты, количество которой практически определяется автоматическими анализаторами. Поэтому можно записать:
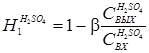 . (5.21)
. (5.21)
Система реакторов выщелачивания функционирует в строго установившемся режиме, причем в каждом из аппаратов системы сохраняют свои определенные и постоянные условия. Так как отдельные элементы пульпы пребывают в системе различное время и некоторые из них «проскакивают» систему очень быстро. Превращение вещества никогда не может быть идеально полным. По этой причине нельзя говорить о каком-либо определенном «времени реагирования». Поэтому при оценке работы непрерывно действующей системы реакторов пользовались понятием среднего времени пребывания пульпы в реакторе. В целях уточнения структуры модели приняты следующие допущения: интенсивность перемешивания пульпы в реакторах обеспечивает ее однородность; состав пульпы в реакторе полностью соответствует ее составу на выходе; время усреднения свежего материала, подаваемого в реактор, пренебрежимо мало по сравнению со временем обработки пульпы; объемная скорость потоков пульпы во внутренней и внешней циркуляции каждого реактора постоянны; при определении степени использования серной кислоты применяются следующие понятия.
1. Номинальное время пребывания частиц пульпы в реакторе:
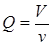 , (5.22)
, (5.22)
где V – объем пульпы в реакторе, v – объемная скорость подачи пульпы.
2. Абсолютное время пребывания отдельных частиц в реакторе или текущее время их реакции t оценивают в натуральных единицах.
3. Безразмерное (относительное) время реакции Т:
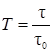 , (5.23)
, (5.23)
где t0 – натуральное время полного или условно полного завершения реакции.
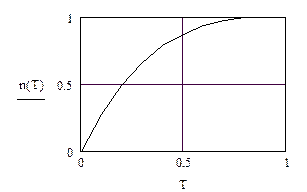
4. Функция превращения вещества h(CT), выражающая долю завершения реакции во времени относительно реагирующего количества:
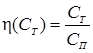 , (5.24)
, (5.24)
где C T , C П – концентрация серной кислоты в получаемом растворе соответственно текущая и предельная.
5. Функция растворения вещества W(CT), выражающая долю недорастворившегося вещества во времени относительно условно полного реагирующего количества:
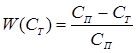 . (5.25)
. (5.25)
6. Интегральная функция распределения Ф(Т), выражающая долю потока пульпы или долю частиц вещества, пребывающих в системе реакторов в течение времени меньшего или равного Т. Остальная часть пульпы 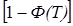 имеет возраст частиц от Т до
имеет возраст частиц от Т до 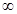 .
.
При введении в реактор объемом V с номинальным временем пребывания в реакторе Q инертный индикатор в момент времени 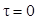 распределившись на пульпе, дает начальную концентрацию C 1, 0. В дальнейшем концентрация индикатора снижается и в некоторый момент t равна С1,t. Соответственно доля элементов пульпы, оставшихся в реакторе и имеющих возраст t, будет характеризоваться отношением
распределившись на пульпе, дает начальную концентрацию C 1, 0. В дальнейшем концентрация индикатора снижается и в некоторый момент t равна С1,t. Соответственно доля элементов пульпы, оставшихся в реакторе и имеющих возраст t, будет характеризоваться отношением 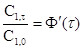 и в момент t устанавливается динамическое равновесие:
и в момент t устанавливается динамическое равновесие:
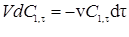 , (5.26)
, (5.26)
которому соответствует выражение
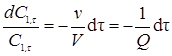 . (5.27)
. (5.27)
Последующее интегрирование с определением постоянной при 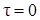 и
и 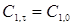 дает:
дает:
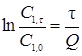 (5.28)
(5.28)
или
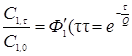 . (5.29)
. (5.29)
Для второго реактора каскада уравнение материального баланса имеет вид:
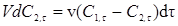 (5.30)
(5.30)
или
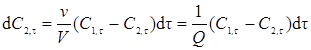 , (5.31)
, (5.31)
где С2,t - текущая концентрация индикатора во втором реакторе.
Используя значение С1,t , получим:
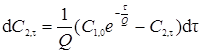 (5.32)
(5.32)
или дифференциальное уравнение первого порядка:
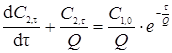 ,
,
решение которого с определением постоянной при 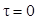 и
и 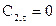 дает:
дает:
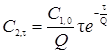 , (5.33)
, (5.33)
и
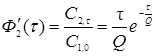 . (5.34)
. (5.34)
В общем случае концентрация индикатора в n – ом реакторе каскада:
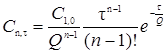 , (5.35)
, (5.35)
а его доля в n – ом реакторе
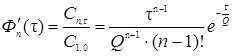 . (5.36)
. (5.36)
7. Дифференциальная функция распределения d Ф(t) и d Ф(Т) выражает долю потока пульпы или долю частиц вещества, пребывающих в системе реакторов в течении времени от t до t + dt или Т + dT. Остальная часть пульпы представлена дифференциальными элементами, возраст которых меньше t и частицами, возраст которых больше (t + dt). Общее содержание всех элементов пульпы будет равно единице:
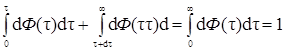 . (5.37)
. (5.37)
или
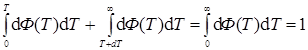 . (5.38)
. (5.38)
Для системы реакторов равного объема, установленных последовательно:
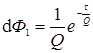 ,
, 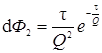 , … ,
, … , 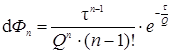 . (5.39)
. (5.39)
Общее извлечение или общие потери определяют интегрированием получаемых произведений по всему диапазону возможных значений t или Т. Соответственно степень использования серной кислоты, достигаемая в каскаде последовательно установленных реакторов, определяется следующим образом:
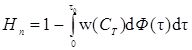 или
или 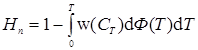 . (5.40)
. (5.40)
3. Содержание работы
В соответствии с вариантом задания с помощью программы, составленной в вычислительной среде MathCAD, провести исследование основных закономерностей процесса выщелачивания.
| Программа |
| 1. Натуральное время полного или условно полного завершения реакции |
| t0:=6 |
| 2. Текущее время реакции |
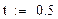
|
| 3.Относительное время реакции |
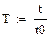 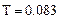
|
| 4. Функция превращения вещества |
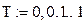
|
|
|
| 5. Функция растворения вещества |
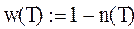
|
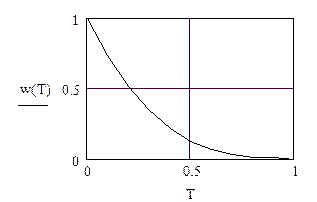
|
6. Объем реактора 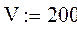
|
7. Объемная скорость подачи раствора 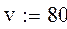
|
| 8. Расчетное время пребывания раствора в каждом аппарате |
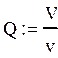 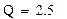
|
| 9. Коэффициент времени |
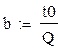 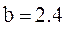
|
| 10. Число реакторов в каскаде |
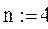
|
| 11. Интегральная функция распределения |
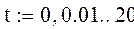
|
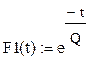 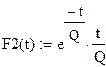 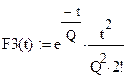 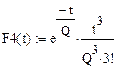
|
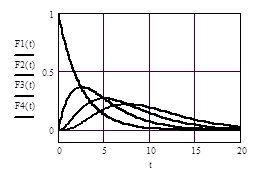
|
| 12. Дифференциальная функция распределения |
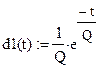 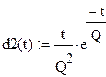 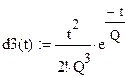 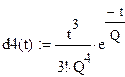
|
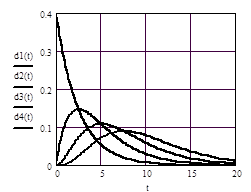
|
| 13. Определение степени превращения вещества в реакторах |
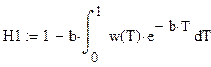 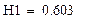
|
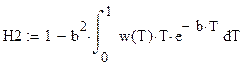 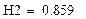
|
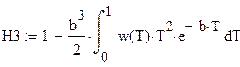 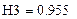
|
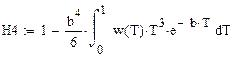 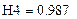
|
3. Задание для выполнения
| Вар. | 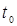
| 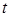
| 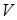
| 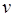
| 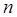
|
| 1 | 6,5 | 0,5 | 200 | 80 | 5 |
| 2 | 6 | 0,550,5 | 150 | 70 | 4 |
| 3 | 5,5 | 0,49 | 140 | 75 | 6 |
| 4 | 5 | 0,48 | 160 | 80 | 5 |
| 5 | 4,5 | 0,47 | 170 | 85 | 4 |
| 6 | 4,7 | 0,46 | 180 | 90 | 6 |
| 7 | 4,6 | 0,45 | 190 | 80 | 3 |
| 8 | 5,1 | 0,44 | 200 | 85 | 5 |
| 9 | 5,2 | 0,43 | 190 | 95 | 4 |
| 10 | 5,4 | 0,44 | 180 | 90 | 3 |
4. Содержание отчета
3.1. Тема работы.
3.2. Постановка задачи.
3.3. Расчет основных показателей процесса с помощью математической модели.
3.4. Графики основных показателей процесса выщелачивания: функция превращения вещества, функция растворения вещества, дифференциальная функция распределения, интегральная функция распределения, зависимость извлечения ценного компонента по каскаду реакторов.
3.5. Выводы
5. Контрольные вопросы
5.1. К какому типу относится математическая модель процесса выщелачивания?
5.2. Какие допущения приняты при построении модели?
5.3. В чем состоит смысл функций растворения и превращения?
5.4. Что показывают интегральная и дифференциальная функции распределения?
Лабораторная работа №5
МОДЕЛИРОВАНИЕ РАБОТЫ ЭЛЕКТРИЧЕСКОГО
НАГРЕВАТЕЛЯ И ИССЛЕДОВАНИЕ СИСТЕМЫ
ДВУХПОЗИЦИОННОГО РЕГУЛИРОВАНИЯ
ТЕМПЕРАТРУРЫ
Цель работы: получать практические навыки моделирования работы электрического нагревателя и исследования на его модели системы двухпозиционного регулирования температуры.
6.1. Постановка задачи
Известна мощность нагревателя 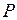 , его масса
, его масса 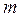 и удельная теплоемкость
и удельная теплоемкость 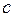 . Потери тепла
. Потери тепла 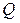 происходят за счет теплопроводности среды и конвекции по закону:
происходят за счет теплопроводности среды и конвекции по закону:
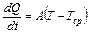 , (6.1)
, (6.1)
где T – температура нагревателя, 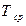 - температура окружающей среды, А – коэффициент
- температура окружающей среды, А – коэффициент
а также за счет излучения в соответствии с законом Стефана-Больцмана:
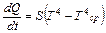 , (6.2)
, (6.2)
где 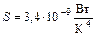 - приведенный коэффициент теплообмена излучением.
- приведенный коэффициент теплообмена излучением.
Нагреватель снабжен терморегулятором, который включает его, если температура 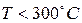 и выключает в случае превышения температуры
и выключает в случае превышения температуры 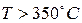 .
.
Математическую модель объекта составим на основании уравнений теплового баланса. Часть подводимой к нагревателю энергии 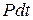 расходуется на его нагрев:
расходуется на его нагрев:
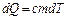 , (6.3)
, (6.3)
а на потери в окружающую среду уходит энергия:
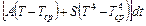 . (6.4)
. (6.4)
Если не учитывать действия терморегулятора, дифференциальное уравнение, описывающее нарастание температуры во времени, имеет вид:
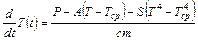 . (6.5)
. (6.5)
6.2. Содержание работы
В данной лабораторной работе необходимо выполнить:
6.2.1. моделирование работы нагревателя без учета системы регулирования,
6.2.2. моделирование системы двухпозиционного регулирования температуры нагревателя.
6.3. Порядок выполнения работы:
6.3.1. Получить вариант задания у преподавателя.
6.3.2. В соответствии с исходными данными решить дифференциальное уравнение математической модели нагревателя. Для решения можно использовать встроенные функции вычислительной среды MathCAD. В примере 1 решения, приведенном ниже, используется функция 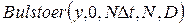 . Данная функция возвращает матрицу решений обыкновенных дифференциальных уравнений методом Булирша-Штера с постоянным шагом с заданными начальными условиями в векторе
. Данная функция возвращает матрицу решений обыкновенных дифференциальных уравнений методом Булирша-Штера с постоянным шагом с заданными начальными условиями в векторе 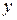 на интервале от 0 до
на интервале от 0 до 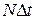 в
в 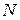 точках. Зададим начальное условие
точках. Зададим начальное условие 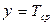 и выразим первую производную:
и выразим первую производную:
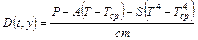 .
.
Пример 1.
| 1. Исходные данные |
Мощность нагревателя 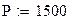
|
Масса нагревателя 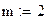
|
Удельная теплоемкость нагревателя 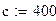
|
Число точек 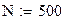
|
Расстояние между точками 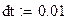
|
Температура окружающей среды 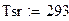
|
Коэффициент 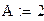
|
Приведенный коэффициент теплообмена излучением 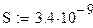
|
| 2. Задаем вектор-функцию |
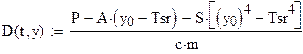
|
3. Задаем начальное условие 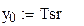
|
| 4. Вызываем встроенную функцию для решения уравнения |
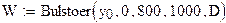
|
| 5. Визуализируем решение |
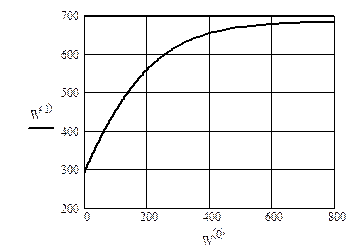
|
Рис. 6.1. Графическое решение дифференциального уравнения
6.3.3. В соответствии с исходными данными провести моделирование двухпозиционной системы регулирования температуры нагревателя. Для моделирования работы системы двухпозиционного регулирования температуры нагревателя уравнение (6.5) решим модифицированным методом Эйлера. Зададим шаг приращения во времени 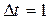 . Возьмем число шагов
. Возьмем число шагов 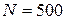 . Тогда функция
. Тогда функция 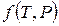 определит производную от температуры по времени:
определит производную от температуры по времени:
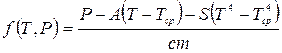 . (6.6)
. (6.6)
Для расчета температуры составлена программа (см. пример 2), реализующая алгоритм ее вычисления и учитывающая действие терморегулятора.
Пример 2.
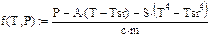
|
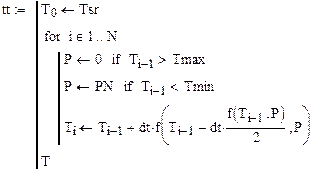
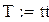
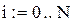
|
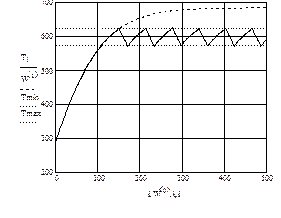 Рис. 6.2. Результат моделирования двухпозиционной системы регулирования
Рис. 6.2. Результат моделирования двухпозиционной системы регулирования
|
6.4. Исходные данные и варианты
Варианты заданий для выполнения приведены в табл. 6.1.
Таблица 6.1.
| Вар. | PN | m | Tsr | A | Tmin | Tmax | dt |
| 1 | 1000 | 1,0 | 290 | 2,0 | 500 | 600 | 1,0 |
| 2 | 1050 | 1,1 | 291 | 2,1 | 510 | 620 | 1,1 |
| 3 | 1100 | 1,2 | 292 | 2,2 | 520 | 640 | 1,2 |
| 4 | 1150 | 1,3 | 293 | 2,0 | 530 | 660 | 1,3 |
| Продолжение таблицы 6.1. | |||||||
| 5 | 1200 | 1,4 | 294 | 2,1 | 540 | 680 | 1,4 |
| 6 | 1250 | 1,5 | 290 | 2,2 | 550 | 700 | 1,5 |
| 7 | 1300 | 1,6 | 291 | 2,0 | 560 | 600 | 1,56 |
| 8 | 1350 | 1,7 | 292 | 2,1 | 570 | 620 | 1,7 |
| 9 | 1400 | 1,8 | 293 | 2,2 | 580 | 640 | 1,8 |
| 10 | 1450 | 1,9 | 294 | 2,0 | 590 | 660 | 1,9 |
| 11 | 1500 | 2,0 | 290 | 2,1 | 600 | 680 | 2,0 |
| 12 | 1550 | 2,1 | 291 | 2,2 | 610 | 700 | 2,1 |
| 13 | 1600 | 2,3 | 292 | 2,0 | 620 | 615 | 2,2 |
| 14 | 1650 | 2,4 | 293 | 2,1 | 630 | 635 | 2,3 |
| 15 | 1700 | 2,5 | 294 | 2,2 | 640 | 645 | 2,4 |
6.5. Требования к отчету.
Отчет по лабораторной работе должен содержать:
6.5.1. Постановку задачи (теоретические сведения),
6.5.2. Номер варианта и исходные данные для расчетов,
6.5.3. Решение дифференциального уравнения, описывающее изменение температуры нагревателя без регулирования,
6.5.4. Результаты моделирования двухпозиционной системы регулирования температуры нагревателя.
6.5.5. Выводы
6.6. Контрольные вопросы
6.6.1. Какие физические явления обусловливают потери тепла нагревателя? В чем состоит их сущность?
6.6.2. Какое уравнение лежит в основе математической модели нагревателя?
6.6.3. По какому принципу осуществляется решение дифференциальных уравнений в системе MathCad?
6.6.4. В чем заключается метод Эйлера для решения дифференциальных уравнений?
6.6.6. В чем заключается принцип двухпозиционного регулирования?
Лабораторная работа №6
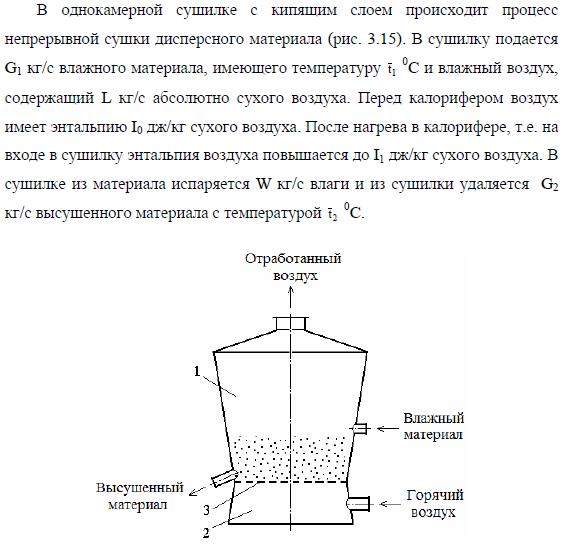
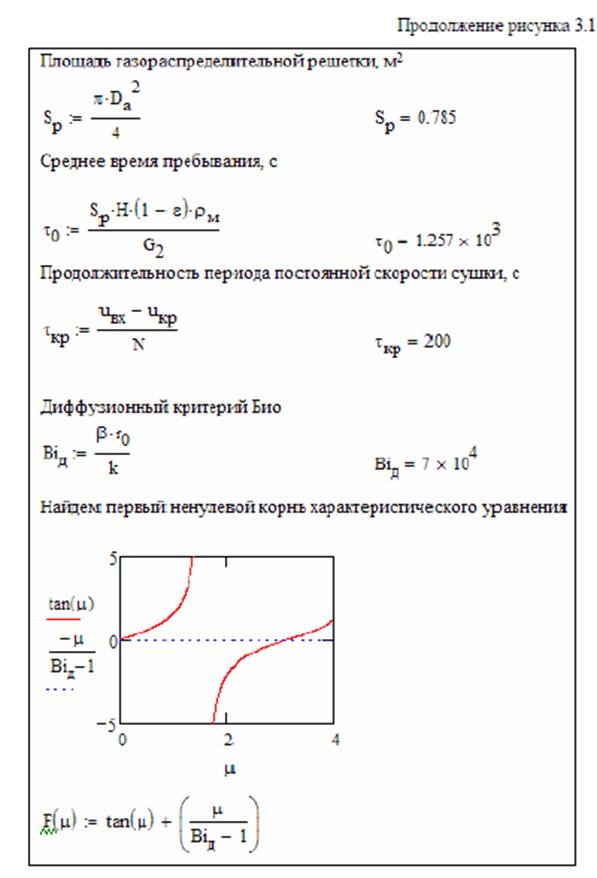
Моделирование сушилки с кипящим слоем
Цель: разработать исследовать математическую модель сушилки с кипящим слоем











Лабораторная работа №7
Моделирование системы регулирования уровня в емкости
Цель работы: разработать и исследовать модель системы регулирования уровня


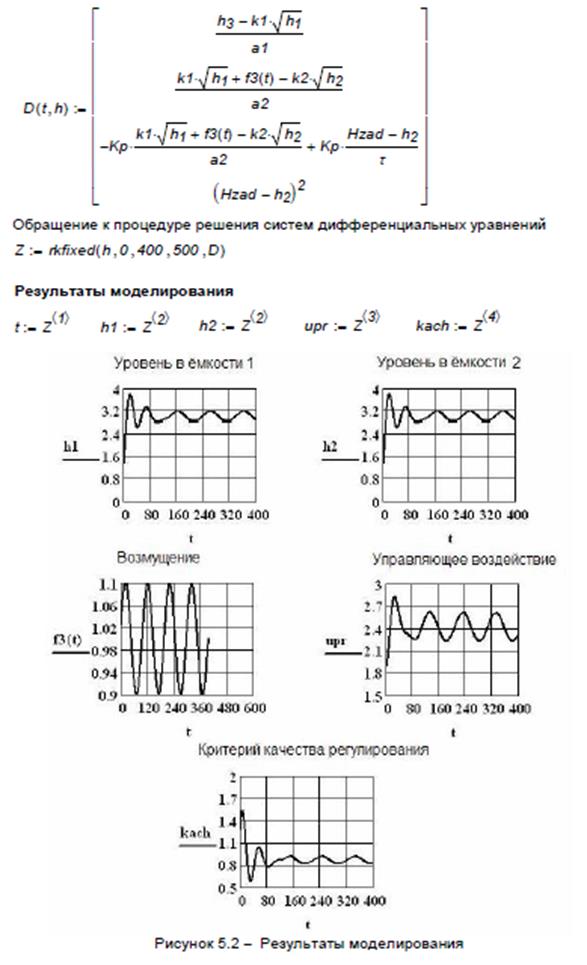
Лабораторная работа №8
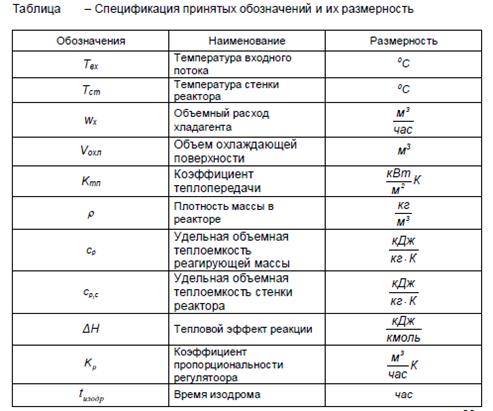
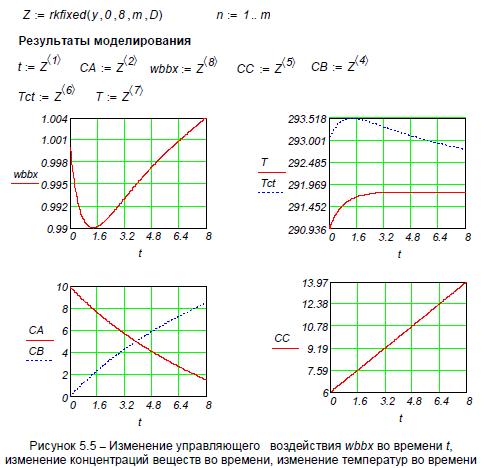
Моделирование системы регулирования температуры в реакторе
Цель: Разработать и исследовать модель системы регулирования температуры в реакторе



Лабораторная работа №9
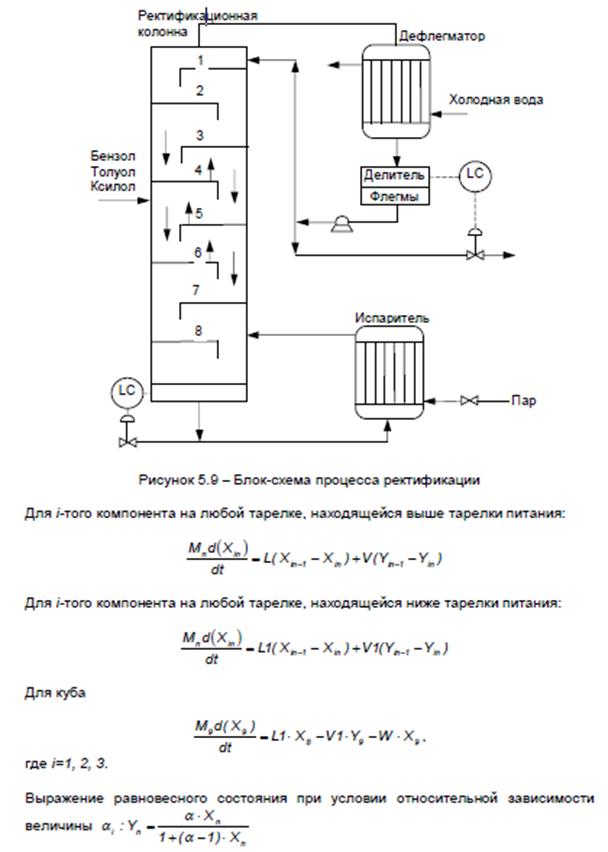
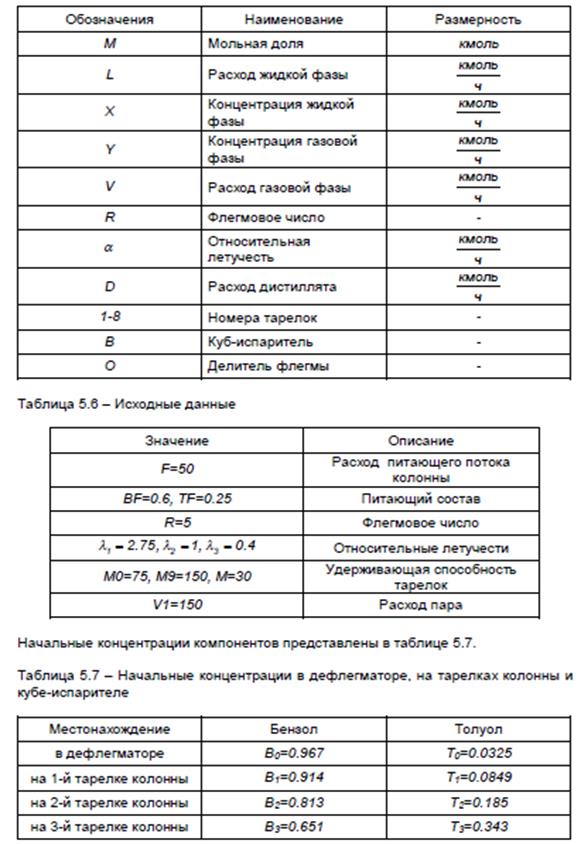
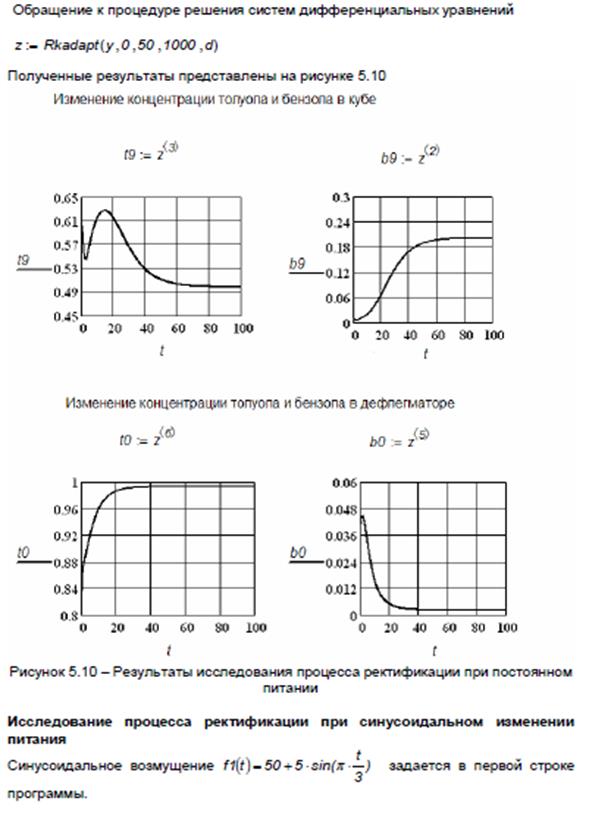
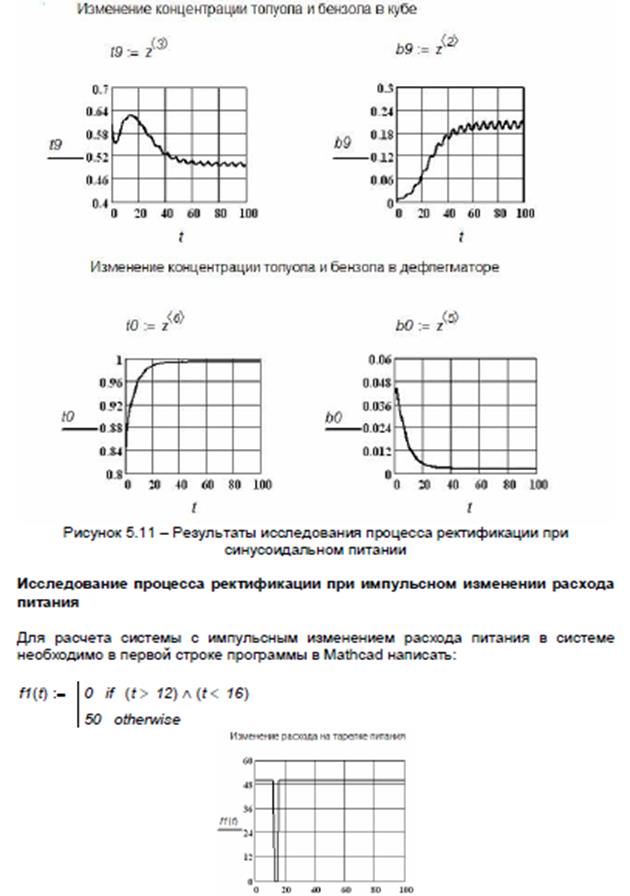
Моделирование процесса управления ректификационной колонной
Цель работы: разработка и исследование модели процесса управления ректификационной колонной



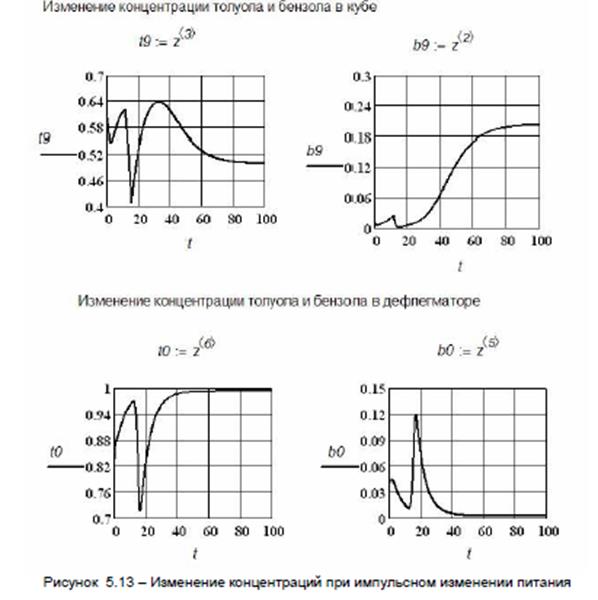









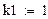 k2:=0.15
k2:=0.15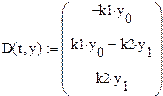
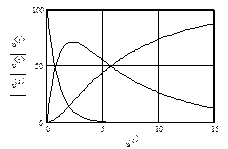
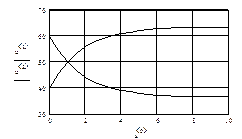
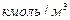
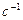
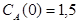
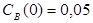
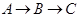
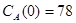 ;
; 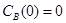 ;
; 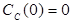
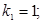
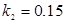
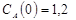
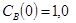
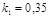
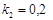
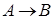
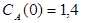
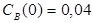
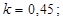
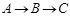
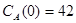 ;
; 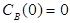 ;
; 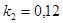
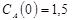
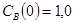
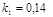
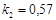
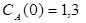
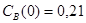
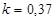
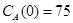 ;
; 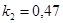
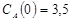
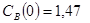
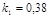
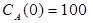
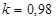
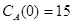 ;
; 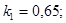
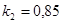
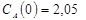
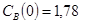
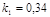
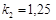
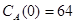 ;
; 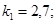
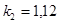
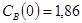
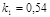
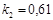
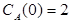
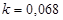
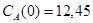 ;
; 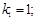
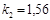
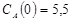
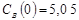
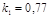
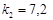
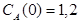
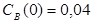
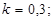
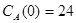 ;
; 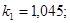
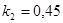
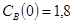
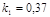
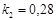
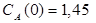
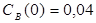
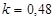
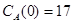 ;
; 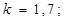
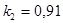
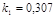
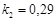
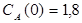
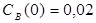
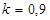
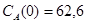 ;
; 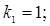
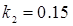
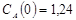
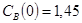
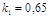
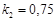
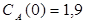
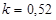
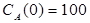 ;
;