Линейные дискретные (цифровые) системы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
ЛАБОРАТОРНАЯ РАБОТА № 7
ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ (ЦИФРОВЫЕ) СИСТЕМЫ
Группа: АТ-13 Преподаватель: доц. Щетинин Ю.И.
Студент: Анисимов А.
Савин М.
г. Новосибирск
2014
Цель работы: изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков их использования в среде.
1. Дискретизация аналогово фильтра:
|
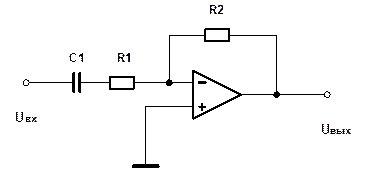
Рис.1. Схема фильтра
Параметры элементов:
R1=1 кОм, R2=2 кОм, C1=0,5 мкФ
1. Дискретизация аналогового фильтра.
Данный фильтр является ФВЧ, т.е. пропускает высокие частоты лучше, чем низкие. Частота среза – частота, при которой АЧХ снижается до уровня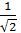 
(что
соответствует 3 дБ) от максимального значения.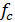 
равна 307 Гц, при выбранных значениях R и С. Верхняя граничная частота дискретного (цифрового) фильтра равна половине частоты отсчетов (дискретизации) 
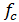. Выберем для данного примера значение 
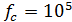Гц, что соответствует интервалу (периоду) отсчетов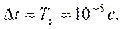 
Передаточная функция данного фильтра, как отношение преобразований Лапласа выходного и входного сигналов, имеет вид:
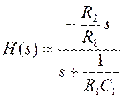
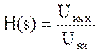
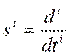
, и
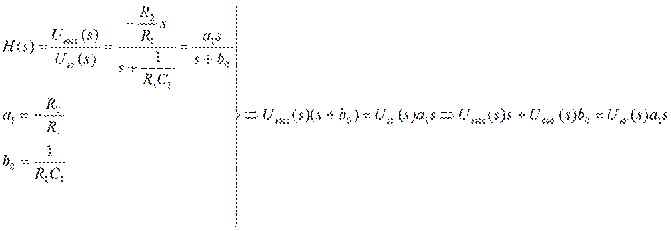
Запишем по виду передаточной функции дифференциальное уравнение, связывающее выходное и входное напряжения фильтра:
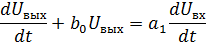
Произведем дискретизацию аналогово фильтра с интервалом отсчетов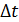 
.
Для этого заменим производную конечной разностью вида:
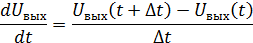
Результат замены:
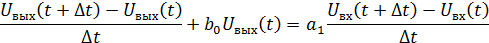
Предположим, что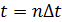 
, 
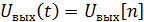и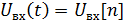 
. Тогда:
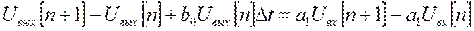
Обозначим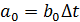 
. Для выбранных числовых значений 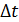, R, C значения коэффициентов равны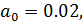 
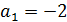. Перепишем уравнение в форме:
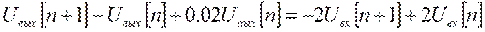
Возьмем Z-преобразование от левой и правой частей уравнения. С учетом теоремы сдвига:
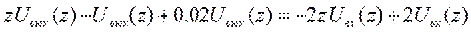
Запишем передаточную функцию дискретного фильтра, как отношение Z-преобразований выходного и входного сигналов:
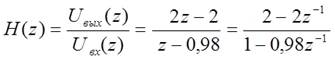
Частотная характеристика дискретной системы представляет собой передаточную функцию при z =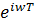 
, то есть:
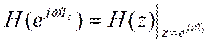
f = 0:0.01:3000;
H1 = 2*j*2*pi*f./(j*2*pi*f+2000);
T=0.00001;
H2 = (2*exp(j*2*pi*f*T)-2)./(exp(j*2*pi*f*T)-0.99);
figure(1)
plot(f,abs(H1),'r',f,abs(H2),'b')
set(gca,'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
xlabel('f, Гц')
set(gca,'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
legend('АЧХ аналогового фильтра','АЧХ дискретного фильтра')
grid
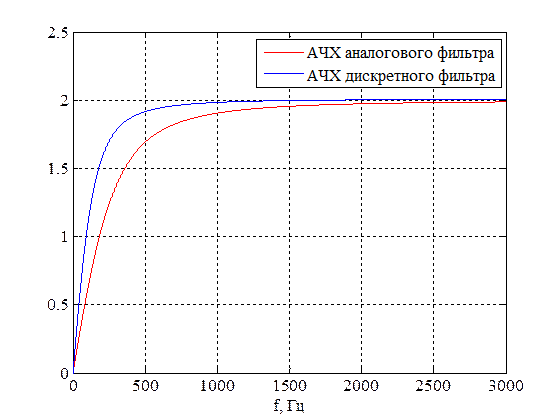
Рис.1 Графики АЧХ аналогового и дискретного фильтров.
АЧХ аналогового и дискретного фильтров соответствуют друг другу, но имеют допустимые расхождения. Следовательно, дискретизация фильтра выполнена верно.
2. Разложение передаточной функции на простые дроби. Получение импульсной характеристики системы.
Воспользуемся следующей последовательностью команд для определения полюсов, вычетов и коэффициентов целой части:
num = [2 -2];
den = [1 -0.98];
[r,p,k] = residuez(num,den)
Результат:
r = 4.0408
p = 0.9800
k = -2.0408
Общий вид разложения:
=
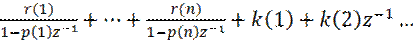
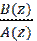
В этой форме представления передаточная функция описывается:
· R вектором – столбцом r вычетов передаточной функции
· P вектором – столбцом p полюсов передаточной функции
· К вектором – строкой k коэффициентов целой части дробно – рациональной функции.
В итоге получили:
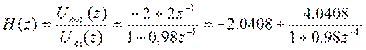
Учитывая что передаточная функция связана с импульсной характеристикой обратным Z – преобразованием, H(z) = Z{h(n)} получим:
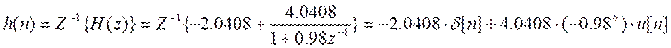
Построим график импульсной характеристики:
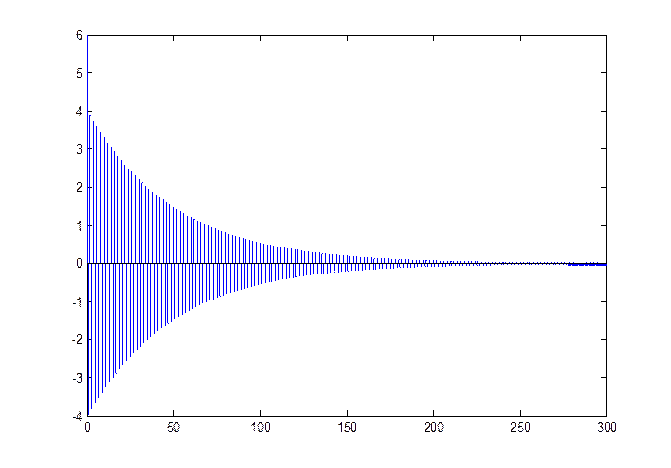
Рис.2 График импульсной характеристики.
Характеристика системы стремится к константе (нулю), значит система устойчива и для ограниченного входного сигнала получим ограниченный выходной сигнал.
3. Нахождение нулей и полюсов дискретной системы.
С помощью следующей программы определим нули и полюса системы и
построим диаграмму полюсов и нулей:
num=[2 -2];
den=[1 -0.98];
nulls = roots(num);
zeros = roots(den);
zplane(num,den)
В результате:
nulls = 1
zeros = 0.98
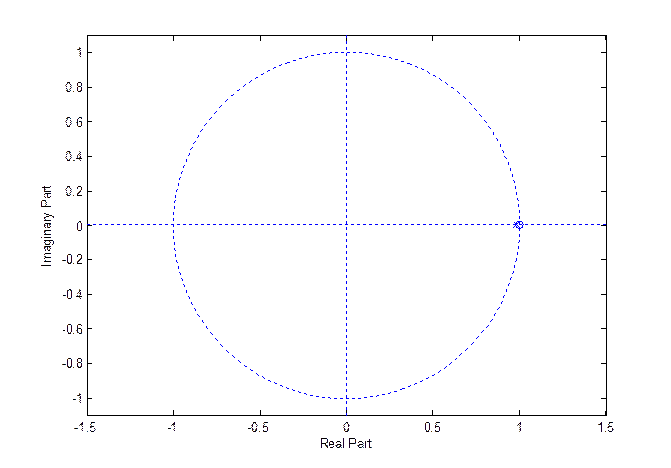
Рис.3Диаграмма нулей и полюсов системы.
Для отображения нолей и полюсов функции передачи фильтра на комплексной плоскости используется функция zplane(). Поскольку при переходе от преобразования Лапласа к Z – преобразованию левая полуплоскость отображается во внутреннюю часть окружности единичного радиуса, а мнимая ось – в единичную окружность (которая показывается функцией zplane (), то для устойчивости дискретной системы необходимо, чтобы полюса её ПФ располагались внутри этой окружности. Полюса и нули лежат внутри единичной
окружности - система устойчива, что соответствует виду импульсной характеристики.
4. Расчет частотной характеристики. Определение частоты среза.
Используем функцию freqz(), для получения частотной характеристики:
num=[2 -2];
den=[1 -0.98];
[H f] = freqz(num,den,1000,10^5);
freqz(num,den,1000,10^5)
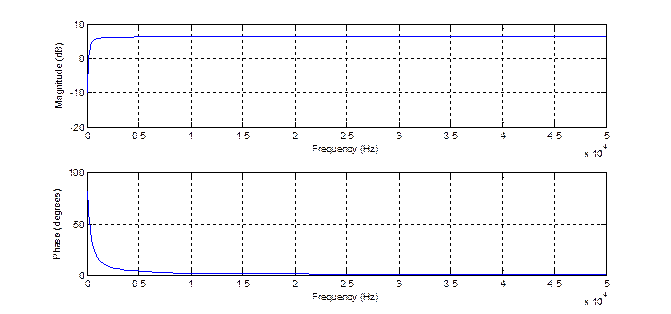
Рис.4 Графики АЧХ и ФЧХ фильтра.
Получим частоту среза:
min = 5;
for i = 1:1:1000
if abs(abs(H(i))-max(abs(H))/sqrt(2))> min;
min = abs(abs(H(i))-max(abs(H))/sqrt(2));
count = i;
end
end
disp ('--------------частота среза------------')
f(count)
angle(H(count))*57.296
min
disp ('---------------------------------------')
Результаты:
ans = 300
ans = 46.9829
min = 0.0503
Система действительно является фильтром верхних частот.
5. Исследование свойства фильтрации системы
Демонстрация фильтрирующего свойства системы:
Fd =10^5; %Hz
f_out = 50;
f_in = 1000; %Hz
n=0:2000;
x=cos(2*pi*f_in*n/Fd); %первый сигнал - в полосе пропускания
subplot(4,1,1)
plot(n./Fd,x),grid;
set(gca,'FontName','Arial Unicode MS','FontSize',9);
xlabel('сек');
y=cos(2*pi*f_out*n/Fd);%второй сигнал - в полосе задержания
subplot(4,1,2)
plot(n./Fd,y),grid;
set(gca,'FontName','Arial Unicode MS','FontSize',9);
xlabel('сек');
Rez=x+y;
subplot(4,1,3), plot(n./Fd,Rez),grid;
set(gca,'FontName','Arial Unicode MS','FontSize',9);
xlabel('сек');
num= [2 -2];
den= [1 -0.98];
F=filter(num,den,Rez);
subplot(4,1,4), plot(n./Fd,F),grid;
set(gca,'FontName','Arial Unicode MS','FontSize',9);
xlabel('сек');
figure(2);
r = dlsim(num,den,Rez);grid;
hold on
plot(n./Fd,Rez,'r');
plot(n./Fd,r);
hold off;
set(gca,'FontName','Arial Unicode MS','FontSize',9);
title('Демонстрация фильтрующих свойств (с исп-ием функции dlsim)')
legend('До фильтра','После фильтра')
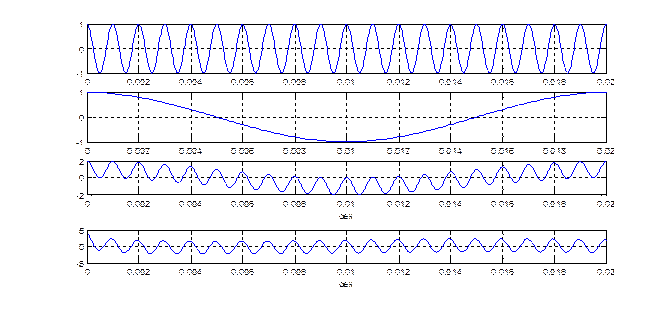
Рис.5.1 Демонстрация фильтрующего свойства системы, с использованием функции filter().
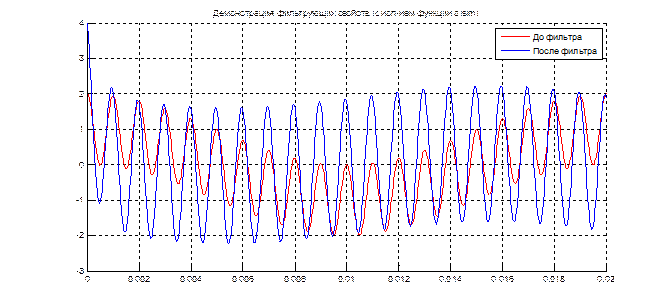
Рис.5.2 Демонстрация фильтрующего свойства системы, с использованием функции dlsim().
6. Исследование влияния расположения нулей и полюсов на частотную характеристику системы.
Исходные значения нулей и полюсов
nulls=1
zeros=0.98
Общий вид передаточной функции для дискретной системы
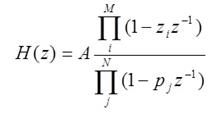
А следовательно, выражение для АЧХ:
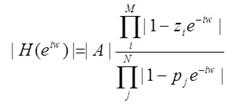
Выражение для АЧХ при одном нуле и одном полюсе
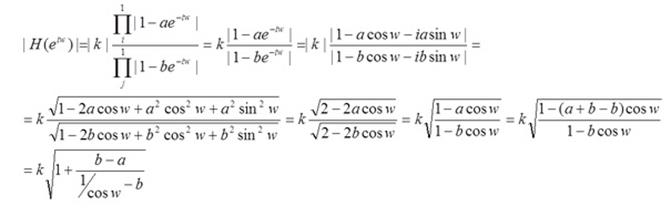
Изменение значений нулей и полюсов
[NUM,DEN] = ZP2TF(0, 0, 2)
NUM = 2 0
DEN = 1 0
[H f]=freqz(NUM,DEN,1000,10^5);
freqz(NUM,DEN,1000,10^5)
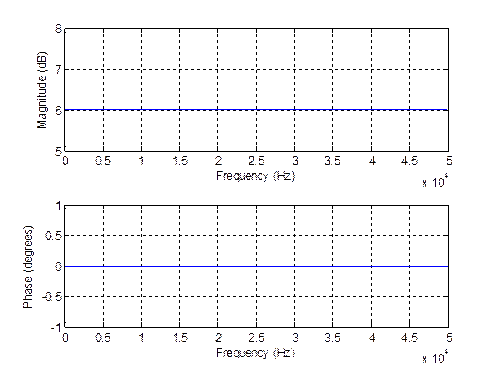
Рис.6.1. График АЧХ для измененных значений нулей и полюсов.
[NUM,DEN] = ZP2TF(-1, 0.5, 2)
NUM = 2 2
DEN = 1.0000 -0.5000
[H f]=freqz(NUM,DEN,1000,10^5);
freqz(NUM,DEN,1000,10^5)
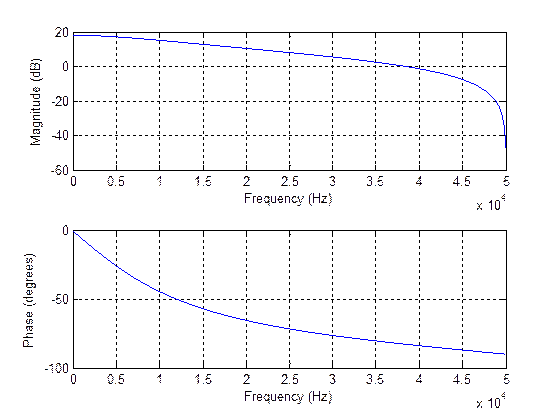
Рис.6.2. График АЧХ для измененных значений нулей и полюсов.
АЧХ системы можно построить, зная расположение её нулей и полюсов. При уменьшении действительного значения полюса частотные характеристики более пологие. Значение полюса нельзя увеличить таким образом, чтобы оно стало более единицы, поскольку система станет неустойчивой.
7. Определение и построение импульсной характеристики с помощью функций impz () и dimpulse ().
num=[2 -2];
den=[1 -0.98];
figure(1);
impz(num,den),grid;
set(gca,'FontName','Arial Unicode MS','FontSize',9);
figure(2);
dimpulse(num,den,100);
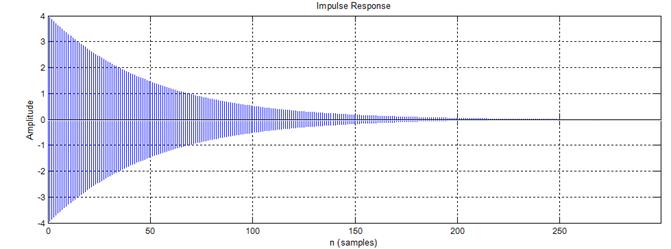
Рис.7.1. График импульсной характеристики, полученный с помощью функции impz().
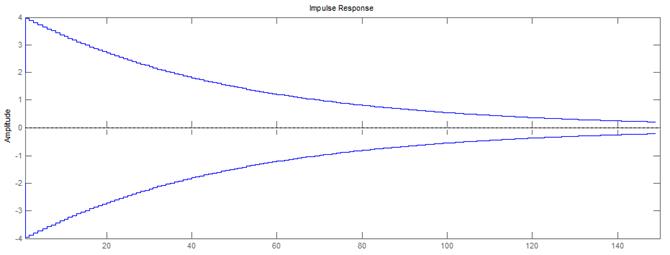
Рис.7.2. График импульсной характеристики, полученный с помощью функции dimpulse ().
Графики импульсных характеристик, полученных с помощью функции impz () и dimpulse () совпадают с импульсной характеристикой цифрового фильтра. Однако преимущество impz () и dimpulse () очевидно - не проводя дополнительных расчетов, можно получить импульсную характеристику системы по передаточной функции. Кроме того, функция dimpulse () имеет возможность удобной навигации по кривой.
8. Построение графика переходной функции с помощью функции dstep ()
C помощью следующей последовательности команд построим график переходной характеристики системы, воспользовавшись функцией dstep().
num=[2 -2];
den=[1 -0.98];
figure(1);
dstep(num,den);
grid;
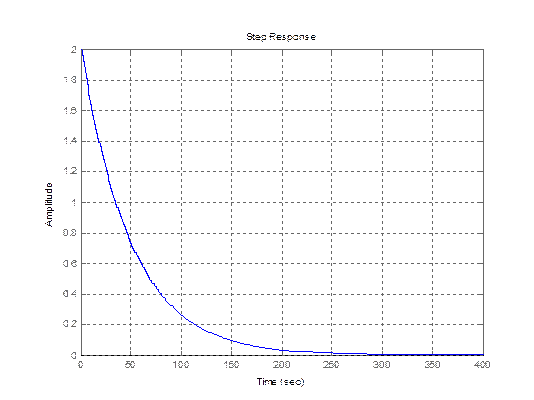
Рис.8. График переходной характеристики, построенной с помощью функции dstep ().
Переходная характеристика – реакция системы на входной сигнал в виде единичной последовательности при нулевых начальных условиях.
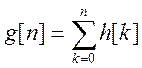- переходная характеристика равна сумме импульсных характеристик.
9. Построение частотной и импульсной характеристик фильтра
C помощью следующей последовательности команд вызовем окно Filter Visualization Tool:
num=[2 -2];
den=[1 -0.98];
fvtool(num,den)
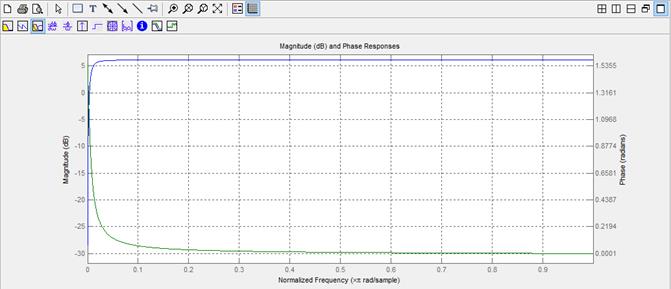
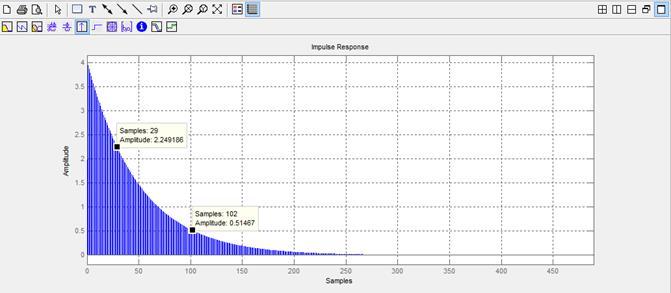
Рис.9 Скриншоты окна Filter Visualization Tool.
Выводы:
Одним из способов получения дискретных фильтров является преобразование аналогового фильтра в дискретный, удовлетворяющий определенным требованиям.
Дискретные линейные стационарные системы описываются линейными разностными уравнениями с постоянными коэффициентами.
Разностное уравнение, описывающее дискретную систему можно получить из
дифференциального уравнения, задающего аналоговую систему, с помощью процедуры дискретизации (замена производных в дифференциальном уравнении конечными разностями).
Такую процедуру мы провели в пункте 1 и проанализировали ее результаты: АЧХ дискретной системы сходится с АЧХ аналоговой системы, которую мы дискретизировали (см. рис. 3)
Также в пункте 1 мы получили передаточную функцию ДС (характеристика систем в области переменной z), использовав обратное Z-преобразование для линейного разностного уравнения системы.
В пункте 2 лабораторной работы, мы разложили передаточную функцию на простые дроби при помощи функции residues(), нашли импульсную характеристику ДС как обратное Z-преобразование передаточной функции системы, построили её график (рис.4) и убедились, что система устойчива.
В пункте 3 мы нашли полюса и нули дискретной системы (в нашем случае – один полюс и один нуль), построив диаграмму (рис.5), получили, что расположение нулей и полюсов соответствует импульсной характеристике (рис.4)
В пункте 4, с использованием функции freqz(), мы нашли АЧХ и ФЧХ исследуемой системы, а также частоту среза.
Исследование свойства фильтрации системы с использованием функций были проведены в пункте 5.
По расположению нулей и полюсов системы на z-плоскости можно судить об её устойчивости, а оперируя значениями нулей и полюсов можно изменять характеристики систем (пункт 6).
График импульсной характеристики, полученной с помощью функции impz() (рис.8) в пункте 7 совпадает с графиком аналитически определённой импульсной характеристики (рис.4) в пункте 2.
Воспользовавшись функцией dstep(), построили график переходной характеристики системы (пункт 8).
Общий вывод: в ходе выполненной лабораторной работы мы преобразовали аналоговый фильтр в дискретный и провели анализ его характеристик и свойств при помощи средств Matlab.