Тема: Структура конечнопорожденных абелевых групп. Структура конечных групп малых порядков.
Лабораторная работа №6
Тема: Структура конечнопорожденных абелевых групп. Структура конечных групп малых порядков.
Основные понятия: внешнее прямое произведение групп; внутреннее прямое произведение подгрупп; структура конечных циклических групп; структура конечнопорожденных абелевых групп; теоремы Силова; описание групп малых порядков.

Задание 1. Указать структуру циклической группы порядка n .
1.1. 36; 1.2. 54; 1.3. 28; 1.4. 98; 1.5. 120; 1. 6. 48;
1.7. 52; 1.8. 64; 1.9. 200; 1.10. 96; 1.11. 150; 1.12. 132 .
Задание 2. Описать (с точностью до изоморфизма) все абелевы группы порядка n . Указать среди них циклические группы.
2.1.100; 2.2. 150; 2.3. 64; 2.4. 132; 2.5. 96; 2.6. 52;
2.7. 48; 2.8. 28; 2.9. 72; 2.10. 120; 2.11. 54; 2.12. 98 .
Задание 3. Разложить в прямую сумму циклических групп фактор-группу 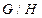 , где
, где 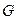 - свободная абелева группа со свободной системой образующих
- свободная абелева группа со свободной системой образующих 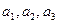 ,
, 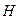 - ее подгруппа, порожденная элементами
- ее подгруппа, порожденная элементами 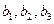 .Указать структуру групп
.Указать структуру групп 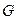 ,
, 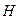 ,
, 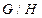 .
.
3.1. 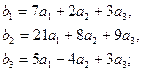 3.2.
3.2. 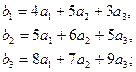 3.3.
3.3. 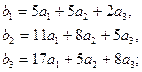
3.4. 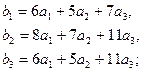 3.5.
3.5. 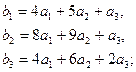 3.6.
3.6. 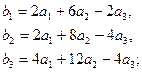
3.7. 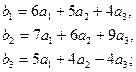 3.8.
3.8. 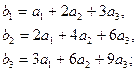 3.9.
3.9. 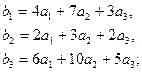
3.10. 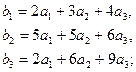 3.11.
3.11. 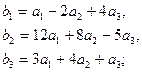 3.12.
3.12. 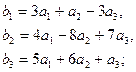
Задание 4. С помощью теорем Силова описать все группы порядка n .
4.1. 10; 4.2. 14; 4.3. 22; 4.4. 26; 4.5. 33; 4.6. 35;
4.7. 45; 4.8. 77; 4.9. 175; 4.10. 185; 4.11. 99; 4.12. 39.
Задание 5.
5.4. Доказать, что порядок элемента прямого произведения конечных групп равен наименьшему общему кратному порядков сомножителей.
5.5. Доказать, что если в абелевой группе подгруппы 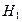 и
и 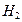 имеют взаимно простые порядки, то их сумма является прямой.
имеют взаимно простые порядки, то их сумма является прямой.
5.6. Пусть 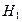 и
и 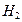 - такие подгруппы группы, что
- такие подгруппы группы, что 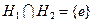 ,
, 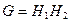 , и все элементы подгруппы
, и все элементы подгруппы 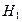 коммутируют с элементами подгруппы
коммутируют с элементами подгруппы 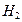 . Доказать, что
. Доказать, что 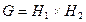 .
.
5.7. Пусть 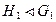 ,
, 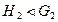 . Доказать, что
. Доказать, что 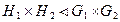 .
.
5.8. Пусть 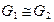 ,
, 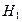 - нормальная подгруппа в
- нормальная подгруппа в 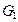 ,
, 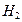 - нормальная подгруппа в
- нормальная подгруппа в 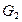 ,
, 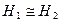 . Доказать, что
. Доказать, что 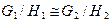 .
.
5.9. Пусть 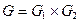 ,
, 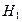 - нормальная подгруппа в
- нормальная подгруппа в 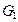 ,
, 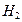 - нормальная подгруппа в
- нормальная подгруппа в 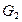 ,
, 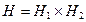 . Доказать, что
. Доказать, что 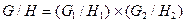 .
.
5.10. Доказать, что прямое произведение групп является абелевой группой тогда и только тогда, когда каждая из этих групп абелева.
5.11. Доказать, что центр прямого произведения равен прямому произведению центров сомножителей.
5. 12. Найти классы сопряженности прямого произведения групп 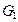 и
и 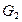 , если известны классы сопряженности групп
, если известны классы сопряженности групп 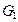 и
и 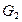 .
.








