Матрица A называется матрицей системы, а вектор–функция b(x) — неоднородностью системы.

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Система Y' = A(x)Y + b(x) называется неоднородной линейной системой дифференциальных уравнений, а система Y' = A(x)Y— однороднойлинейной системой.

Справедлива следующая теорема существования и единственности решения задачи Коши для линейной системы дифференциальных уравнений.

Если A(x) и b(x) непрерывны на отрезке [a, b] , то какова бы ни была начальная точка (x₀, Y₀) из R^{n + 1}, задача Коши Y' = A(x)Y + b(x), Y(x₀) = Y₀,

имеет единственное на [a,b] решение Y = Y(x) .

Важно отметить, что для линейной системы дифференциальных уравнений разрешимость задачи Коши глобальная: решение существует всюду, где непрерывны коэффициенты и неоднородность системы.

2.4 Линейные системы с постоянными коэффициентами

Замечание о собственных числах и собственных столбцах 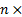-матрицы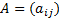

Решаем системы вида

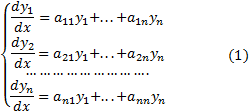
где 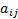-- действительные числа. Будем искать решение в виде

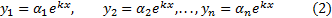
Тогда (2) -- решение (1) в том и только том случае, когда k - собственное число, 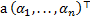-- собственный вектор матрицы 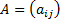. Рассмотрим только один случай -- все собственные числа действительны и попарно различны -- 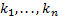. Пусть 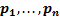-- собственные вектора (столбцы), соответствующие этим собственным числам. Тогда общее решение имеет вид

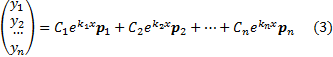
1. Комплексные числа, их изображение. Сопряжение к. чисел. Сложение, умножение и деление комплексных чисел.

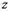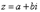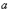Комплексным числом называется число вида , где и 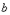– действительные числа, 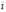– так называемая мнимая единица. Число 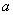называется действительной частью ( 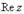)комплексного числа 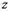, число 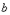называется мнимой частью ( ) комплексного числа .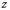

Всякое комплексное число z=x+iy можно изобразить точкой М(х;у) плоскости ОXY такой, что a=Rez, b=Imz.

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=a+0i=a. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+ib.

Сопряжённые числа

Если комплексное число z = x + iy, то число 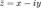называется сопряжённым (или комплексно сопряжённым) к z.

Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.

(сопряжённое к сопряжённому есть исходное)

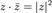
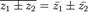
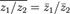
Комплексное сопряжение — операция над комплексным числом, при которой вещественная часть остаётся постоянной, а мнимая — меняет знак.

Сложение

(a + bi) + (c + di) = (a + c) + (b + d)i

Умножение

(a + bi)(c + di) = ac + bci + adi + bdi² = (ac − bd) + (bc + ad)i

Деление

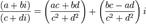
Модуль и аргумент к. числа. Тригонометрическая и показательная формы записи к. чисел. Комплексная экспонента.

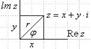
2. Модуль комплексного числа - это длина r вектора изображающего комплексное число z.
Модуль комплексного числа определяется формулой:

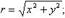
Угол между вектором, изображающим комплексное число z, и осью Re z называется аргументом комплексного числа z.
Аргумент комплексного числа связан с x и y следующими формулами:

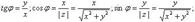
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой

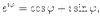которая носит название формулы Эйлера.

Пусть комплексное число 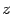в тригонометрической форме имеет вид 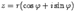. На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим

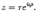
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь , .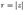

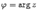Экспонента определяется как аналитическое продолжение экспоненты f(x) = e^x вещественного переменного x.