Теорема. Пусть непрерывны в некоторой односвязной области D . Тогда (1) будет уравнением в полных дифференциалах в том и только том случае, когда в этой области выполнено условие

Дата: 2025-05-01; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

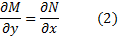
5. Неполные уравнения высших порядков.

6. Линейные дифференциальные уравнения; однородные и неоднородные. Линейность пространства решений однородного линейного уравнения. Общее решение неоднородного линейного дифференциального уравнения.

Дифференциальное уравнение вида

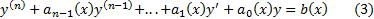
называют линейным неоднородным уравнением или линейным уравнением с правой частью. Если правая часть равна нулю, т.е. если уравнение имеет вид

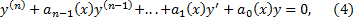
то его называют линейным однородным уравнением. Заметим, что для существования и единственности решения задачи Коши достаточно потребовать непрерывности функций 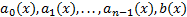. Непрерывность этих функций в дальнейшем предполагается и особо не оговаривается.

В частности дифференциальные линейные уравнения (неоднородное и однородное) второго порядка имеют вид:

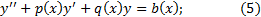
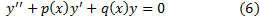
Теорема 1. Сумма двух решений уравнения (6) снова будет решением, и произведение решения на число также будет решением.

Теорема 2. Пусть 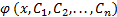-- общее решение однородного уравнения (6), а 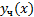-- частное решение неоднородного уравнения (5). Тогда 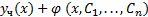есть общее решение неоднородного уравнения (5).

Основная теорема о структуре пространства решений однородного линейного дифференциального уравнения. Пусть 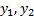—не пропорциональные решения. однородного линейного дифференциального уравнения 2-го порядка. Тогда 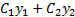есть общее решение этого уравнения.

7. Определитель Вронского. Формула Лиувилля. Основное свойство определителя Вронского. Основная теорема о структуре пространства решений однородного линейного дифференциального уравнения.

Линейное однородное уравнение второго порядка с переменными коэффициентами записывается в виде

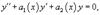
где a₁(x) и a₂(x) являются непрерывными функциями на отрезке [a,b].

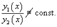
линейно независимые.

Пусть n функций y₁(x), y₂(x), ..., y_n(x) имеют производные (n − 1) порядка. Определитель

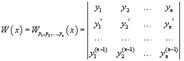
называется определителем Вронского.
Теорема. Если система функций y₁(x), y₂(x), ..., y_n(x) линейна зависима на отрезке [a,b], то ее определитель Вронского тождественно равен нулю на этом отрезке.
Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка [a,b], то функции y₁(x),y₂(x), ..., y_n(x) будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.Формула Лиувилля-Остроградского