Аналогично определяются частные производные высших порядков. Производная называется смешанной.

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Теорема о равенстве смешанных производных. Две смешанные производные одного порядка и отличающиеся друг от друга лишь порядком дифференцирования равны при условии непрерывности этих производных.

Например,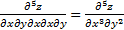

4. Дифференциал ф.м.п. Достаточное условие дифференцируемости. Производная сложной функции. Неявные функции, их дифференцирование.

Определение. Функция 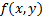называется дифференцируемой в точке 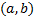, если ее полное приращение можно представить в виде суммы линейной функции от 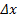и 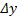и величины бесконечно малой высшего порядка относительно :

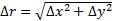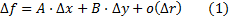
Тогда эта линейная часть 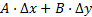называется дифференциалом и обозначается .

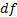ТЕОРЕМА 1. Если функция дифференцируема в точке 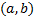, то существуют частные производные в этой точке и .

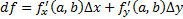Замечание. Взяв находим 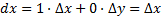. Аналогично, 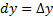. Итак, приращение и дифференциал независимой переменной суть одно и то же. В связи с этим замечанием и теоремой 1 дифференциал приобретает окончательный вид

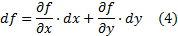
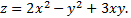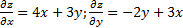Пример. Пусть Тогда и

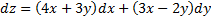
Это функция четырех переменных. Фиксируем точку (1,2). Значение функции 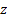в ней равно 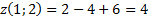, а дифференциал равен 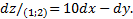Пользуясь этим, найдем приближенно значение 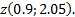Имеем:

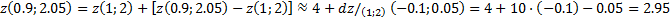
(Точное значение равно 2,9525)

Приближенные вычисления, основанные на понятии дифференциала, используют формулу .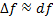

1.1 Достаточное условие дифференцируемости

ТЕОРЕМА 2. Если 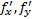существуют и непрерывны в окрестности точки 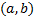, то функция 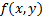дифференцируема в этой точке.

1.2 Производная сложной функции

ТЕОРЕМА 3. Пусть 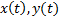--дифференцируемые функции, а 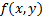имеет непрерывные частные производные в области 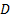. Тогда имеет место формула

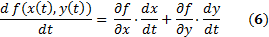
Уравнение касательной плоскости к графику функции 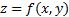в точк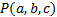е , где 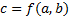имеет вид

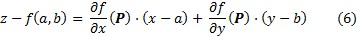
2 Неявные функции

Рассмотрим уравнение

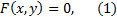
задающее на плоскости Oxy некоторую кривую 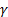. Предполагается, что функция 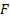имеет непрерывные частные производные. Пусть точка 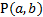удовлетворяет уравнению (1). Тогда ставиться задача – найти непрерывную функцию 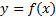такую, что 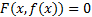тождественно в окрестности точк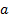и и 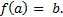Геометрически это значит, что мы локально в окрестности точки 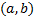, хотим представить кривую 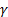как график некоторой функции одной переменной.

ТЕОРЕМА о неявной функции. Пусть 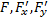определены и непрерывны в окрестности точки 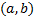, причем 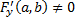. Тогда уравнение (1) определяет (неявную) функцию 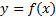такую, что 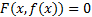тождественно в окрестности точк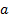и и 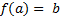. При этом функция 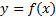дифференцируема в достаточно малой окрестности точк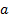и и 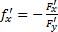в этой окрестности. В частности,

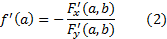
5. Градиент, его геометрический смысл. Касательная плоскость к поверхности. Нормаль к поверхности. Скалярное поле и производная по направлению.

Пусть 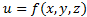– функция (=скалярное поле), определенная в окрестности точк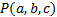и , и 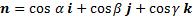-- направление в этой точке, т.е. вектор единичной длины с направляющими косинусами. Производной по направлению n скалярного поля f в точке P называется число

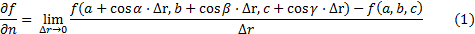
ФОРМУЛА

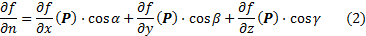
вытекает из правила дифференцирования сложной функции. Правая часть ее есть скалярное произведение вектора n на вектор

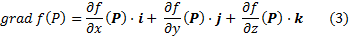
который называется градиентом скалярного поля f в точке P. Точнее правая часть в (2) есть проекция градиента на направление .

grad f |AB|=

A n B

ПРЕДЛОЖЕНИЕ. Производная по направлению в точке P меняется в зависимости от направления от 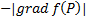до 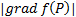. При этом наибольшего значения она достигает в направлении градиента, а наименьшего – в противоположном направлении.

Итак, еще раз

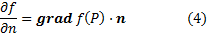
ОПРЕДЕЛЕНИЕ. Пусть точка P фиксирована, а 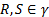причем точки P,R,S не лежат на одной прямой и тем самым определяют плоскость 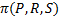называемую секущей. Предел секущих плоскостей при условии 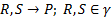называется касательной плоскостью поверхности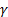

ПРЕДЛОЖЕНИЕ. Градиент перпендикулярен поверхности уровня.

СЛЕДСТВИЕ. Уравнение касательной плоскости к поверхности уровня, проходящей через точку P имеет вид

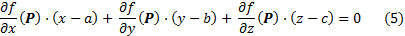
6. Экстремумы ф.м.п. Необходимое условие экстремума. Достаточное условие экстремума функции двух переменных.

Точка 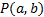называется точкой локального максимума (минимума) функции 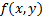, если найдется окрестность 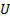этой точки такая, что 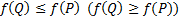для любой 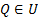. Локальный экстремум – это либо локальный максимум, либо локальный минимум.

Необходимое условие экстремума. В точке экстремума все частные производные равны нулю (если они существуют). Более того, производная по любому направлению равна нулю в такой точке.

Точка 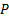, в которой все частные производные, а значит и производная по любому направлению равны нулю, называется стационарной.

ЛЕММА. Квадратичная форма 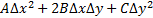положительно определена, т.е. принимает только положительные значения для всех 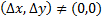, если и только если выполнены условия.

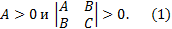
В случае

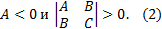
эта квадратичная форма отрицательно определена, т.е. принимает только отрицательные значения при всех .

Достаточное условие экстремума. Пусть Р – стационарная точка функции , т.е. 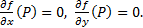Обозначим

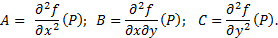
Если выполнено условие (1), то P – точка локального минимума. Если же выполнено условие (2),
то P – точка локального максимума. Если же определитель 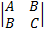меньше нуля, то Р -- седловая точка, и экстремума в этой точке нет.

1. Определение суммы ряда, сходимости и расходимости. Необходимый признак сходимости.

Выражение вида

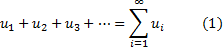
называем рядом; 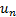-- n-ый член ряда (1). Сумма 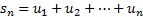называется n-ой частичной суммой ряда (1).

Определение. Суммой ряда (1) называется предел частичных сумм, если 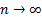. Итак, сумма ряда (1) есть число

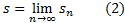
т.е. такое число, что для любого 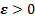найдется натуральное 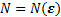начиная с которого, т.е. для любого 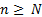выполняется неравенство

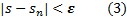
Если существует предел (2), то ряд (1) называется сходящимся. В противном случае, ряд (1) называется расходящимся.

Примеры. а) 0+0+0+… - сходящийся ряд;

б) 𝜺 +𝜺 +𝜺 +… - расходящийся ряд, какое бы малое положительное число 𝜺 мы не взяли;

в) конечная сумма 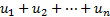превращается в сходящийся ряд, если положить 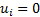при 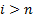; при этом сумма данного ряда равна исходной сумме;

Необходимый признак сходимости.

Теорема. Если ряд 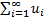сходится то n-ый член 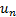стремится к 0 .

Доказательство. . □

2. Геометрическая прогрессия.

- это ряд вида

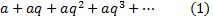
Число q называется знаменателем геометрической прогрессии.

Теорема 2. Пусть 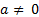. Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна .

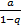3. Арифметические операции с рядами.

Определим сумму двух рядов 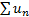и 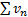как ряд с n-ым слагаемым 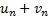. Произведение ряда 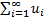на число l - это ряд .

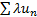Теорема. Если ряды 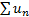и 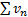сходятся соответственно к s и t, то сумма этих рядов сходится к числу s+t, а произведение ряда 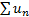на число l сходится к .

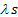Доказательство вытекает из соответствующих свойств предела.

4. Теорема сравнения. Предельная теорема сравнения.

Лемма. Пусть дан ряд с неотрицательными слагаемыми. Тогда этот ряд сходится тогда и только тогда, когда его частичные суммы ограничены сверху.

Теорема сравнения. Пусть 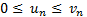для любого натурального n начиная с некоторого номера 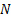. Если ряд 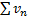сходится, то и ряд 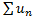сходится. Если же ряд 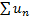расходится, то ряд 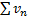также расходится.

Следствие. Пусть 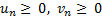для любого натурального n, начиная с некоторого номера, и существует отличный от 0 предел отношения 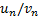. Тогда ряды 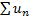и 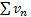ведут себя одинаково в смысле сходимости (либо оба сходятся, либо оба расходятся).

5. Интегральный признак сходимости. Оценка остатка ряда. Ряды вида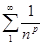

Теорема (интегральный признак сходимости Коши). Пусть 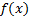- монотонно убывающая, непрерывная и неотрицательная функция при 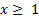. Положим 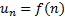для всех натуральных n. Тогда ряд 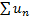и интеграл 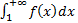ведут себя одинаково в смысле сходимости. При этом имеет место следующая оценка остатка ряда :

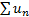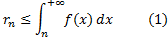
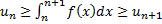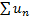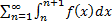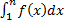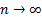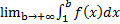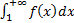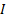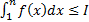Имеем (*). Если ряд сходится, то и ряд сходится по теореме сравнения. Отсюда следует, что интеграл имеет предел при . Из этого вытекает, что существует предел . Это доказывает сходимость интеграла . Наоборот, если последний интеграл сходится и равен , то для любого 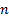. Отсюда и из неравенств (*) следует ограниченность частичных сумм ряда. По лемме Пусть дан ряд с неотрицательными слагаемыми. Тогда этот ряд сходится тогда и только тогда, когда его частичные суммы ограничены сверху вытекает сходимость ряда 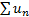. Оценка остатка ряда 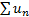следует из неравенства (*):

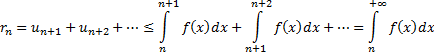
Следствие. Ряд 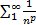сходится тогда и только тогда, когда 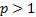. В частности, гармонический ряд расходится.

6. Признаки Даламбера и Коши сходимости знакоположительного ряда.

Признак Даламбера.

Пусть 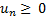для всех достаточно больших натуральных n и существует предел отношения 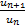, который мы обозначим через d. Если 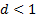, то ряд 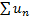сходится; если же 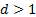, то ряд 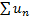расходится.

Радикальный признак Коши: Рассмотрим положительный числовой ряд 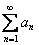. Если существует предел: 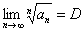, то:
а) При 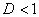ряд сходится. В частности, ряд сходится при .
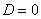б) При 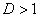ряд расходится. В частности, ряд расходится при .
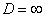в) При 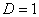признак не дает ответа.

7. Теорема Лейбница о сходимости знакочередующегося ряда. Оценка остатка такого ряда.

Ряд вида

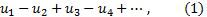
где все 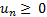, называется знакочередующимся.

Теорема Лейбница. Если последовательность 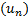монотонно убывает и стремится к 0, то ряд (1) сходится, причем его сумма меньше .

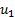Следствие. Остаток ряда (1) меньше первого отброшенного слагаемого.

Пример. Для того, что бы подсчитать

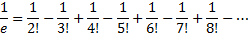
с точностью 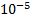надо взять всего лишь 7 слагаемых, ибо 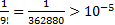. Итак

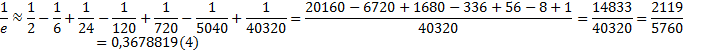
Более точное (калькуляторное) значение -- 0,36787944

8. Абсолютная и условная сходимость. Теорема о сходимости абсолютно сходящегося ряда.

Абсолютная сходимость.

Дан ряд 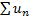с произвольными слагаемыми. Рассмотрим ряд

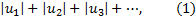
составленный из абсолютных величин членов исходного ряда.

Теорема. Если ряд (1) сходится, то и исходный ряд сходится.

Определение. Ряд 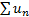такой, что ряд (1), составленный из абсолютных величин сходится, называется абсолютно сходящимся. Если же ряд (1) расходится, а сам ряд 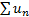сходится, то ряд 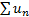называют условно сходящимся.

9. Функциональные ряды. Равномерная сходимость, мажорируемость ряда. Непрерывность суммы функционального ряда.

Ряд вида

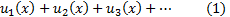
называется функциональным. Областью сходимости этого ряда называется множество всех чисел 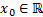, при которых числовой ряд 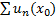сходится.

Здесь 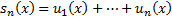-- частичные суммы ряда (1).

Ряд (1) называется мажорируемым на области D, если существует сходящийся числовой ряд 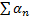(мажоранта) такой, что 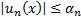для любого n и для любого .

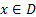Признак равномерной сходимости Вейерштрасса. Если ряд мажорируем в области 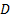, то он сходится равномерно в этой области.

Под промежутком понимается либо интервал, либо полуинтервал, либо отрезок.

Теорема. Если ряд (1) сходится равномерно на промежутке 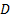, и члены ряда 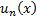непрерывны, то и функция 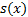непрерывна.

10. Почленная интегрируемость и дифференцируемость функциональных рядов.

Теорема о почленном интегрировании. Пусть ряд 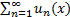с непрерывными слагаемыми, мажорируем на отрезке 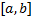и сходится к функции 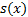. Тогда

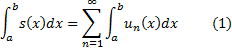
(тем самым числовой ряд в правой части (1) сходится).

Теорема о почленном дифференцировании. Пусть 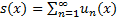, функции 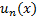непрерывно дифференцируемы и ряд 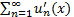мажорируем на отрезке 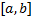. Тогда функция 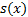также дифференцируема на отрезке 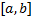и имеет место равенство

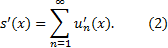
11. Степенные ряды. Интервал и радиус сходимости степенного ряда. Дифференцирование и интегрирование степенных рядов.

Функциональный ряд вида

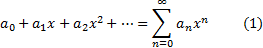
называется степенным рядом. Исследуем ряд (1) на абсолютную сходимость с помощью признака Даламбера:

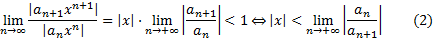
Обозначим

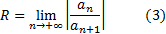
и назовем это число радиусом сходимости ряда (1). Из выкладок (2) и признака Даламбера вытекает, что ряд (1) абсолютно сходится при 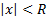, т.е. в интервале 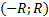и расходится при условии 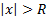. Поведение ряда (1) в точках 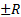исследуется особо.

Более общие степенные ряды, по степеням 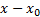имеют вид:

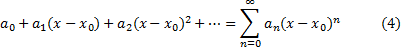
Линейной заменой переменной 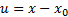они сводятся к рядам вида (1). Интервалом абсолютной сходимости ряда (4) является интервал 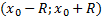, где 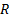– радиус сходимости ряда 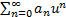. Поведение ряда (4) в точках 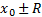исследуется особо.

Дифференцирование и интегрирование степенного ряда

Пусть

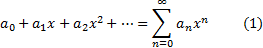
-- степенной ряд с радиусом сходимости R.

Лемма 1. Ряд (1) мажорируем на любом отрезке [a,b] лежащем в интервале сходимости.

Лемма 2. Ряд 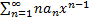, полученный из ряда (1) почленным дифференцированием, имеет тот же радиус сходимости, что и исходный ряд.

Теорема. Пусть 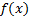-- сумма ряда (1) на интервале 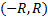. Функция 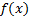бесконечно дифференцируема на этом интервале и её k-ая производная равна сумме k-ых производных членов ряда (1):

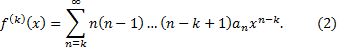
При этом ряд, стоящий в правой части (2) имеет тот же радиус сходимости R. Далее,

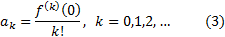
Кроме того, ряд (1) можно почленно интегрировать на любом отрезке 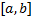, лежащем в интервале сходимости. В частности,

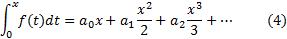
для любого 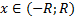и ряд, стоящий в правой части (4), имеет тот же радиус сходимости .

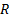12. Ряды Тейлора и Маклорена. Разложение элементарных функций в ряды Маклорена.

Пусть здесь 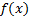-- бесконечно дифференцируемая функция. Тогда степенной ряд формулы Тейлора будет выглядеть:

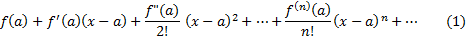
называется рядом Тейлора функции 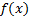в окрестности точки 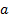. В частном случае, когда 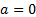, этот ряд называют рядом Маклорена.

Предложение. Ряд Тейлора (1) сходится к 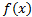тогда и только тогда, когда .

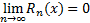Вообще говоря, ряд Тейлора может расходится в точках сколь угодно близких к точке 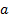или может сходится, но не к функции 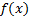. Например функция

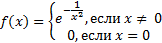
бесконечно дифференцируема в нуле и имеет все производные равные нулю. Следовательно, ряд Маклорена этой функции - нулевой, и его сумма не равна .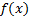

Определение. Если ряд (1) сходится к функции 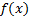в окрестности точки 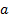, то функцию 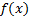называют аналитической в этой точке. Аналитичность функции на множестве означает аналитичность в каждой точке этого множества.

Разложение элементарных функций в ряд Маклорена.

2.1.1 а) Разложение экспоненты

Для всех 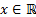имеет место равенство

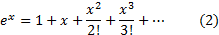
Для доказательства равенства (2) убеждаемся, что

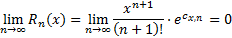
при любом фиксированном 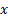и любых величинах 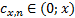. Далее применяем предложение предыдущего параграфа. По другому докажем равенство (2): как функция 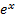, так и сумма ряда в (2) - решения дифференциального уравнения 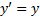с начальным условием y(0)=1. Из теоремы единственности решения дифференциального уравнения следует, что в этом случае функции совпадают.

2.1.2 б) Разложение гармоник

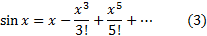
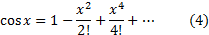
Равенства (3) и (4) можно доказать так же как и для экспоненты, доказав, что остаток в разложении по формуле Маклорена стремится к нулю при 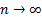. По другому, можно рассуждать так: рассмотрим дифференциальное уравнение 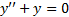с начальными условиями y(0)=0, y'(0)=1 для функции sin x и y(0)=1, y'(0)=0 для функции cos x. Тогда ряды (3) и (4) также как и функции 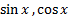-- решения этого диф. уравнения с указанными начальными условиями. По теореме единственности решения диф. уравнения с заданными начальными условиями, получаем совпадение гармоник с рядами (3) и (4). Можно поступить и иначе: подставить в разложение (2) вместо 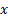чисто мнимое число 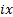, а далее приравнять действительные и мнимые части - получим в точности (3) и (4).

Заметим, что во всех трех равенствах (2),(3),(4) радиус сходимости ряда, стоящего справа равен бесконечности, т.е. разложения имеют место на всей числовой оси.

13. ???Приближенные вычисления, вычисления определенных интегралов и решения дифференциальных уравнений с помощью рядов.

Вычислим интеграл :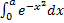

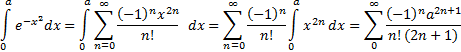
2.2

Решим дифференциальное уравнение 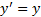c начальным условием 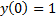. Полагая 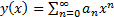и подставляя этот ряд в дифференциальное уравнение, а затем почленно интегрируя, а затем приравнивая коэффициенты при одинаковых степенях, получим

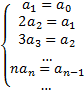
Так как 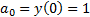, то последовательно находим коэффициенты 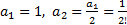, 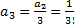и т.д. 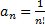. Получаем 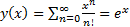. Полученный ряд имеет бесконечный радиус сходимости. Это оправдывает операцию почленного дифференцирования при любом .

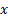1. Общие понятия (определение дифференциального уравнения, решения, порядка, нормальной формы записи). Дифференциальные уравнения 1-го порядка, задача Коши, теорема существования и единственности.

Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).

В этом разделе мы будем решать уравнения, неизвестным в которых ответом является функция. В разделе «Неопределенный интеграл» мы фактически занимались решением уравнения

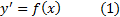
Требовалось найти такую функцию-первообразную 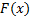, производная которой тождественно равна 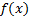. Решений у уравнения (1) бесконечно много, и все они отличаются друг от друга на константу. Эту множественность решений можно обозревать и с другой точки зрения. Фиксируем значение первообразной в определенной точке:

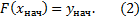
Считаем 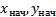начальными условиями. Тогда для непрерывной функции 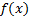, заданной на интервале 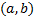и начальных условий 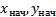c условием 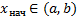существует и единственно решение 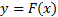уравнения (1), удовлетворяющее соотношению (2). Более того, ответ задается формулой

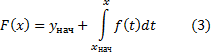
Сформулирована теорема существования и единственности для дифференциального уравнения самого простого вида. Рассмотрим теперь уравнение вида

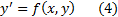
Его полное название – обыкновенное дифференциальное уравнение первого порядка в нормальной форме. Обыкновенное, так как неизвестная функция 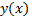зависит лишь от одной переменной, в отличии, например, от уравнения Лапласа 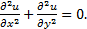Первого порядка – так как старшая производная, входящая в уравнение (4) имеет первый порядок. Нормальная форма записи дифференциального уравнения означает, что старшая производная выражена через младшие производные, а также саму неизвестную функцию, а также переменную. Таким образом,

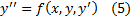
есть дифференциальное уравнение второго порядка в нормальной форме, а

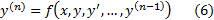
есть общий вид дифференциального уравнения n-го порядка в нормальной форме. Решение уравнений вида (4) составляет основную задачу данной темы. При этом функция 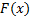называется (частным) решением уравнения (4) или (6), если при подстановки вместо 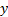в это уравнение получаем тождество.

Задача решения дифференциального уравнения с заданными начальными условиями называется задачей Коши. Начальные условия для уравнения (6) задаются рядом чисел 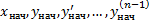и выглядят так

Теорема существования и единственности. Если в дифференциальном уравнении первого порядка(4) функция 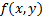вместе со своей частной производной 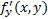непрерывны в области, содержащей 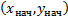как свою внутреннюю точку, то найдется интервал 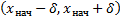для которого, существует и единственно решение 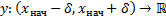задачи Коши.

Общая теорема для уравнения n-го порядка (6) гласит, что если функция 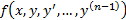вместе со всеми своими частными производными по второй, третьей и т.д. по n-ой переменной непрерывны в пространственной области 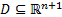, содержащей точку 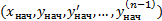, то локальное решение задачи Коши существует и единственно.

2. Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.

2.3 Уравнения с разделяющимися переменными

Дифференциальное уравнение вида

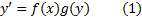
называется уравнением с разделяющимися переменными. Метод решения этого уравнения следующий:

а) записываем производную 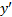в дифференциалах: ;

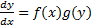б) разделяем переменные и получаем уравнение в дифференциалах : ;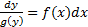

в) интегрируем уравнение в дифференциалах: 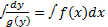(константу C записываем лишь одну) -- получаем общее решение в неявном виде;

г) выражаем y через x и C -- получаем общее решение в явном виде.

Заметим, что такой же метод решения применим и дифференциальному уравнению в дифференциалах, имеющему вид

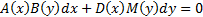
Однородные уравнения

Так называются уравнения вида

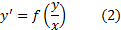
Метод решения: а) переходим к новой неизвестной функции 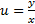. Тогда 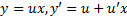и уравнение (2) переписывается так: 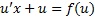(*). А это уравнение с разделяющимися переменными.

б) Решаем вспомогательное уравнение (*). Пусть 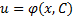есть его общее решение.

в) Тогда 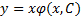-- общее решение исходного уравнения.

3. Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли.

Так называются уравнения вида

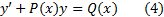
Если P(x), Q(x) непрерывны, то условия теоремы существования и единственности выполнены.

Метод решения

а) Решаем сначала уравнение 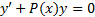без правой части как уравнение с разделяющимися переменными. Получаем общее решение в виде y(x)=C u(x), где 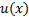-- одна из первообразных функции .

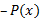б) Общее решение уравнения (4) ищем в виде y=C(x)u(x), где C(x) -- функция, подлежащая определению. Такой приём называется методом вариации постоянных.

в) Подставляя 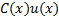в (4), имеем:

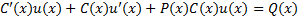
Второе и третье слагаемые в левой части дают 0, ибо 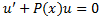. Отсюда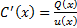

г) Решая это уравнение, т.е. интегрируя, находим

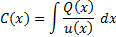
д) Подставляя это в 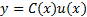, получаем общее решение исходного уравнения.

Обыкновенное дифференциальное уравнение вида:

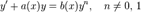
называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение).

Заменим

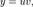
тогда:

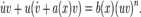
Подберем 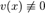так, чтобы было

для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определения 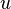получаем уравнение 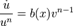— уравнение с разделяющимися переменными.

4. Уравнения в полных дифференциалах.

Дифференциальное уравнение вида

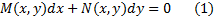
называется уравнением в дифференциалах. Заметим, что (1) действительно дифференциальное уравнение первого порядка, ибо оно может быть переписано для области D, в которой N(x,y)≠ 0 как .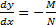

Уравнение (1) назовём уравнением в полных дифференциалах, если в рассматриваемой области существует функция 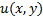, называемая потенциалом, дифференциал которой равен левой части уравнения, т.е.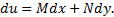

Уравнение в полных дифференциалах может быть переписано в виде du(x,y)=0 общим решением которого являются эквипотенциальные кривые, задаваемые соотношением u(x,y)=C.