Графиком функции двух переменных называется поверхность в пространстве , состоящая из точек таких, что и пробегает всю область допустимых значений функции
1. Определение функции многих переменных; область определения, график, линии и поверхности уровня.
Функция двух переменных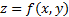 
сопоставляет каждой точке 
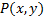некоторой области 
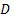на плоскости число 
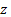по какому-либо закону. Примеры: 1) 
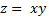– площадь прямоугольника со сторонами 
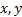. Здесь область 
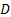задается неравенствами 
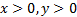. 2) 
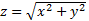- расстояние от точки 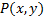до начала координат. Здесь Р – любая точка, и D – вся плоскость Oxy.
Графиком функции двух переменных 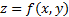называется поверхность в пространстве 
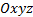, состоящая из точек 
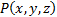таких, что 
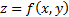и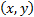 
пробегает всю область допустимых значений функции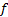 
Линия уровня С функции двух переменных 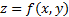задается уравнением 
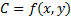. Например, линии уровня 
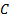функции 
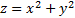не пусты лишь, если 
и представляют из себя концентрические окружности радиуса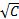 
с центром в начале координат. Линии уровня функции 
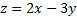-- пучёк прямых, параллельных прямой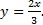 
Функция трех переменных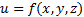 
сопоставляет каждой точке 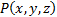из некоторого тела 
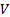число. Например, 
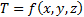-- температура тела в точке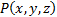
Поверхность уровня С функции 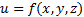задается уравнением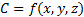 
2. Предел и непрерывность ф.м.п.; их основные свойства. Область – открытое и связное множество. Ограниченные области. Замкнутые области. Теорема Вейерштрасса.
Пусть функция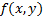 
определена в окрестности точки 
.
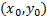Определение. Число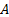 
называется пределом функции 
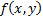при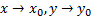 
(записываем как 
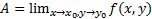), если для любого ε>0 найдется 
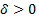, что как только
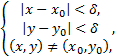
то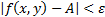 
.
Функция 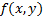непрерывна в точке 
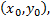если 
. По-другому это можно сформулировать так: полное приращение функции
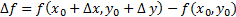
стремиться к нулю, если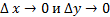 
одновременно.
Свойства:ПР1. Предел суммы двух последовательностей равен сумме пределов, если пределы слагаемых существуют.
Пр2. Любая сходящаяся последовательность 
ограничена.
ПР4. Предел произведения равен произведению пределов, при условии, что пределы сомножителей существуют.
ПР5. Константу можно выносить за знак предела: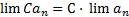 
ПР6. Предел отношения равен отношению пределов, если пределы числителя и знаменателя существуют и последний не равен нулю.
Свойства: LIM1. Константная функция имеет предел, равный этой же константе
LIM2. Предел суммы существует и равен сумме пределов
LIM3. Предел произведения существует и равен произведению пределов:
LIM4. Предел отношения существует и равен отношению пределов в том случае, когда предел знаменателя отличен от 0.
Пусть 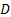область на плоскости. Точку Р назовем внутренней точкой области , если найдется кружок достаточно малого радиуса с центром в точке Р, целиком лежащий в . Точку 
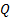назовем внешней точкой области 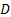, если найдется кружок достаточно малого радиуса с центром в точке 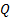, не пересекающийся с 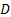. Точку 
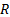назовем граничной для области 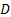, если каждый кружок с центром в точке 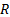пересекается как с 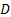так и с дополнением 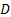. Совокупность всех граничных точек называется границей области 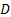и обозначается 
.
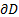Если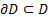 
, то область называют замкнутой, а если ни одна точка из границы не входит в D, то D называют открытой. Бывают не замкнутые и не открытые области. Аналогичные определения внутренних внешних, граничных точек; замкнутости и открытости можно сформулировать в общем случае для подмножеств n-мерного координатного пространства.
Область (тело) называют ограниченной, если ограничены сверху расстояния точек этой области (тела) до начала координат. Иными словами: область ограничена, если ее можно вместить в круг достаточно большого радиуса.
ТЕОРЕМА Вейерштрасса. Пусть функция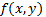 
непрерывна в ограниченной и замкнутой области D. Тогда функция 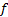ограничена и более того, достигает своего наибольшего и наименьшего значений:
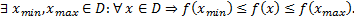
Область 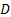называется связной, если любые две точки области можно соединить непрерывной кривой.
3. Частные производные ф.м.п. Частные производные и дифференциалы высших порядков. Теорема о смешанных производных.
Частной производной по 
называется предел отношения частного приращения по к приращению переменной , если последнее (приращение) стремиться к нулю:
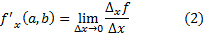
По другому частная производная обозначается как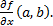 
Техника вычисления частных производных такая же, как и «обычных» производных. Найдем частные производные от функции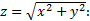 
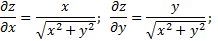
Частные производные от частных производных первого порядка называются частными производными второго порядка.
Частной производной n-го порядка называется частная производная от частной производной (n-1)-го порядка. Частных производных n-го порядка от функции двух переменных 2n штук.