Программируемые логические матрицы
В формальной логике доказано, что любую функцию, заданную таблицей истинности, можно представить в дизъюнктивной нормальной форме – ДНФ (в виде дизъюнкции конъюнкций) и, следовательно, реализовать в схеме, использовав вентили И и ИЛИ.
Для вычисления логических функций в форме дизъюнкции конъюнкций служит так называемая программируемая логическая матрица (ПЛМ).
 |
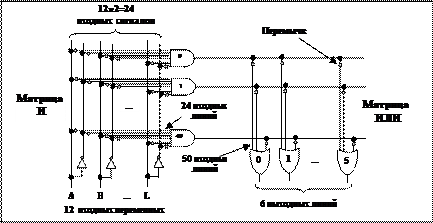Эта микросхема содержит входы для 12 переменных (A,B,…L). Дополнительные сигналы (инверсии) генерируются внутри самой микросхемы, В итоге получается всего 24 входных сигнала.
Какой именно входной сигнал поступает в тот или иной вентиль И, определяется по матрице размером 24 х 50 бит. Каждая из входных линий к 50 вентилям И содержит плавкую перемычку. При выпуске с завода все 1200 перемычек остаются нетронутыми (замкнутыми).
Чтобы запрограммировать матрицу, пользователь – электронщик, пережигает выбранные перемычки, с помощью специального устройства – программатора, прикладывая к схеме высокое напряжение.
Выходная часть схемы состоит из шести вентилей ИЛИ, каждый из которых содержит до 50 входов, что соответствует наличию 50 выходов у вентилей И.
Какие из потенциально возможных связей действительно существуют, зависит от того, как была запрограммирована матрица 50 х 6.
Микросхема имеет 12 входных выводов, 6 выходных выводов, питание и землю (то есть всего 20 выводов).
В качестве примера использования программируемой логической матрицы рассмотрим схему, реализующей функцию большинства.
Она содержит три входа, четыре вентиля И, один вентиль ИЛИ и три инвертора.
Если запрограммировать нашу матрицу соответствующим образом, она сможет вычислять ту же функцию, используя три из 12 входов, четыре из 50 вентилей И и один из 6 вентилей ИЛИ. (Четыре вентиля И должны вычислять произведения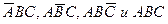 
вентиль ИЛИ принимает эти 4 произведения в качестве входных данных,)
Хотя матрицы, программируемые в эксплуатационных условиях, все еще используются, предпочтение отдается матрицам, которые изготавливаются на заказ. Они разрабатываются заказчиком и выпускаются производителем в соответствии с запросами заказчика. Такие программируемые логические матрицы гораздо дешевле.
Сравним три разных способа реализации функции большинства.
При первом способе, если в качестве компонентов использовать МИС, нам потребуются 4 микросхемы:
1 – сборка с 4 инверторами;
2 – сборки для 4 3-х входовых вентилей И (по два вентиля И на каждый 3-х входовой вентиль И);
1 – сборка с четырьмя вентилями ИЛИ (используется три 2-х входовых вентиля ИЛИ для реализации 4-х входового ИЛИ)
При втором способе можем обойтись одним мультиплексором, построенном на СИС, как было показано ранее.
При третьем способе, мы можем использовать лишь четвертую часть программируемой логической матрицы-
Таким образом, если необходимо вычислять много функций, использование программируемой логической матрицы более аффективно, чем применение двух других методов.
Для простых схем предпочтительнее более дешевые МИС и СИС.
Арифметические схемы
Рассмотрим комбинаторные схемы на СИС, которые используются для выполнения арифметических операций.
Схемы сдвига
 |
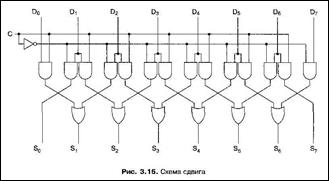Арифметическая схема сдвига, содержащая 8 входов и 8 выходов, имеет вид:
Восемь входных бит подаются на линии D0, D1, …, D7.
Выходные данные, которые представляют собой входные данные, сдвинутые на 1 бит, поступают на линии S0, S0,…, S7.
Линия управления С определяет направление сдвига: 0 — влево, 1 — вправо.
Рассмотрим пары вентилей И (кроме крайних).
Если С = 1, правый член каждой пары включается, пропуская через себя соответствующий бит. Так как правый вентиль И соединен с входом вентиля ИЛИ, который расположен справа от этого вентиля И, происходит сдвиг вправо.
Если С = 0, включается левый вентиль И из пары, и тогда происходит сдвиг влево.
Сумматоры
Схема выполнения операций сложения является существенной частью любого процессора. Таблица истинности для функции сложения одноразрядных целых имеет вид:
 |
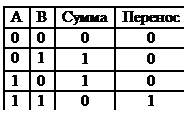Функция имеет две выходные переменные: сумма входных переменных А и В и перенос на следующую (левую) позицию. Схема для вычисления бита суммы и бита переноса, обычно называемая полусумматор 
ом, показана на рисунке
Полусумматор подходит для сложения битов младших разрядов двух многобитовых слов.
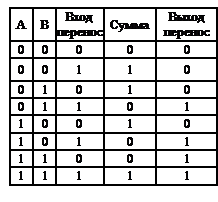
Однако он не годится для сложения битов в середине слова, потому что не может учитывать перенос, возникающий после суммирования битов справа.. Поэтому необходим пол ный сумматор, имеющий следующую таблицу истинности:
Полный сумматор состоит из двух полусумматоров:
 |
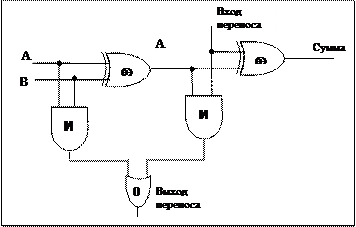