Реализация булевых функций

Дата: 2025-05-01; Просмотры: 5

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Пусть логическая функция от трех пе­ременных: М = f(А, В, С), задана следующей таблицей истинности:

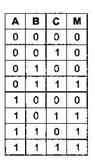
Это функция большинства, которая принимает значе­ние:

· 0, если большинство переменных равны 0,

· 1, если большинство перемен­ных равны 1.

Дизъюнктивная нормальная форма(ДНФ) заданной функции имеет вид:

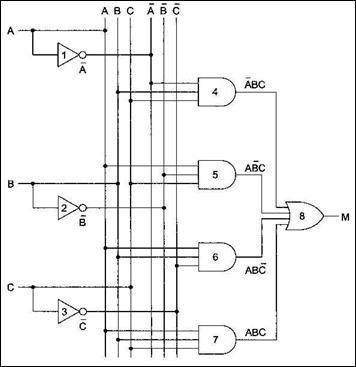Реализация этой функции в виде логической схемы показана на рисунке:

Входные сигналы А, В и С показаны с левой стороны, а функция М_, полученная на выходе, — с правой. Поскольку необходимы дополнительные величины (ин­версии) входных переменных, для их получения сигнал проходит через инверто­ры 1, 2 и 3.

Чтобы сделать рисунок понятней, нарисованы 6 вертикальных ли­ний, 3 из которых связаны с входными переменными, 3 другие — с их инверсиями.

Эти линии обеспечивают передачу входного сигнала к вентилям. Например, вентили 5, 6 и 7 на входе получают сигнал А. В реальной схеме эти вентили будут непосредственно соединены проводом с А без ка­ких-либо промежуточных вертикальных проводов.

Схема содержит четыре вентиля И, - по одному по одному для каждой строки в таблице истинности с резуль­татом 1, или по одному для каждого минитерма ДНФ функции М.

Каждый вентиль И вычисляет одну из указанных строк таблицы ис­тинности или один минитерм ДНФ функции М.

Для получения конечного результата выходы каждого вентиля И соединены с входами вентиля ИЛИ.

Общий алгоритм построения логической схемы для любой булевой функ­ции, заданной таблицей истинности, включает следующие шаги:

1. Составить ДНФ для данной функции (дизъюнкция минитермов, каждый из которых является конъюнкцией всех входных переменных (или их отрицаний) и соответствует строке таблицы истинности с единичным результатом).

2. Включить в схему инверторы, для каждой переменной (входного сигнала), входящей в ДНФ с отрицанием.

3. Нарисовать вентиль И для каждого минитерма ДНФ

4. Соединить вентили И с соответствующими входными сигналами.

5. Вывести выходы всех вентилей И и направить их на вход вентиля ИЛИ.

Этот алгоритм позволяет реализовать любую булеву функцию с помощью вентилей НЕ, И и ИЛИ.

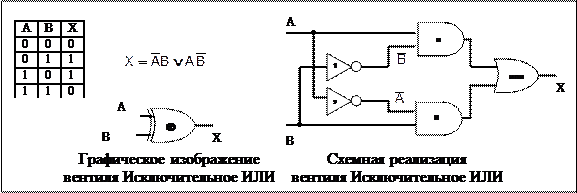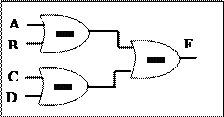
Например. Схемная реализация "Сожжения по модулю два" (исключительное ИЛИ)

Однако часто удобнее строить схемы с использованием одного типа вентилей. Для этого можно преобразовать схемы, построенные по рассмотренному алгоритму, в форму НЕ-И или НЕ-ИЛИ.

Для этого нужно реализовать вентили НЕ, И и ИЛИ с помощью какого-нибудь одного типа вентилей. Один из способов такого преобразования с использованием вентиля НЕ-И или НЕ-ИЛИ показан на рисунке:

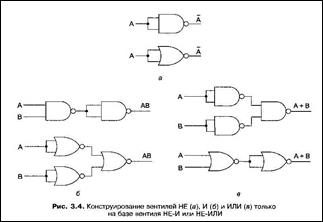Для того чтобы реализовать булеву функцию только на базе вентиля НЕ-И или НЕ-ИЛИ, можно сначала следовать описанному алгоритму, сконструи­ровав схему с вентилями НЕ, И и ИЛИ. Затем нужно заменить многовходовые вентили эквивалентными схемами на двухвходовых вентилях.

Например. 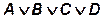можно поменять на 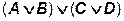, использовав три двухвхо­довых вентиля.

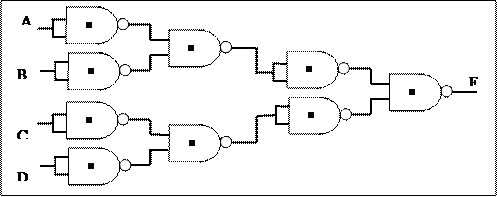Затем каждый двухвходовый вентили НЕ, И и ИЛИ заменяется соответствующей схемой, реализованной на базе только одного типа вентилей, например НЕ-И.

Хотя такая процедура и не приводит к схемам с минимальным количеством вентилей, она показывает возможность подобного преобразования.

Вентили НЕ-И и НЕ-ИЛИ считаются функционально полными, потому что каж­дый из них позволяет вычислить любую булеву функцию.

Ни одни другой вен­тиль не обладает таким свойством, Поэтому именно эти два типа вентилей предпочтительнее при построении логических схем.

Комбинаторные схемы

Многие применения цифровой логики требуют наличия схем с несколькими входами и несколькими выходами, в которых выходные сигналы определяются комбинацией текущих входных сигналов.

Такая схема называется комбинаторной.

Микросхема, которая реализует функцию большинства, является типичным примером комбинаторной схемы. Рассмотрим наиболее часто используемые комбина­торные схемы.

Мультиплексоры

На цифровом логическом уровне мультиплексор представляет собой схему с 2ⁿ входами, одним выходом и п линиями управления, которые позволяют выбрать один из входов. Выбранный вход соединяется с выходом.

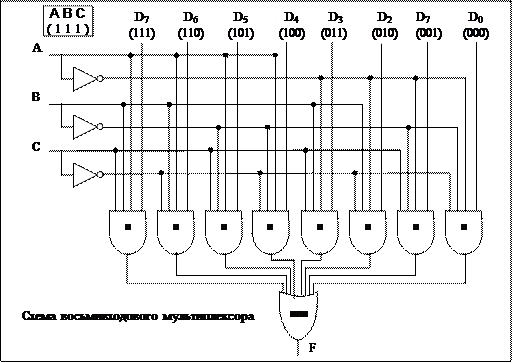На рис, изображена схема восьмивходового мультиплексора (n = 3).

Три линии управления, A, В и С, коди­руют 3-разрядное число, которое указывает, какая из восьми входных линий должна соединяться с вентилем ИЛИ и, следовательно, с выходом F.

Вне зависи­мости от того, какое значение окажется на линиях управления, семь вентилей И всегда будут выдавать на выходе 0, а оставшийся может выдавать 0 или 1 в зави­симости от значения сигнала на выбранной линии входа.

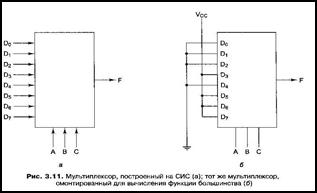Каждый вентиль И запускается определенной комбинацией сигналов на линиях управления. Если в схему муль­типлексора, добавить источник питания и землю, то мультиплексор можно включить в корпус с 14 выводами.

Использовав мультиплексор, мы можем реализовать функцию большинства, как показано на рис. 3,11, б. Для каждой комбинации А, В и С выбирается одна из входных линий. Каждый вход соединяется либо с сигналом V_cc (логическая 1), либо с землей (логический 0). Алгоритм соединения заключается в установлении значения входного сигнал D_i равным значению в строке i таблицы истин­ности.

В таблице истинности функции большинства в строках 0, 1, 2 и 4 значение функции равно 0, поэтому со­ответствующие входы заземляются; в оставшихся строках значение функции равно 1, поэтому соответствующие входы соединяются с логической единицей.

Таким способом можно реализовать любую таблицу истинности с тремя пере­менными, использовав микросхему мультиплексора .

Мультиплексор можно использовать в качестве преобразователя параллельною кода в последо­вательный. Если подать параллельно 8 бит данных на входные линии, а затем поочередно подавать на линии управления, коды от 000 до 111 (это дво­ичные числа), то 8 бит входных данных поступят на выходную линию последовательно.

Такое преобразование осуществляется, например, при вводе информации с клавиатуры. Каждое нажатие клавиши определяет 7- или 8-разрядное число, которое передается процессору последовательно по однопроводной линии.

Декодеры

В качестве второго примера рассмотрим схему, которая получает на входе n-раз­рядное число и использует его для того, чтобы выбрать (то есть установить значение в 1) одну из 2ⁿ выходных линий.

Такая схема называется декодером.
Чтобы понять, зачем нужен декодер, представим себе оперативную память, состоящую из 8 микросхем, каждая из которых содержит 1 Мбайт ячеек хранения данных.

Каждая микросхема имеет адреса в диапазоне от 0 до 1 Мбайт, задаваемые 20 младшими разрядами адреса данных. Три стар­ших двоичных разряда адреса данных используются для выбора одной из восьми микро­схем. На рисунке эти три бита : А, В и С являющиеся входами в декодер.

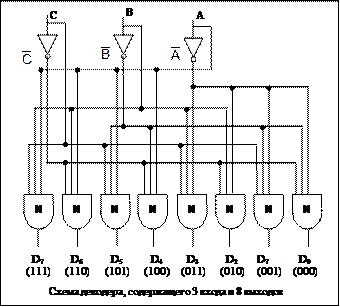В зависимости от входных сиг­налов ровно одна из восьми выходных линий (D0) ..., D7) принимает значение 1; остальные линии принимают значение 0. Поскольку только одна линия принимает значение 1, запускается только одна из восьми микросхем памяти

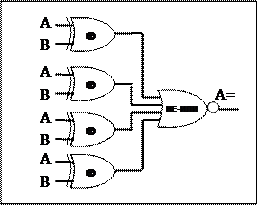Принцип работы схемы, изображенной на рисунке.

Каждый вен­тиль И имеет три входа, из которых первый — это А или 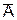, второй — В или 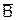третий — С или 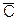. Каждый вентиль запускается различной комбинацией входов; D₀ — сочетанием 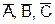, D₁ — сочетанием 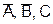и т. д.

Компараторы

Еще одна полезная схема — компаратор. Компаратор сравнивает два слова, ко­торые поступают ему на вход.

Компаратор, изображенный на рисунке, принимает два входных 4 –х битных сигнала, А и В, и выдает 1, если А=B , и 0, ес­ли они не равны А¹B.

Схема основывается на вентиле ИСКЛЮЧАЮЩЕЕ ИЛИ, ко­торый выдает 0, если сигналы на входе равны, и 1, если сигналы на входе не равны.

Если все четыре входных бита слов А и В равны, все четыре вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ будут выдавать 0. Эти четыре сигнала затем поступают в вентиль НЕ-ИЛИ. Если в результате получается 1, значит, слова, поступившие на вход, равны; в противном случае они не равны.