Глава III. Примеры нахождения характерных величин для сложных поверхностей
3.1 Тор
Тор – поверхность, которая получается при вращении окружности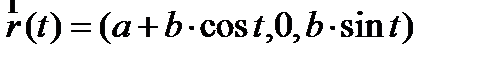 
вокруг оси oz. Тогда используя формулу (2) и (3) получим параметризацию сферы (см. рис.6):
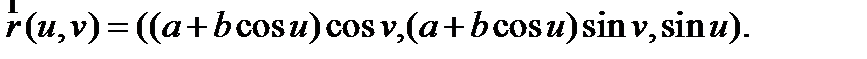
Рисунок 6 – Криволинейные координаты тора
Найдем координатные векторы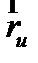 
и 
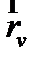по формуле (10):
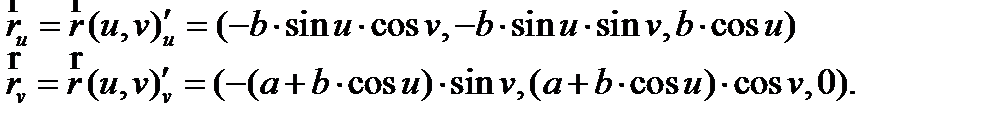
Далее найдем коэффициенты E , F , G первой квадратичной формы:
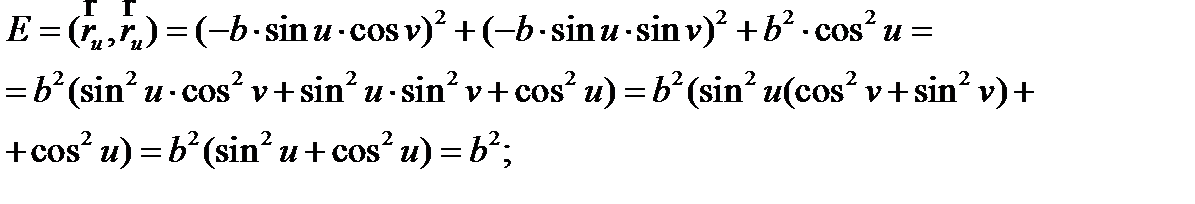
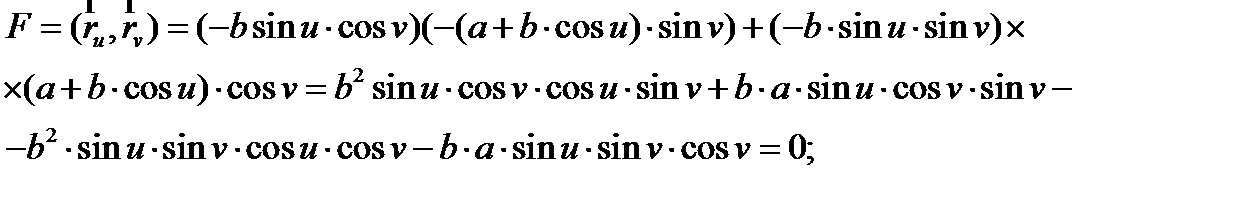
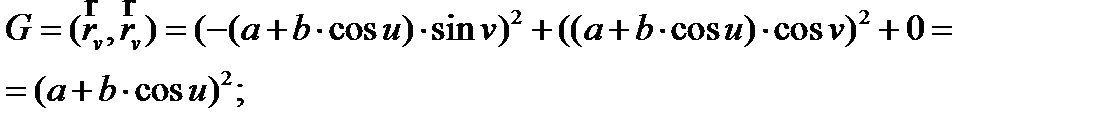
Таким образом, первая квадратичная форма будет выглядеть следующим образом:
Найдем координатные векторы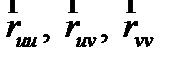 
по формуле (10):
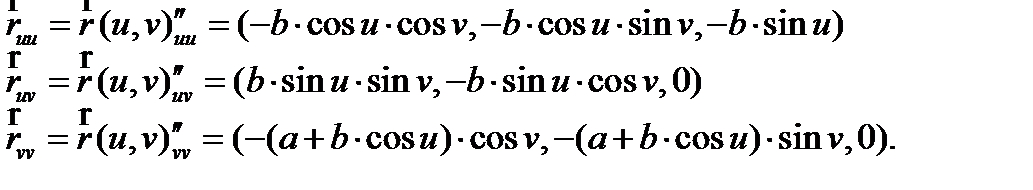
Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали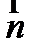 
:
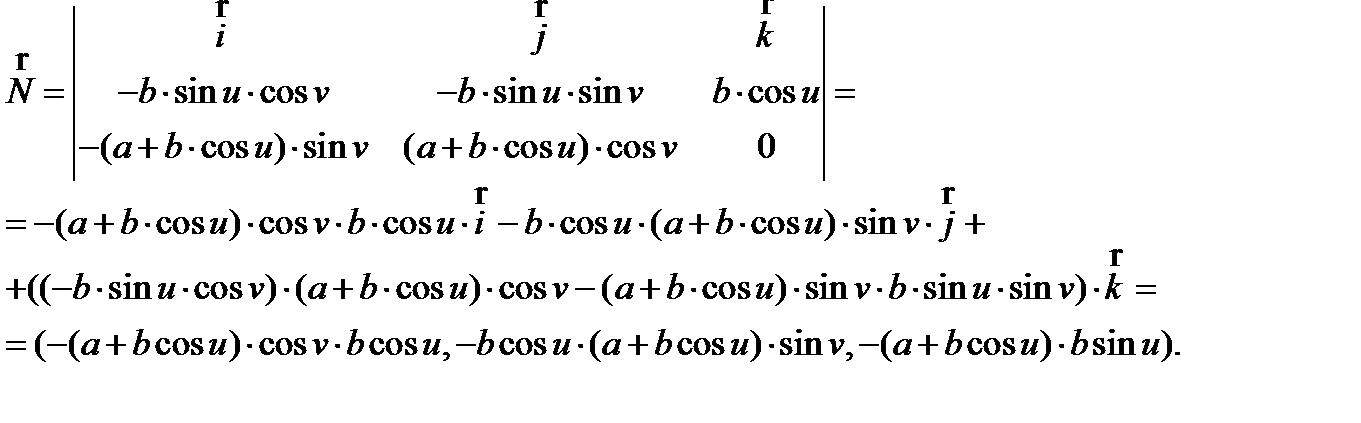
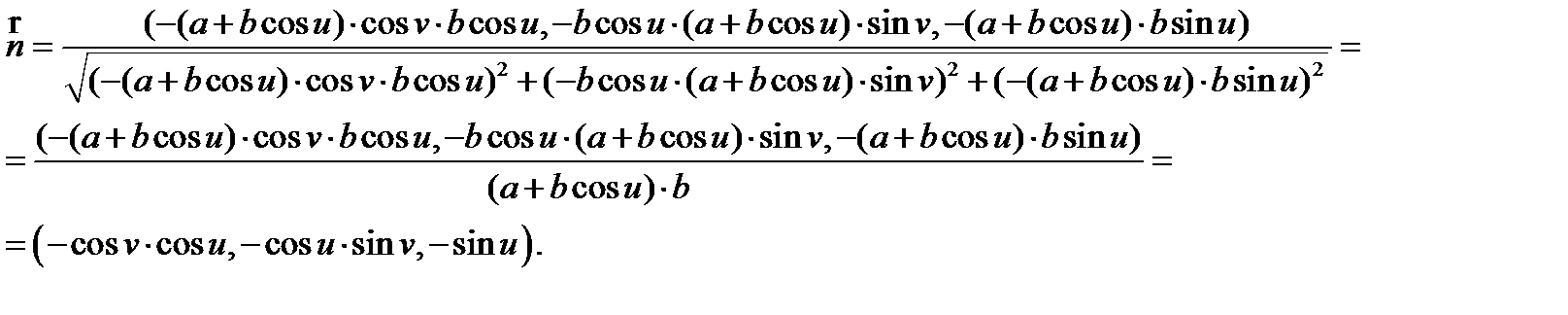Найдем коэффициенты L, M, N второй квадратичной формы:
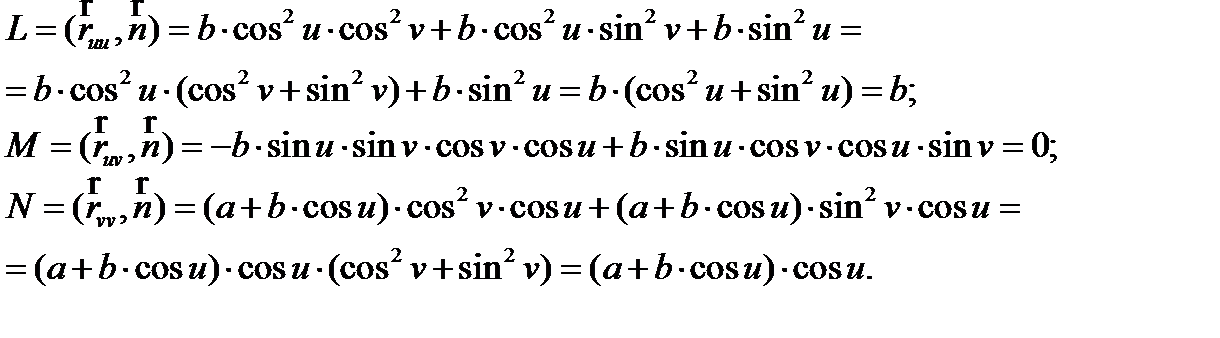
Таким образом, вторая квадратичная форма будет выглядеть следующим образом:
Найдем гауссову кривизну:
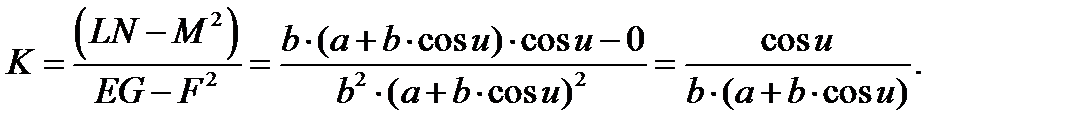
Найдем среднюю кривизну:
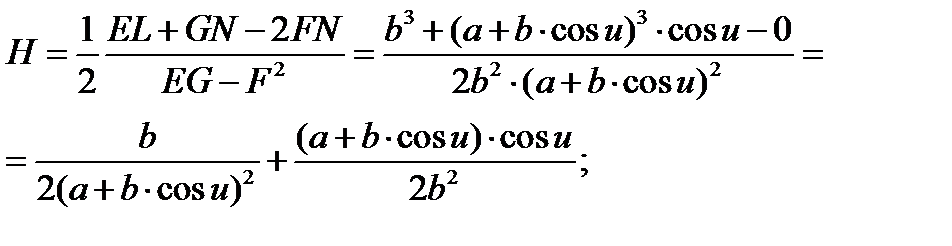
Таким образом, если сравнить матрицы первых квадратичных форм тора –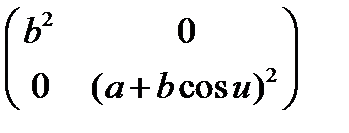 
и сферы – 
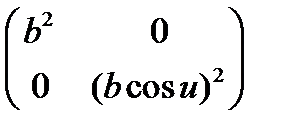, можно сделать вывод, что при a=0, матрица тора вырождается в матрицу сферы, т.е. сфера является частным случаем тора.
3.2 Геликоид
Геликоид – поверхность, образованная движением прямой, вращающейся вокруг оси и перпендикулярной к ней и одновременно поступательно движущейся в направлении этой оси, причем скорости этих движений пропорциональны. Параметризация Геликоида выглядит следующим образом (см. рис.7):
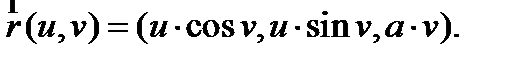
Рисунок 7 – Криволинейные координаты геликоида
Найдем координатные векторы 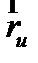и 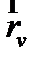по формуле (10):
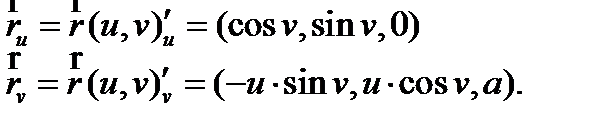
Далее найдем коэффициенты E , F , G первой квадратичной формы:
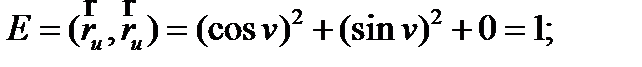
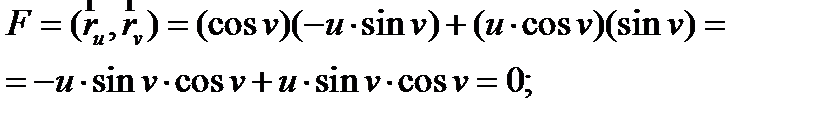
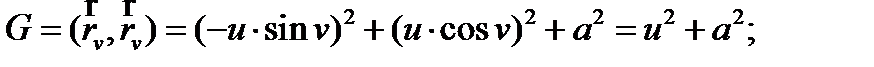
Таким образом, первая квадратичная форма будет выглядеть следующим образом:
Найдем координатные векторы 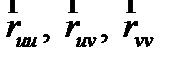по формуле (10):
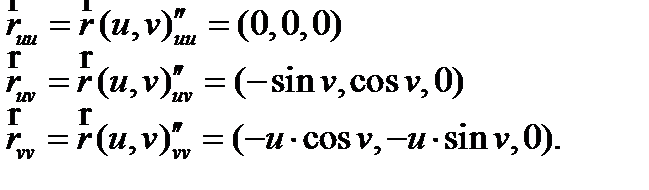
Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали :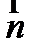
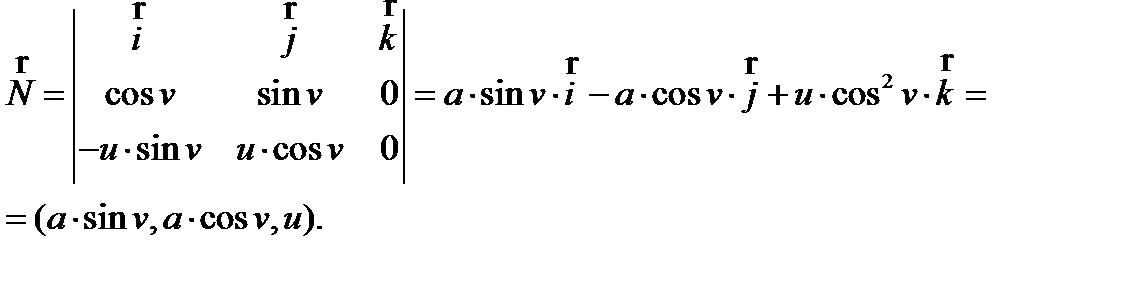
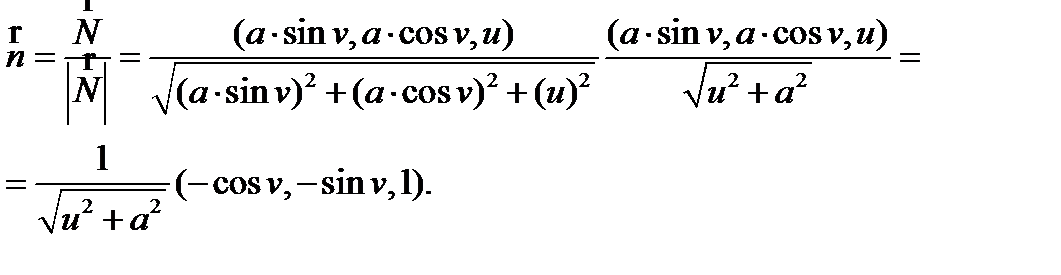
Найдем коэффициенты L, M, N второй квадратичной формы:
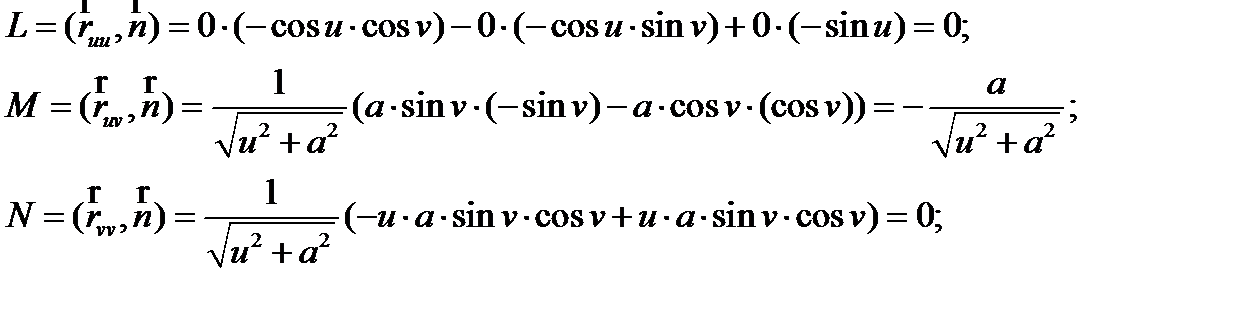
Таким образом, вторая квадратичная форма будет выглядеть следующим образом:
Найдем среднюю кривизну:
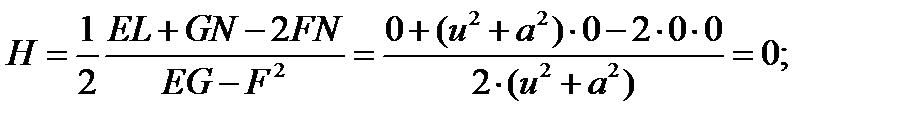
Найдем гауссову кривизну:
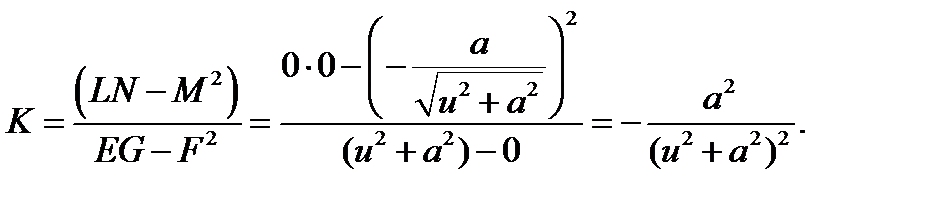
В данном случае гауссова кривизна отрицательна (K<0), поэтому поверхность является выпукло-вогнутой, что является верным утверждением по отношению к геликоиду, а средняя кривизна всегда равна 0.
ЗАКЛЮЧЕНИЕ
Таким образом, в ходе исследования элементов дифференциальной геометрии поверхностей, были выполнены следующие задачи:
· изучены все сведения из предметной области, которые были необходимы для решения задачи;
· проведен подробный анализ простых поверхностей – сферы, цилиндра, конуса; и более сложных – тора и геликоида;
· проведена параметризация поверхностей с помощью внутренних криволинейных координат, были найдены первая и вторая квадратичные формы поверхности, средняя и Гауссова кривизна;
· выявлено, что матрицы первой квадратичной формы сложных и простых поверхностей отличаются только элементами на главной диагонали матрицы, а элементы на побочной диагонали всех поверхностей – равны 0;
· подтверждены свойства гауссовой кривизны на конкретных примерах;
· найдена связь между сложной поверхности – тора, и простой поверхности – сферы, при помощи первой квадратичной формы;
· при работе со всеми формулами использовался математический редактор формул MathType 6;
· разработана программа визуализации поверхностей заданных параметрически, с помощью математической программы MATLAB [11].
Таким образом, цель данной курсовой работы была достигнута. В процессе изучения был получен опыт исследования некоторых характерных величин для поверхностей средствами дифференциальной геометрии.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Абрамов, А.В. Исследование свойств кривизны кривых и поверхностей в процессе изучения дифференциальной геометрии [Текст]: статья в сборнике трудов конференции – Н: Нижневартовский государственный университет, 2016. – 144-147 с.
2. Бермант, А.Ф. Краткий курс математического анализа [Текст]: учебник для вузов / А.Ф. Бермант, И.Г. Араманович. – 12-е изд. – СПб.: Лань, 2005. – 735 с.
3. Готман, А.Ш. Дифференциальная геометрия и её использование в проектировании обводов судов [Текст]: учебное пособие для вузов / А.Ш. Готман – Новосибирск: Новосиб. гос. акад. вод. трансп., 2011. – 44 с.
4. Демидович Б.П. Краткий курс высшей математики [Текст]: учебное пособие для вузов/ Б.П. Демидович, В.А. Кудрявцев. – М.: АСТ: Астрель, 2005. – 654 с.
5. Игнатьев, Ю.Г. Дифференциальная геометрия кривых и поверхностей в евклидовом пространстве [Текст]: учебное пособие для вузов. – Казань: Казанский университет, 2013. – 204 с
6. Лобкова Н.И. Высшая математика. Том 1 [Текст]: учебное пособие. – СПбГПУ: Издательство «Просвет», 2014. – 582 с.
7. Пискунов, Н. С. Дифференциальное и интегральное исчисления для вузов: Учеб. пособие для вузов [Текст] / Н.С. Пискунов. – 13-е изд. –М.: Наука, 1985. – 560 с.
8. Письменный, Д.Т. Конспект лекций по вышей математике: полный курс [Текст]: учеб. пособие для вузов / Д.Т. Письменный. – 4-е изд. – М.: Айрис-пресс, 2006. – 608 с.
9. Топоногов, В.А. Дифференциальная геометрия кривых и поверхностей [Текст]: учебное пособие для вузов/ В.А. Топоногов. – М.: Физматкнига, 2012. – 223 с.
10. Хорькова, Н.Г. Элементы дифференциальной геометрии и топологии поверхности в пространстве [Текст]: учеб. пособие для вузов / Н.Г. Хорькова. – М.: МГТУ им. Н.Э. Баумана, 2017. – 100 с.
11. MATLAB.Exponenta [Электронный ресурс] / Режим доступа: http://matlab.exponenta.ru/gui/book1/new7_3.php (Дата обращения: 05.05.18).
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ А
Листинг функции параметризации сферы
Рисунок А – параметризация сферы
clear ALL
clc;
a=1;
u=(0:0.05*pi:2*pi)';
v=[0:0.05*pi:2*pi];
X=a*cos(u)*cos(v);
Y=a*cos(u)*sin(v);
Z=a*sin(u)*ones(size(v));
figure('Color','w')
hS=mesh(X,Y,Z);
xlabel('x');ylabel('y');zlabel('z');
ПРИЛОЖЕНИЕ B
Листинг функции параметризации цилиндра
Рисунок В – параметризация цилиндра
clear ALL
clc;
a=3;
v=(-2:0.5:2)';
u=[0:0.05*pi:2*pi];
X=a*ones(size(v))*cos(u);
Y=a*ones(size(v))*sin(u);
Z=v*ones(size(u));
figure('Color','w')
hS=mesh(X,Y,Z);
xlabel('x');ylabel('y');zlabel('z');
ПРИЛОЖЕНИЕ C
Листинг функции параметризации конуса
Рисунок С – параметризация конуса
clear ALL
clc;
a=1;
u=(-2:1:0)';
v=[0:0.05*pi:2*pi];
X=u*cos(v);
Y=u*sin(v);
Z=u*ones(size(v));
figure('Color','w')
hS=mesh(X,Y,Z);
xlabel('x');ylabel('y');zlabel('z');