Глава I. Сведения из предметной области, необходимые для решения задачи
1.1 Криволинейные координаты и радиус вектор, параметризация поверхности
Пусть на поверхности задано некоторое семейство линий, зависящих от одного параметра. Семейство называется правильным [5] в некоторой области точек поверхности, если через каждую точку этой области проходит одна и только одна линия семейства.
Если на поверхности заданы два семейства линий, то они образуют сеть в той области, в которой оба семейства правильны, причем в этой области линии различных семейств пересекаются только в одной точке, не совпадают между собою и не касаются друг друга.
Пусть на поверхности задана сеть, удовлетворяющая всем этим условиям (см. рис.1). Линия одного семейства этой сети определяется значением параметра u, а линия другого семейства значением параметра v.
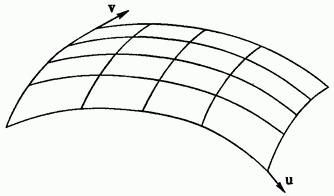
Рисунок 1 – Сеть на поверхности
Положение точки определит задание этих параметров, соответствующих кривым, пересекающимся в точке области. Так как через каждую точку области проходят определенные линии каждого семейства, то всякой фиксированной точке соответствуют определенные значения параметров u и v.
Криволинейные координаты [8] точки – это значения параметров u и v, определяющих кривые сети и пересекающиеся в данной точке поверхности. Эти линии и образованная ими сеть называются координатными линиями и координатной сетью. Вдоль одной координатной линии изменяется только одна криволинейная координата, а другая остается постоянной. На рисунке 2 приведен пример криволинейных координат на поверхности сферы.
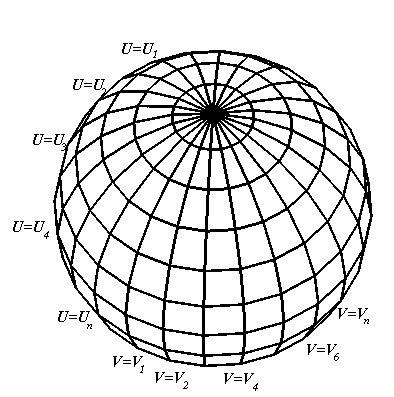
Рисунок 2 – Криволинейные координаты сферы
Если на поверхности введены криволинейные координаты, то говорят, что поверхность параметризована. Параметризация является наиболее удобным заданием поверхности. Задать поверхность параметризацией – значит задать поверхность, как график двумерной вектор-функции. Обозначим через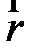 
радиус-вектор точки на поверхности, он определяется независимыми u , v, функция является функцией двух скалярных аргументов (u , v), т.е. 
.
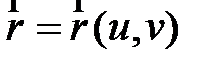Пусть поверхность задана параметрическим уравнением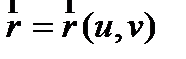 
, а принадлежащая ей кривая параметризована [2] с помощью параметра t. Таким образом, криволинейные координаты точек кривой, расположенных на поверхности являются функциями от t, т.е. каждому t соответствует (u , v)
( 
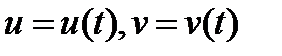). Параметризация кривой в трехмерном пространстве будет выглядеть следующим образом:
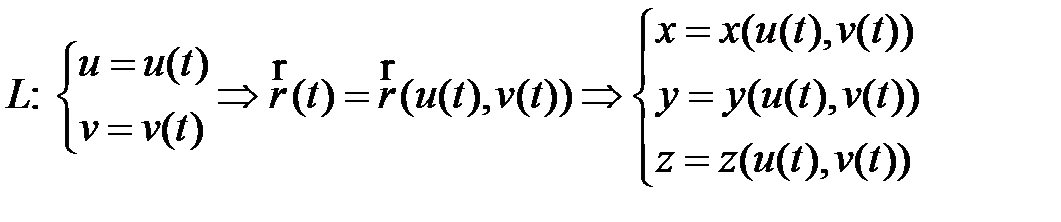(1)
Например, поверхности вращения [10] задаются следующим образом: пусть дана кривая, которая задана в плоскости xoz и будет вращаться вокруг оси oz:
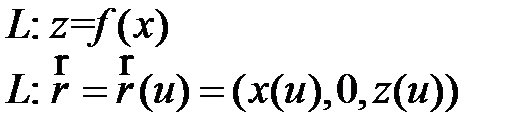(2)
Тогда поверхность будет задана:
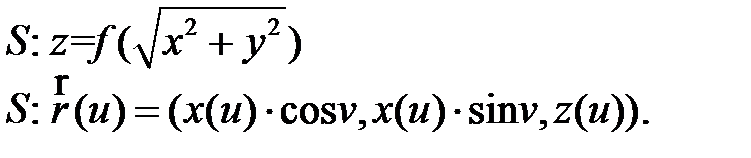(3)
1.2 Длина дуги, первая квадратичная форма
Вычислим длину дуги [3] L, заданной системой (1) на поверхности:
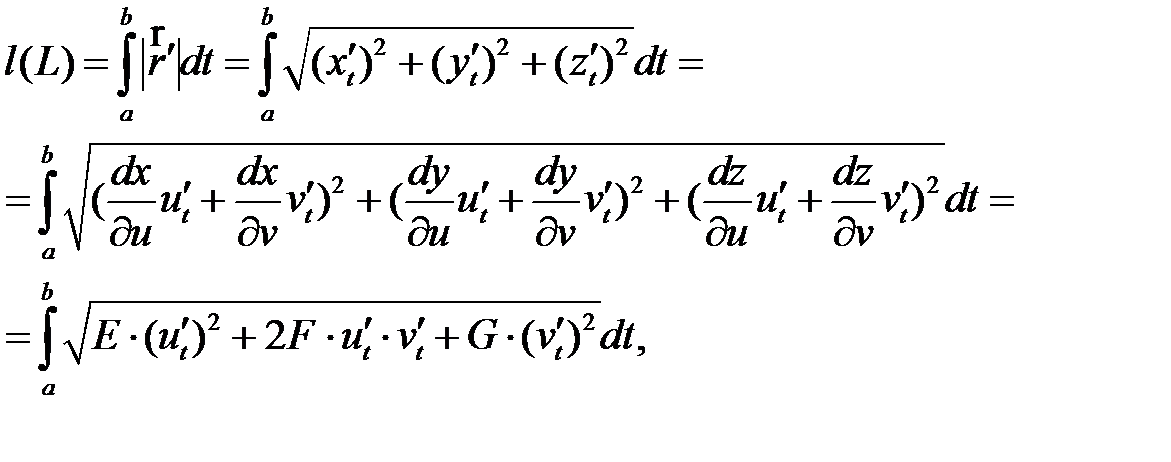(4)
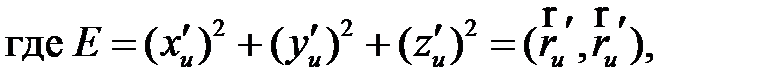
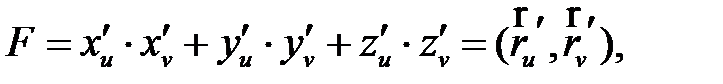
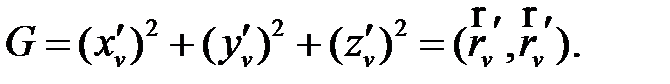
Здесь скобками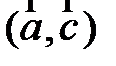 
обозначено скалярное произведение векторов. Далее для простоты будем записывать 
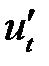, как 
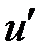, а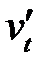 
– 
.
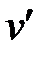В линейном пространстве квадратичная форма [6] – функция, которая вектору ставит в соответствие число. Предположим, что рассматривается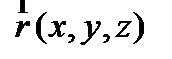 
. Тогда квадратичная форма – это функция Q, которую можно представить в следующем виде:
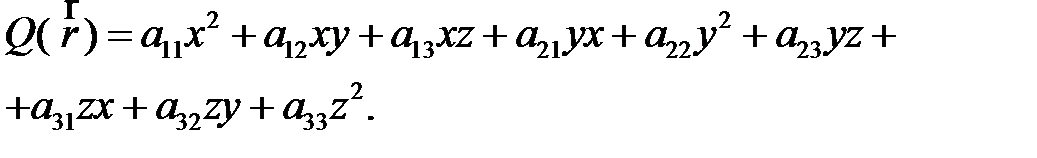(5)
Также квадратичную форму можно представить в матричном виде:
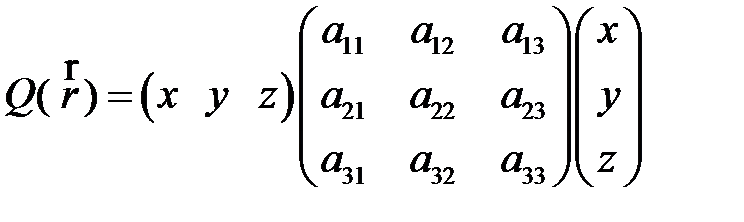(6)
Таким образом, смысл E, F, G – получить подкоренное выражение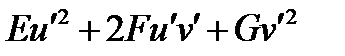 
в формуле (4), как матричное выражение:
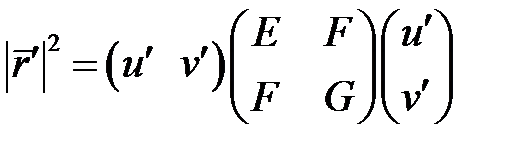(7)
где E , F , G – коэффициенты первой квадратичной формы,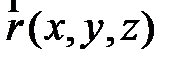 
.
Таким образом, первая квадратичная форма вычисляется по формуле:
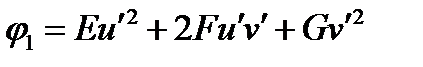(8)
Первая квадратичная форма играет основную роль во всей теории поверхностей. Т.o, если заданы E, F, G, u(t), v(t), то длину дуги можно вычислить даже если уравнение поверхности неизвестно.
1.3 Вторая квадратичная форма
Пусть дана поверхность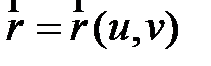 
. Тогда необходимо посмотреть соотношение с нормалью поверхности:
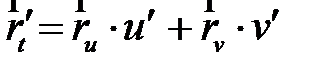(9)
При этом векторы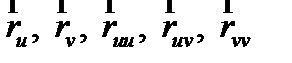 
, вычисляются следующим образом:
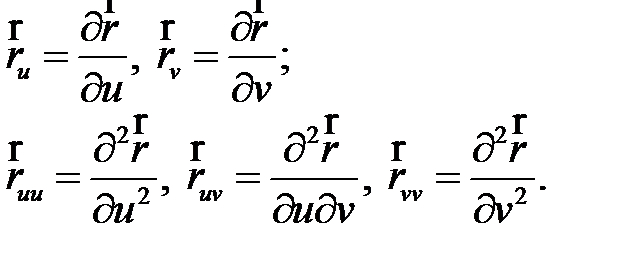(10)
Вторая производная радиус-вектора [4]:
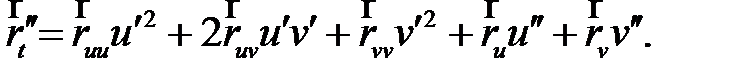(11)
Введем коэффициенты:
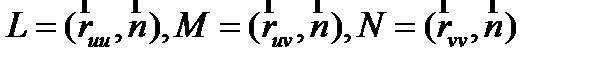(12)
где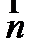 
– это единичный вектор нормали к поверхности.
Эти коэффициенты показывают, какую часть производных по касательному вектору в соответствующих направлениях составляет нормальная часть векторов.
Рассмотрим скалярное произведение проекции вектора от параметра на нормаль:
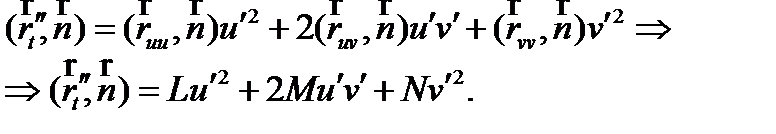(13)
Таким образом, вторая квадратичная форма вычисляется по формуле:
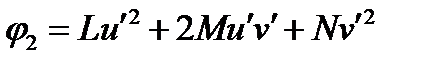(14)
Пусть у поверхности задана натуральная параметризация, а не произвольная (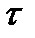 
– натуральный параметр, например, элемент длины):
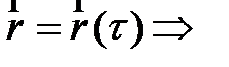по одному из уравнений Френе [9]:
Вторая производная радиус-вектора по натуральному параметру равна произведению кривизны кривой на нормаль к данной кривой.
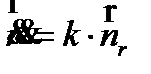(15)
где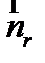 
– нормаль к кривой, k – кривизна кривой, точками 
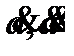обозначены соответственно первая и вторая производная по натуральному параметру.
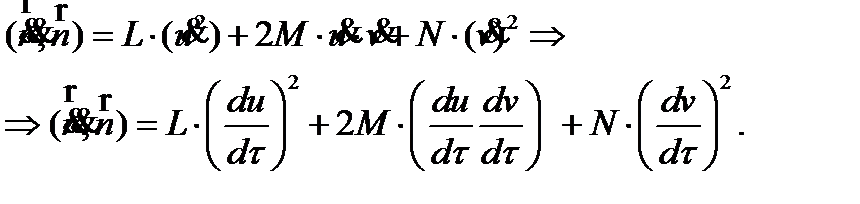(16)
Вспомним, что
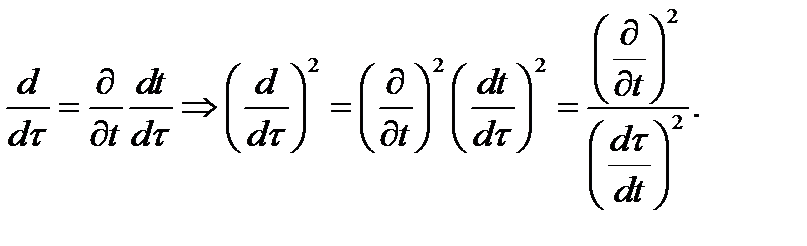(17)
Подставив формулу (17) в (16), снова переходим к параметру t и, учитывая, что – натуральный параметр длины, переобозначим его на l:
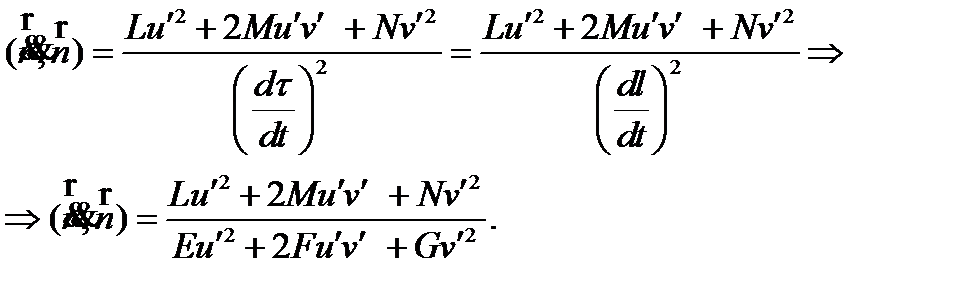(18)
Раскрывая скалярное произведение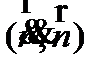 
и подставляя формулу (15), получим, что произведение кривизны на угол 
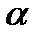между нормалью кривой и касательной к поверхности равно отношению второй и первой квадратичной форм:
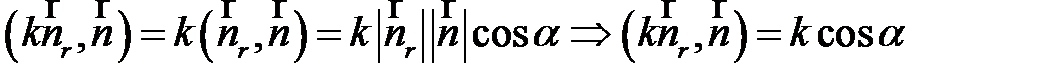
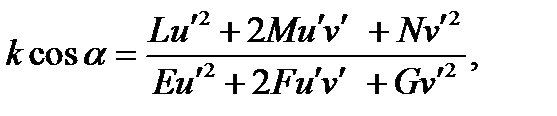(19)
где k – кривизна в точке поверхности.
1.4 Нормальные кривизны, гауссова кривизна
Для того, чтобы понять кривизну поверхности, наиболее удобным приемом является использование нормальных сечений поверхности. Тогда, нормальные кривизны [7] для нормальных сечений задаются функцией:
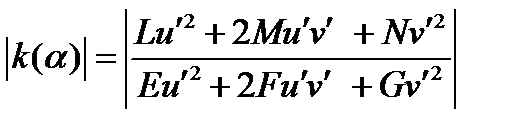. (20)
У функции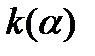 
есть два экстремальных значения:
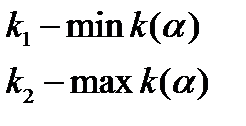(21)
где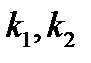 
– главные кривизны поверхности в точке.
Перемножив главные кривизны формулы (21), получим гауссову кривизну:
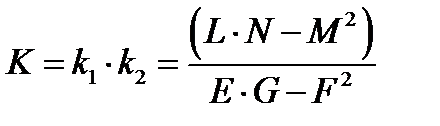. (22)
Гауссова кривизна имеет несколько замечательных свойств [1]:
· Если гауссова кривизна положительная (К>0), то поверхность является двояковыпуклой.
· Если гауссова кривизна нулевой кривизны (К=0), то поверхность является цилиндрической или конической.
· Если гауссова кривизна отрицательна (К<0), то поверхность является выпукло-вогнутой.
· не изменяется при изометрических изгибаниях.
Найдя среднее арифметическое главных кривизн формулы (21), получим среднюю кривизну:
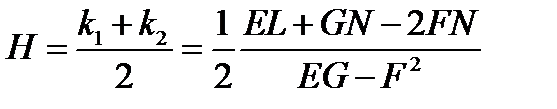. (23)
Таким образом, основными характерными элементами дифференциальной геометрии поверхностей являются: первая и вторая квадратичные формы поверхности, средняя и гауссова кривизна