8. Розрахункова швидкість повітря відносно штирів радіатора

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

МІНІСТЕРСТВО ОСВІТИ і НАУКИ, молоді та спорту УКРАЇНИ

ЧЕРНІВЕЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ІМЕНІ ЮРІЯ ФЕДЬКОВИЧА

Факультет комп’ютерних наук

Кафедра комп’ютерних систем та мереж

Заяц Роман

розрахунок Штирьового радіатора з Примусовою конвекцією

(Курсова робота)

Чернівці, 2012

Міністерство освіти і науки, молоді та спорту України

Чернівецький національний університет імені Юрія Федьковича

Факультет комп’ютерних наук

Кафедра комп’ютерних систем та мереж

ЗАТВЕРДЖУЮ

завідувач кафедри

доктор фіз.-мат. наук, проф.

________ С.В. Мельничук

„____” _________ 2012 р.

розрахунок Штирьового радіатора з Примусовою конвекцією

ЛИСТ ЗАТВЕРДЖЕННЯ

УЗГОДЖЕНО

Керівник проекту

канд. техн. наук

_________ А.П. Федоренко

„____” ________ 2012 р.

Виконавець

студент 2-го курсу

__________ Р.Р. Заяц

„____” ________ 2012 р.

2012

ЛЗ

ЗМІСТ

Вступ .......................................................................................... 4

1. Початкові дані ..................................................................5

2. Розрахунок теплових режимів радіатора ........5

Висновки ..................................................................................14

Список використаних джерел ....................................15

Додаток .....................................................................................16

Вступ

Дана курсова робота призначена для закріплення практичних навичок, отриманих при вивченні курсу „Основи конструювання обчислювальної техніки”.

Курсова робота виконуються згідно варіанту № 8.

Мета курсової роботи полягає у розрахунку теплових режимів роботи радіатора і виборі його типу, розрахунку температури радіатора та його геометричних розмірів, виконанні креслення радіатора.

1. Початкові дані

Дано:

Р = 10.5 Вт; R_ПК = 2.5 К/Вт; R_КР = 0.2 К/Вт; t_ПM = 90 °С; t_С = 25 °С; ε = 0.8; λ = 150 Вт/м∙К; υ = 1.0 м/с.

Тип радіатора – штирьовий, охолодження за допомогою примусової конвекції.

2. Розрахунок теплових режимів радіатора

1. Розглянемо рівняння (1)

t_П – t_C = (t_П – t_K) + (t_K – t_P) + (t_P – t_C).

З урахуванням того, що

θ_ПК = t_П – t_K = Φ∙R_ПК,

θ_КP = t_K – t_P = Φ∙R_КP,

рівняння (1) набуває вигляду

t_P = t_П – Φ (R_ПК + R_КP).

Згідно даним задачі, врахувавши, що Р = Φ, одержимо максимально допустиму температуру радіатора в місці кріплення НПП

t_P = 90 – 10.5 (2.5 + 0.2) = 61.65 °C.

2. Оскільки проектується штирьовий радіатор з примусовою конвекцією, то згідно рис. 7 задаємося наближеними значеннями θ_S = t_S - t_C та q = Φ/A. Даному типу радіатора відповідає зона а8-б8.

При перегріві θ_SC ≈ 40 °C будемо орієнтуватися на густину теплового потоку q = 3 · 10⁴ Вт/м². Оскільки Φ = 10.5 Вт, то орієнтовна площа основи радіатора

А= Φ/q = 10.5/3 · 10⁴ = 3.5· 10^{-4 м2}.

3. З конструктивних міркувань попередньо приймаємо, що форма основи радіатора квадрат (L × L = A), розмір L = 40 ∙ 10^{-3 м.}

Основа радіатора з однієї сторони має штирі, з іншої сторони кріпиться НПП. Штирьовий радіатор встановлюємо вертикально.

4. Згідно рис. 8б для штирьових радіаторів, що працюють в умовах примусової конвекції при кроці S_ш відповідають штрихові криві 5, 6, 8. Зупинимося на кривій 5. Згідно графіку при швидкості повітря υ = 1.0 м/с ефективне значення α_еф дорівнює приблизно α_еф = 250 Вт/м²К.

Згідно таблиці 2 зупинимось на таких розмірах:

висота штиря h = 20 мм = 2∙10^{-2 м;}

діаметр нижнього торця d₁ = 3 мм = 0.3∙10^{-2 м;}

діаметр верхнього торця d₂ = 1.2 мм = 0.12∙10^{-2 м;}

крок установки штирів S_Ш = 6 мм = 0.6∙10^{-2 м;}

5. Кількість штирів радіатора в одному ряду:

.

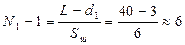Отже кількість штирів N₁ = 7 .

Оскільки основа радіатора квадратна, то рядів теж буде 7. Загальна кількість штирів N = 49.

6. Середньоповерхнева температура радіатора в першому наближенні

T_S = K_HP ∙ T_PMAX = 0.92 ∙ 61.65 = 56.72 °C.

де при примусовій конвекції штирьових радіаторів К_НР=0.94.

7. Сумарна площа перерізу каналів між ребрами

A_K = (N₁ - 1) ∙ (S_Ш – d₁) ∙ h = (7-1) ∙ (6 - 3) ∙ 10^-3 ∙ 2 ∙ 10^-2 = 0.36 ∙ 10^{-3 м2}.

8. Розрахункова швидкість повітря відносно штирів радіатора

υ_P = 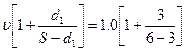= 2.0 м/с.

9. Задаємося декількома значеннями середньої температури основи радіатора t_P.

9.1. Нехай t_P = 50 °С.

Це відповідає перегріву θ_PC = t_P - t_S = 50 – 25 = 25 °C.

Тоді густина повітря при t_P = 50 °С згідно таблиці додатку Г

ρ_P = 1.093 кг/м³.

Питома теплоємність при цьому

С_Р = 1000 Дж/кг∙К.

Згідно формули (26) визначаємо середнє значення температури повітря в каналах між ребрами:

t_m = t_C + Φ_P/(2 ∙ υ_P ∙ A_K ∙ ρ ∙ С_Р) = 25+10.5/(2 ∙ 2.0 ∙ 0.36 ∙ 10^-3 ∙ 1.093∙10³) = = 31.67 °С.

Число Рейнольдса

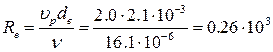
де ν – кінематична в’язкість при середній температурі t_m;

d_e – ефективний діаметр штиря

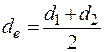= 2.1∙ 10^-3 м.

При примусовій конвекції, якщо

,

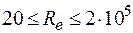то число Нуссельда визначається за формулою

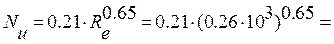
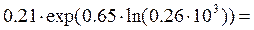= 7.8.

Коефіцієнт конвективної тепловіддачі

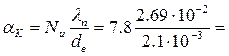99.92 Вт/м²К.

Визначаємо характеристичний параметр ребра

,

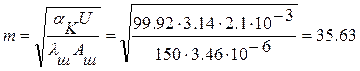де периметр поперечного перерізу штиря U = πd_e.

А_ш = 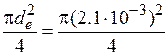= 3.46 · 10^{-6 м2}.

Тоді

,

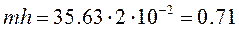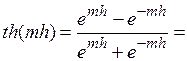0.71.

Згідно формули (14) конвективний тепловий потік

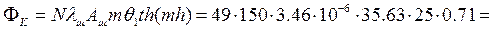16.08 Вт,

При вимушеній конвекції тепловіддачу через випромінювання можна знехтувати. Тому остаточно перегрів основи радіатора θ₁ = 25 °C забезпечує тепловий потік Φ₁ = 16.08 Вт.

9.2. Оскільки при перегріві θ₁ = 25 °C тепловий потік Φ₁ більше споживаної потужності Р = 10.5 Вт, то подальше збільшення перегріву для побудови теплової характеристики зупиняємо.

10. Будуємо теплову характеристику радіатора за двома точками (0, 0) та (25, 16.08)

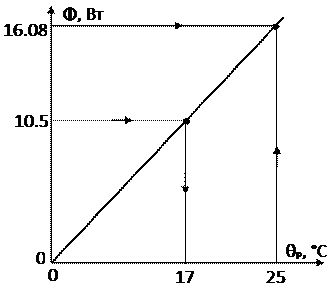Рис. 3.4. Теплова характеристика радіатора

11. Знаючи, що НПП споживає Р = 10.5 Вт за допомогою теплової характеристики знаходимо перегрів θ_Р=17 °С.

12. Температура радіатора в місці кріплення НПП

t_P = θ_Р + t_C = 17 + 25 = 42 °С.

Температура p - n переходу НПП

t_П = t_P + Φ(R_ПК+R_КР) = 42 + 10.5 (2.5+0.2) = 70.35 °С.

що менше допустимої температури t_ПМ=150 °С.

Отже радіатор задовольняє основній умові задачі. Потужність 10.5 Вт даний радіатор відводить при t_P =42 °С, t_П =70.35 °С.

3. З конструктивних міркувань попередньо приймаємо, що форма основи радіатора квадрат (L × L = A), розмір L = 31 ∙ 10^{-3 м.}

Основа радіатора з однієї сторони має штирі, з іншої сторони кріпиться НПП. Штирьовий радіатор встановлюємо вертикально.

4. Згідно рис. 8б для штирьових радіаторів, що працюють в умовах примусової конвекції при кроці S_ш відповідають штрихові криві 5, 6, 8. Зупинимося на кривій 5. Згідно графіку при швидкості повітря υ = 1.0 м/с ефективне значення α_еф дорівнює приблизно α_еф = 250 Вт/м²К.

Згідно таблиці 2 зупинимось на таких розмірах:

висота штиря h = 20 мм = 2∙10^{-2 м;}

діаметр нижнього торця d₁ = 3 мм = 0.3∙10^{-2 м;}

діаметр верхнього торця d₂ = 1.2 мм = 0.12∙10^{-2 м;}

крок установки штирів S_Ш = 6 мм = 0.6∙10^{-2 м;}

5. Кількість штирів радіатора в одному ряду:

.

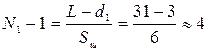Отже кількість штирів N₁ = 5.

Оскільки основа радіатора квадратна, то рядів теж буде 5. Загальна кількість штирів N = 25.

6. Середньоповерхнева температура радіатора в першому наближенні

T_S = K_HP ∙ T_PMAX = 0.92 ∙ 61.65 = 56.72 °C.

де при примусовій конвекції штирьових радіаторів К_НР=0.94.

7. Сумарна площа перерізу каналів між ребрами

A_K = (N₁ - 1) ∙ (S_Ш – d₁) ∙ h = (5-1) ∙ (6 - 3) ∙ 10^-3 ∙ 2 ∙ 10^-2 = =0.24 ∙ 10³ м².

8. Розрахункова швидкість повітря відносно штирів радіатора

U_P = 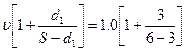= 2.0 м/с.