Глава 2. Построение модели и решение задачи определения оптимального плана производства в ООО «Мельник»
Фабрика ООО «Мельник» специализируется на выпуске двух сортов теста: бисквитное и песочное. Для изготовления теста используются такие ингредиенты как яйца и сахар, так же затрачивается и ресурсы труда. Для изготовления бисквитного теста требуется 5 штук яиц и 0,3 килограмма сахара, для изготовления затрачивается 15 минут. А для изготовления песочного теста потребуется 2 яйца, 0,25 килограмма сахара и 30 минут затраченного времени. Стоимость 1 кг бисквитного теста 30 руб., а песочного 20 руб. Общий запас яиц равен 1000 шт., 75 кг сахара и 125 часов трудовых ресурсов.
2.1. Построение экономико-математической модели
1. Переменные задачи.
В задаче требуется установить, сколько продукции каждого вида надо производить, поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида продукции:
х1 – суточный объем производства бисквитного теста, (кг);
х2 – суточный объем производства песочного теста, (кг).
2. Целевая функция.
В условии задачи сформулирована цель - добиться максимального дохода от реализации продукции, т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи продукции обоих видов, необходимо знать объемы производства, т.е. x1 и х2 кг продукции в сутки, а также цены на продукцию бисквитного и песочного теста - согласно условию 30 и 20 руб. за 1 кг продукции соответственно. Таким образом, доход от продажи суточного объема производства продукции бисквитного теста равен 30х1 руб. в сутки, а от продажи песочного теста - 20х2 тыс. руб. в сутки. Поэтому запишем целевую функцию в виде суммы дохода от продажи продукции бисквитного и песочного теста.
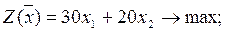 (руб.).
(руб.).
3. Ограничения.
Возможные объемы производства продукции х1 и х2 ограничиваются следующими условиями:
- количество яиц, сахара и трудовых ресурсов, израсходованных в течение суток на производство теста обоих видов, не может превышать запаса этих ингредиентов на складе;
- объем производства продукции не может быть выражен отрицательными значениями.
Запишем эти ограничения в математической форме.
Ограничение по расходу яиц имеет вид:
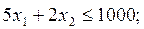 (т/сутки).
(т/сутки).
Левая часть ограничения - это расчет расхода яиц на производство теста обоих видов. Расход яиц на производство 1 кг бисквитного теста - 5 шт.; на производство 1 кг песочного теста - 2 шт. Тогда на производство х1 кг бисквитного теста и х2 кг песочного теста потребуется (5х1 + 2x2) шт. яиц. Правая часть ограничения - это величина запаса яиц на складе - 1000 шт.
Аналогична запись ограничения по расходу сахара:
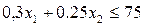 (кг).
(кг).
Так же ограничение по трудовым ресурсам имеет вид:
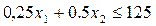 (чел.-ч.)
(чел.-ч.)
Неотрицательность объемов производства задается как
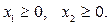
Таким образом, математическая модель задачи имеет вид:
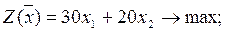 ;
;
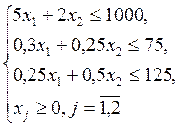
Экономико-математическая модель задачи состоит в том, чтобы найти такой план производства продукции 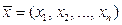 , удовлетворяющий системе ограничений, при котором целевая функция принимает максимальное значение.
, удовлетворяющий системе ограничений, при котором целевая функция принимает максимальное значение.
2.2. Определение оптимального плана производства симплексным методом
Приведем задачу к каноническому виду. Для этого в ограничения задачи введем дополнительные переменные х3, х4, х5 и перепишем условие задачи в виде уравнений:
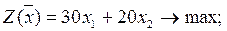
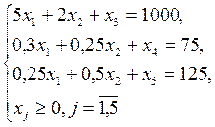
В качестве базисных переменных возьмем х3, х4, х5, тогда небазисные – х1, х2. Полагаем х1 = х2 = 0, тогда х3 =1000, х4=75, х5 =125.
1-я итерация.
Составляем первую симплексную таблицу, соответствующую исходному опорному решению (таблица 3):
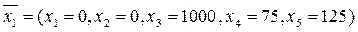
или
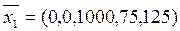
Таблица 3
| ci | БП | 30 | 20 | 0 | 0 | 0 | bi |
| x1 | x2 | x3 | x4 | x5 | |||
| 0 | x3 | 5 | 2 | 1 | 0 | 0 | 1000 |
| 0 | x4 | 0,3 | 0,25 | 0 | 1 | 0 | 75 |
| 0 | x5 | 0,25 | 0,5 | 0 | 0 | 1 | 125 |
| Dj | - 30 | - 20 | 0 | 0 | 0 | 0 | |
Все строки таблицы, за исключением индексной, заполняем по данным системы ограничений и целевой функции. Элементы последней строки рассчитываем:
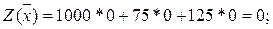
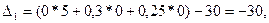
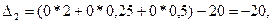
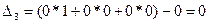 и т.д.
и т.д.
В индексной строке две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве разрешающего столбца следует принять столбец переменной х1:
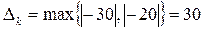 , т.е. k =1.
, т.е. k =1.
За разрешающую строку принимаем строку переменной х3:
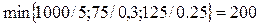 , т.е. s =1.
, т.е. s =1.
Разрешающим является элемент а11=5, т.е. вводим в базис переменную х1, выводим х3.
2-я итерация.
Формируем следующую симплексную таблицу (таблица 4)
Таблица 4
| ci | БП | 30 | 20 | 0 | 0 | 0 | bi |
| x1 | x2 | x3 | x4 | x5 | |||
| 30 | x1 | 1 | 0,4 | 0,2 | 0 | 0 | 200 |
| 0 | x4 | 0 | 0,13 | -0,06 | 1 | 0 | 15 |
| 0 | x5 | 0 | 0,4 | -0,05 | 0 | 1 | 75 |
| Dj | 0 | - 8 | 6 | 0 | 0 | 6000 | |
Из таблицы 4 находим опорный план:
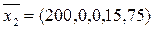 ,
, 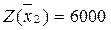
В индексной строке таблицы 4 имеется одна отрицательная оценка. Полученное решение можно улучшить. Разрешающим элементом является а22=0,13
3-я итерация.
Формируем следующую симплексную таблицу (таблица 5).
Таблица 5
| ci | БП | 30 | 20 | 0 | 0 | 0 | bi |
| x1 | x2 | x3 | x4 | x5 | |||
| 30 | x1 | 1 | 0 | 0,38 | -3,07 | 0 | 153,8 |
| 20 | x2 | 0 | 1 | -0,4 | 7,7 | 0 | 115,4 |
| 0 | x5 | 0 | 0 | 0,13 | -3,07 | 1 | 28,8 |
| Dj | 0 | 0 | 2,3 | 61,5 | 0 | 6923 | |
Из таблицы 5 находим опорный план:
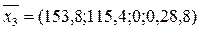 ,
, 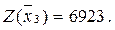
Так как все оценки свободных переменных положительные, найденное решение является оптимальным:
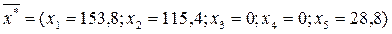
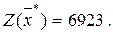
Максимальная прибыль составит 6923 рублей, при этом необходимо произвести 153,8 кг бисквитного теста и 115,4 кг песочного теста. В оптимальном плане ресурсы яиц и сахара равны нулю (х3=х4=0), так как они используются полностью. А резерв трудовых ресурсов х5 = 28,8, что свидетельствует о излишках.
Построение двойственной задачи
Оценки, приписываемые каждому виду ресурсов, должны быть такими, чтобы оценка всех используемых ресурсов была минимальной, а суммарная оценка ресурсов на производство единицы продукции каждого вида - не меньше цены единицы продукции данного вида.
Обозначим через y1 - двойственную оценку дефицитности яиц, через y2 –сахара, y3 – трудовых ресурсов. Тогда прямая и двойственная задачи формулируются:
прямая задача
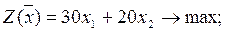
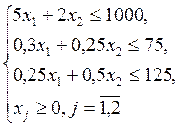
двойственная задача
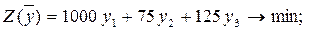
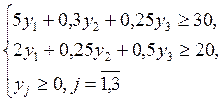
Решение прямой задачи дает оптимальный план производства песочного и бисквитного теста, а решение двойственной задачи - оптимальную систему оценок ресурсов, используемых для производства:
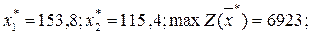
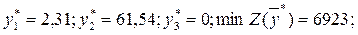
Двойственные оценки ресурсов yi* – это оценочные коэффициенты Dj дополнительных переменных х3, х4, х5 в последней симплексной таблице.
Исходя из анализа оптимальных двойственных оценок, можно сделать следующие выводы.
Ресурсы яиц и сахара используются полностью. Полному использованию этих ресурсов соответствуют полученные оптимальные оценки y1, y2, отличные от нуля. Значит, трудовые ресурсы недоиспользуются (х5 = 28,8 чел.-ч.).
2.3. Решение задачи оптимизации в табличном процессоре MS Excel
Для решения задач линейного программирования в MS Excel изначально мной был построен шаблон для ввода исходных данных
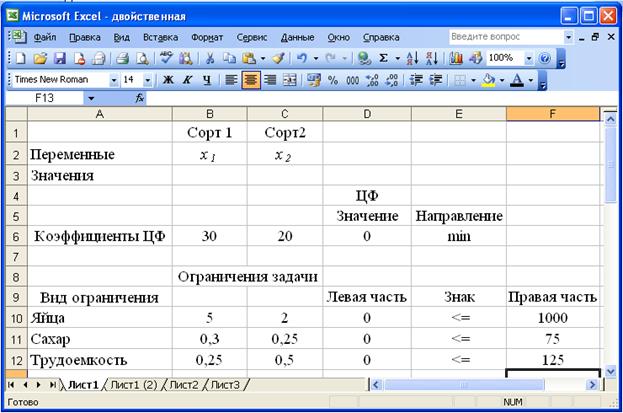
Рисунок 1 – Экранная форма задачи
Используя обозначения соответствующих ячеек в Excel, для расчета целевой функции была использована формула СУММПРОИЗВ, как сумма произведений соответствующих ячеек на соответствующие значения
Левые части ограничений задачи представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (таблица 7)
Таблица 7
| Левая часть ограничения | Формула Excel |
| 5x1+2x2 | =СУММПРОИЗВ($B$3:$C$3;B10:C10) |
| 0,3x+0,25x2 | =СУММПРОИЗВ($B$3:$C$3;B11:C11) |
| 0,25x1+0,5x2 | =СУММПРОИЗВ($B$3:$C$3;B12:C12) |
Далее оптимальный план для поставленной задачи нашла с помощью функции «Поиск решения»
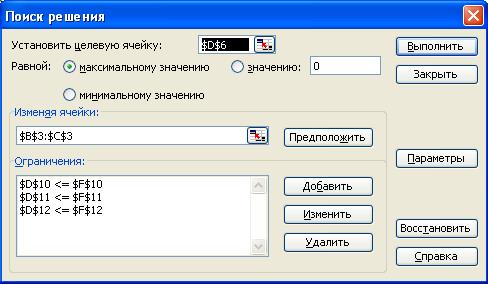
Рисунок 2 - Окно «Поиск решения» после ввода всех необходимых данных
В конечном итоге у нас получился оптимальный план решения задачи
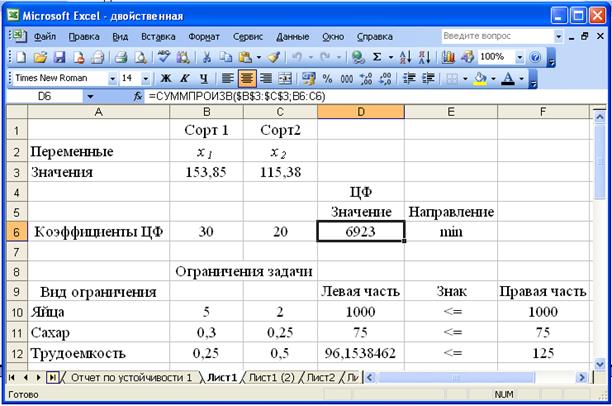
Рисунок 3 – Экранная форма после получения решения
Отчете по результатам (рис. 4). В этом отчете в столбцах «Результат» можно увидеть оптимальный план решения задачи: максимальную прибыль фабрики и производство двух сортов теста. А так же количество израсходованных ресурсов
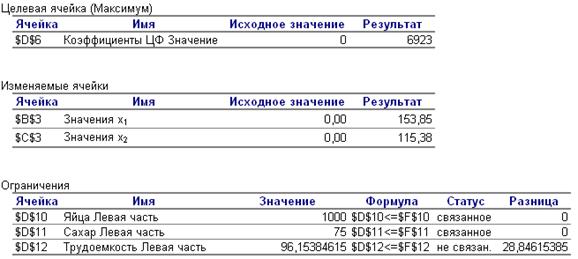
Рисунок 4 – Отчет по результатам
Отчет по устойчивости (рис. 5).В этом отчете можно увидеть оптимальное решение по производству теста. Так же допустимые приращения коэффициентов целевой функции, при которых сохраняется прежнее оптимальное решение и др
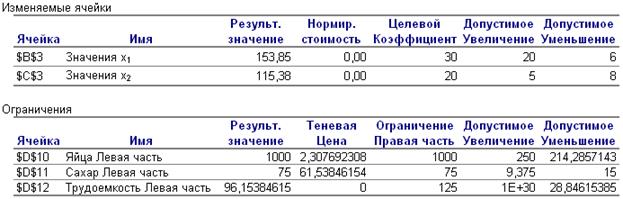
Рисунок 5 – Отчет по устойчивости
Отчет по пределам изменений представлен на рис. 6.
В отчете показано, в каких пределах может изменяться выпуск продукции, вошедший в оптимальное решение, при сохранении структуры оптимального решения. Там же даны соответствующие оптимальные значения целевой функции.
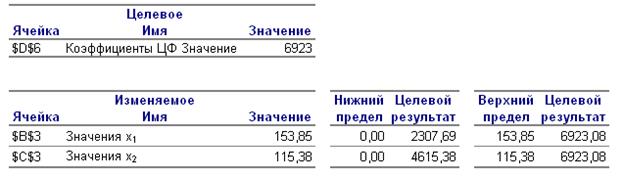
Рис. 6 – Отчет по пределам
Заключение
В ходе курсовой работы были решены следующие основные задачи построена экономико-математическая модель задачи, определен оптимальный план производства симплексным методом и решена задача оптимизации в табличном процессоре MS Excel.
Максимальная прибыль фабрики по изготовлению теста составила 6923 рублей, при этом необходимо произвести 153,8 кг бисквитного теста и 115,4 кг песочного теста.
Исходя из анализа оптимальных двойственных оценок, можно сделать следующие выводы:
Запасы яиц и сахара используются полностью. Полному использованию этих ресурсов соответствуют полученные оптимальные оценки y1, y2, отличные от нуля. Значит, трудовые ресурсы недоиспользуются в размере 28,8 чел.-ч.
Увеличение количества яиц на 1 шт. приведет к тому, что появится возможность найти новый оптимальный план производства продукции, при котором общая прибыль возрастает на 2,31 руб. и станет равной 6923 + 2,31 = 6925,31 руб. Анализ полученных оптимальных значений новой прямой задачи показывает, что это увеличение общей прибыли достигается за счет увеличения производства бисквитного теста на 0,38 руб. и сокращения выпуска бисквитного теста на 0,4 руб. Вследствие этого использование трудовых ресурсов увеличится на 0,13 руб.
Точно так же увеличение на 1 кг. количества сахара позволит перейти к новому оптимальному плану производства, при котором прибыль возрастет на 61,54 руб. и составит 6984,5 руб., что достигается за счет уменьшения выпуска бисквитного теста на 3,07 руб. и увеличения выпуска песочного теста на 7,7 руб., причем объем используемых трудовых ресурсов увеличится на 3,07 руб.
Уменьшение количество запасов сахара на 15 кг приведет к тому что появится новый оптимальный план производства при котором общая прибыль уменьшится на 923 рубля, т.е. станет равен 6000 рублей.
Увеличение цены бисквитного теста с 30 до 40 рублей за 1 кг не изменит оптимальное решение, т.к при анализе в отчете по устойчивости «Допустимое увеличение» равно 20, а это значит что при увеличении цены до 50 рублей за кг оптимальное решение не будет изменено.
Список использованной литературы
1. Акулич И.Л. Математическое программирование в примерах и задачах. М., 2007.
2. Грешилов А.А. Прикладные задачи математического программирования. М., 2009.
3. Конюховский П.В. Математические методы исследования операций в экономике. - СПб: Питер, 2010
4. Хемди А. Таха. Введение в исследование операций. 7-е изд. — М.: «Вильямс», 2007.
5. Электронный учебник. Математические методы. © 2008 ВТК
Автор: Попова Н.В. Разработчик: Родионова И.В. http://matmetod-popova.narod.ru/








