Таким образом, группа , состоящая из двух подвижных звеньев и трех кинематических пар пятого класса и не распадается на более простые кинематические цепи является базовой и называется группой Ассура.
Группы делят на классы в зависимости от класса контура, в качестве которого принимают замкнутую область части плоскости, занятой звеном или ограниченной со всех сторон звеньями.
Класс контура определяется числом внутренних кинематических пар, входящих в этот контур.
Класс группы определяют наивысшим классом, входящего в его состав.
Наиболее распространенными являются группы второго класса, которые разделяют на пять видов. Вид группы второго класса определяется в зависимости от числа и относительного расположения поступательных и вращательных кинематических пар в ней.
Класс механизма устанавливают по наивысшему классу группы, входящей в состав данного механизма.
Для определения класса механизма необходимо выделить из него группы, начиная с наиболее удаленных от ведущего звена, в результате чего остается механизм первого класса.
Выделение группы производится при одновременной проверке оставшейся части механизма после выделения соответствующих групп.
Это исследование называется структурным анализом механизма.
Порядок проведения структурного анализа: определяется количество кинематических звеньев и кинематических пар; исключаются звенья, носящие лишние степени свободы; производится замена высших кинематических пар цепями с низшими парами; выделяются структурные группы; определяется класс механизма.
Структурные признаки механизма характеризуют его составные части и связи между ними, что отражается структурной схемой.
Схема механизма представляет собой его графическое изображение, выполненное с использованием условных обозначений, рекомендованных нормативными регламентами и содержащая информацию о составе и расположению элементов механизма, отражающая структурные признаки механизма, характеризующая его составные части и связи между ними. В случае, когда на схеме не указаны геометрические и кинематические параметры, она называется структурной.
На рисунке 1.2 представлена структурная схема кривошипно – ползунного механизма (КПМ).
При построении схемы с соблюдением конкретных характеристик и пропорций схема называется кинематической.
Основными метрическими характеристиками КПМ являются: длина кривошипа l 1 = l ОА; длина шатуна l 2 = l АВ; смещение (эксцентриситет) направляющих ползуна е, соотношение которых между собой определяет входные параметры при синтезе механизма l ( l= l 1/ l 2) и e (e= е/ l 1).
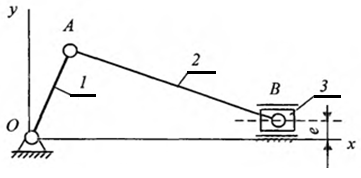
Рисунок 1.2 – Структурная схема кривошипно – ползунного механизма:
1 – кривошип; 2 – шатун; 3 – ползун.
При построении схемы с соблюдением конкретных характеристик и пропорций схема называется кинематической.
Основными метрическими характеристиками КПМ являются: длина кривошипа l 1 = l ОА; длина шатуна l 2 = l АВ; смещение (эксцентриситет) направляющих ползуна е, соотношение которых между собой определяет входные параметры при синтезе механизма l ( l= l 1/ l 2) и e (e= е/ l 1).
Полный ход ползуна Н (рисунок 1.3) устанавливают при нахождении ползуна в крайних положениях, когда кривошип ОА и шатун АВ складываются или вытягиваются в одну линию.
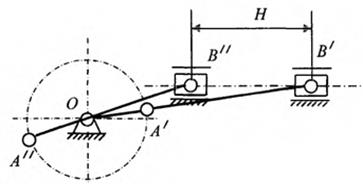
Рисунок 1.3 – Схема КПМ в крайних положениях: ОВ ¢ – крайнее дальнее
положение ( l 1 + l 2 ); ОВ ¢ ¢ – крайнее ближнее положение ( l 2 – l 1 );
Основные размеры схемы механизма устанавливают метрическим синтезом. При этом выбор оптимального варианта кинематической схемы построен на основных условиях геометрии, кинематики, динамики и технологичности, которые отражаются: проворачиваемостью кривошипа; системой передачи сил звеньями механизма; отношением времени прямого и обратного ходов механизма; ходом ведомого звена; закономерностями изменения скоростей и др.
Условие проворачиваемости заключается в том, что должна обеспечиваться возможность непрерывного перехода звена из одного заданного положения в другое, поскольку между двумя заданными положениями может оказаться промежуточное, в котором движение звеньев невозможно ( l 1 + е < l 2).








