Степень подвижности пространственных механизмов определяется по формуле Сомова-Малышева
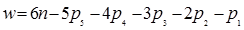 . (1.5)
. (1.5)
В формулах (1.4), (1.5): n – число подвижных звеньев; p 5 – число кинематических пар пятого класса; p4 – число кинематических пар четвертого класса; p 3 – число кинематических пар третьего класса; p 2 – число кинематических пар второго класса; p 1 – число кинематических пар первого класса.
Число степеней свободы механизма равно числу независимых вариаций обобщенных координат. При w =1обобщенная координата приписывается начальной кинематической паре (начальному двухзвеннику. Рисунок 1.1).
В этом случае одно из звеньев начальной пары является стойкой, а второе звено называют начальным звеном.
Поскольку обобщенные координаты приписываются начальному двухзвеннику или начальному звено, то совокупность остальных звеньев механизма должна обладать нулевой подвижностью.
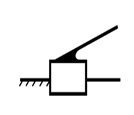
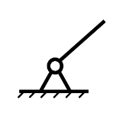
а) б)
Рисунок 1.1 – Начальный механизм: а) – с вращательной кинематической парой;
б) – с поступательной кинематической парой
Степень подвижности механизма свидетельствует о количестве ведущих звеньев в нём.
Механизмы классифицируются: по характеру движения – плоские и пространственные; по видам кинематических пар – механизмы с высшими и низшими кинематическими парами; по назначению; по принципу передачи усилий; по конструктивному признаку.
Для плоских шарнирных механизмов с парами пятого класса распространение получила классификация, предложенная Л.В. Ассуром и И.И. Артоболевским. Структурными признаками, в этом случае, являются признаки, которые характеризуют возможность выделение отдельных групп звеньев и их соединений.
Согласно этой классификации механизмы объединяют в классы от первого и выше. Механизм первого класса состоит из ведущего звена и стойки, соединенных кинематической парой пятого класса; механизмы более высоких классов образуются последовательным присоединением к механизму первого класса кинематических цепей, не изменяющих степени подвижности исходного механизма, т.е. имеющим степень подвижности, равную нулю.
Кинематическая цепь, которая будучи присоединенной свободными элементами пар (внешние пары) к стойке, обладает нулевой степенью подвижностью, называется группой.
В случае, когда в состав группы входят только группы пятого класса (пары четвертого класса условно заменены цепями с парами пятого класса) степень подвижности равна
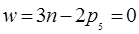 . (1.6)
. (1.6)
Тогда количество пар пятого класса равно
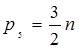 (1.7)
(1.7)








