.Логический элемент «И» - конъюнкция, логическое умножение, AND
1. Операции и теоремы Булевой алгебры
Основными операциями булевой алгебры являются операции логического сложения, умножения и отрицания.
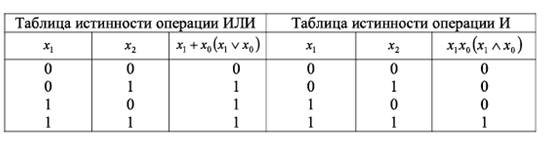
Логическое сложение. Операция ИЛИ или дизъюнкцией. Она
соответствует математической операции объединения множеств.
Логическое умножение. Операция И или конъюнкцией. Она
соответствует математической операции пересечения множеств.
Отрицание. Инверсия или дополнение. Для ее обозначения используют черту над соответствующим выражением. Операция определяется постулатами:
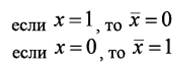
Теоремы булевой алгебры отражают связи, существующие между операциями, выполняемыми над логическими переменными.
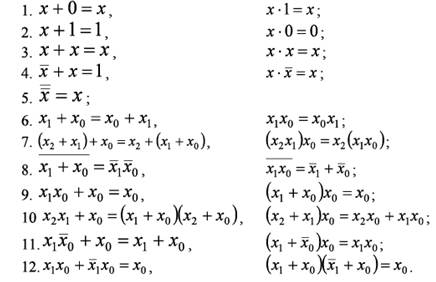
2. Логические элементы. Обозначение. Логические операции. Таблица истинности.
В соответствии с перечнем логических операций различают три
основных логических элемента (ЛЭ): И, ИЛИ, НЕ.
.Логический элемент «И» - конъюнкция, логическое умножение, AND
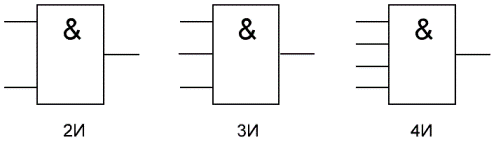
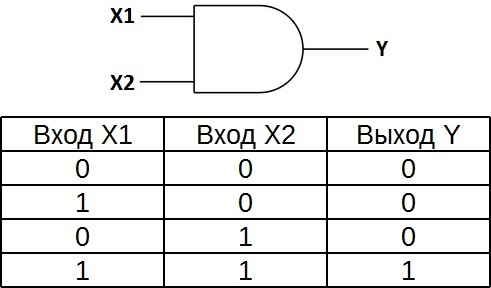
«И» - логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Логический элемент «ИЛИ» - дизъюнкция, логическое сложение, OR
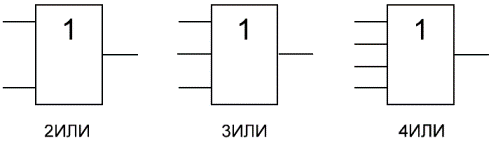
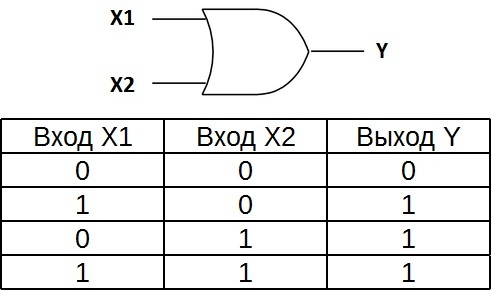
«ИЛИ» - логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
Логический элемент «НЕ» - отрицание, инвертор, NOT
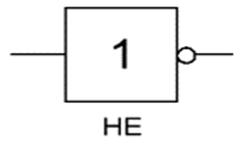
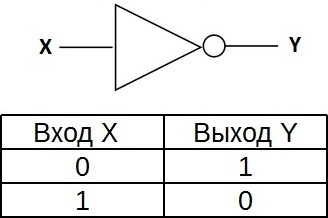
«НЕ» - логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».
3. Синтез комбинированных цепей. Диаграмма Вейча
Этапы синтеза: 1. Составляется таблица функционирования логической цепи - таблица истинности. Эта таблица показывает, чему равен выходной сигнал цепи при различных сочетаниях входных сигналов; 2. Исходя из таблицы истинности записывается логическая функция; 3. Логическая функция минимизируется и преобразуется к виду, удобному для реализации на логических ячейках заданного типа
Пусть необходимо построить мажоритарную ячейку на три входа, т. е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно единиц.
Таблица истинности
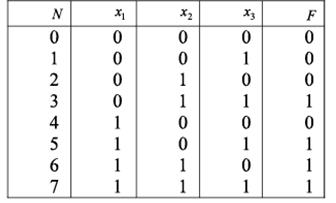
Логическая функция
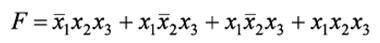
Минимизация:
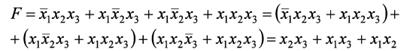
Для элементов И-НЕ:
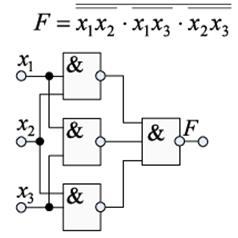
Диаграмма Вейча прямоугольная таблица, в которой число клеток равно числу возможных минтермов. Каждой клетке таблицы ставится в соответствие определенная конъюнкция, причем делается это таким образом, чтобы в соседних клетках (снизу и сверху, слева и справа) конъюнкции отличались не более чем одним сомножителем. При заполнении таблицы в соответствующую клетку ставится 1, если минимизируемая функция при данном наборе аргументов равна единице. В остальные клетки таблицы вписываются нули.
Правила проведения контуров: контур должен быть прямоугольным; внутри контура должны быть только клетки, заполненные единицами; число клеток, находящихся внутри контура, должно быть целой степенью числа 2, т.е. может быть равно 1, 2, 4, 8...; одни и те же клетки, заполненные единицами, могут входить в несколько контуров; при проведении контуров самая нижняя и самая верхняя строки таблицы считаются соседними, то же - для крайнего левого и крайнего правого столбцов; число контуров должно быть как можно меньшим, а сами контуры как можно большими.
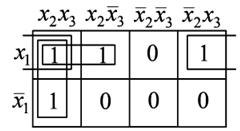
При проведение контуров, охватывающий единицы первый и четвертый столбцы считаются соседними, диаграмму можно представить себе как бы свернутой в виде цилиндра. Для того чтобы найти логическое выражение, которое описывает в диаграмме Вейча контур, охватывающий единицы, нужно рассмотреть обозначения строк и столбцов, входящих в этот контур, и исключить из этих обозначений те аргументы, которые изменяют свое значение внутри контура. Если, например, контур охватывает столбцы х2х3и х2х3, то аргумент х3 из обозначения контура следует исключить. Учитывая, что этот контур располагается в строке x1 получаем окончательное обозначение контура x1x2 Выписывая, таким образом, обозначения всех трех контуров, находим выражение, уже полученное нами ранее алгебраическим путем:
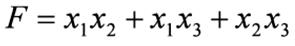
4. Мультиплексоры и демультиплексоры. Назначение, обозначение, принцип действия
Мультиплексором называется комбинационное логическое устройство, предназначенное для управляемой передачи данных от нескольких источников информации в один выходной канал.
Применение: передача информации от нескольких разнесенных в пространстве источников (датчиков) информации на вход одного приемника.
Принцип действия:
Мультиплексор имеет один выход и две группы входов: информационные и адресные. Код, подаваемый на адресные входы, определяет, какой из информационных входов в данный момент подключен к выходному выводу. Поскольку n - разрядный двоичный код может принимать 2n значений, то, если число адресных входов мультиплексора равно n, число его информационных входов должно равняться 2n
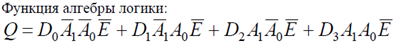
Условное графическое обозначение :
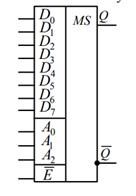
Демультиплексор – комбинационное логическое устройство, предназначенное для управляемой передачи данных от одного источника информации в несколько выходных каналов.
Демультиплексор имеет один информационный вход, n адресных входов и 2n выходов.
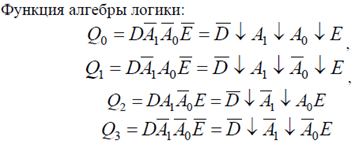
Демультиплексор принимает одну единственную линию ввода данных, а затем переключает его в любой из ряда отдельных выходных линий по одному за раз. Он преобразует последовательный сигнал данных на входе до параллельных данных на своих выходных линиях.
Условное графическое обозначение :
5. Шифраторы и дешифраторы. Назначение, обозначение , принцип действия
Шифратором (кодером) называется комбинационное логическое устройство для преобразования чисел из десятичной системы счисления в двоичную.
Входам шифратора последовательно присваиваются значения десятичных чисел, поэтому подача активного логического сигнала на один из входов воспринимается шифратором как подача соответствующего десятичного числа. Этот сигнал преобразуется на выходе шифратора в двоичный код. Если шифратор имеет п выходов, число его входов должно быть не более чем 2n. Шифратор, имеющий 2n входов и п выходов, называется полным. Если число входов шифратора меньше 2n он называется неполным.
Пример: Шифратор - преобразователь десятичных чисел от 0 до 9 в двоично-десятичный код. Число входов данного устройства меньше 2n =16, имеем неполный шифратор.
Можно записать следующие выражения:
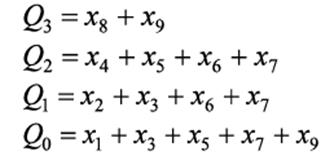
Полученная система ФАЛ характеризует работу шифратора.
Логическая схема устройства:
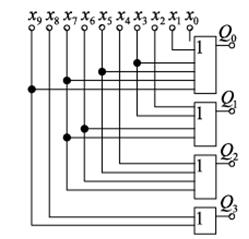
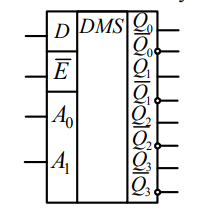
Дешифратором (декодером) называется комбинационное логическое устройство для преобразования чисел из двоичной системы счисления в десятичную.
Дешифратор выполняет операцию, обратную шифратору. Если число адресных входов дешифратора п связана с числом его выходов т соотношением т = 2n , то дешифратор называют полным. В противном случае, т. е. если т < 2n , дешифратор называют неполным.
Поведение дешифратора описывается системой уравнений.
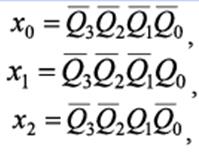
и так далее, где Q1, — значение логической переменной на i-м входе устройства.
В общем виде эта система имеет вид Х1 = (Q3 Q2 Q1 Q0 )
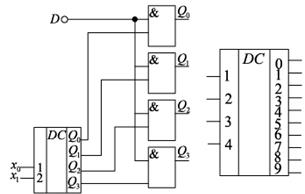
6.RS-триггеры. Назначение, обозначение, принцип действия
Асинхронный RS-триггер - элемент памяти, который реализован на элементах И-НЕ или ИЛИ-НЕ, снабжен только двумя информационными
входами: входом сброса R и входом установки S.
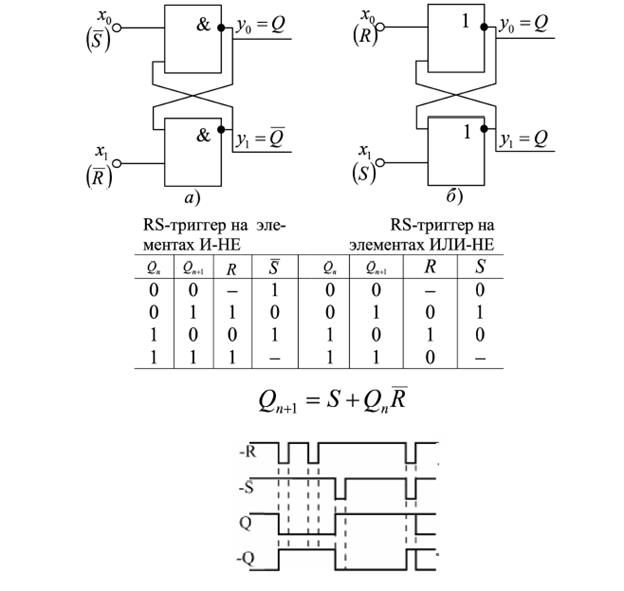
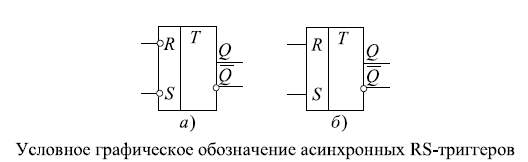
Синхронный RS - триггер выполнен на основе асинхронного RS-триггера, введением дополнительной логической схемы, которая формирует на его входах активные логические уровни только при наличии дополнительного сигнала синхронизации.
7. D -тригерры. Назначение, обозначение, принцип действия
D - триггер -меняет свое состояние по изменению сигнала С в зависимости от состояния входа данных D.
Таблица истинности D-триггеров
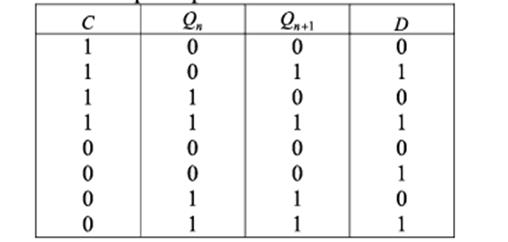
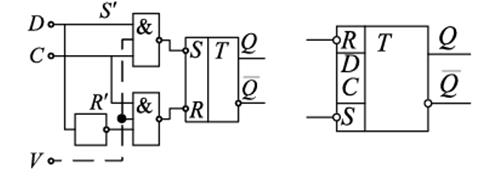
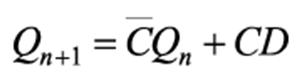
Разновидностью D-триггера является VD — триггер. Этот триггер дополнительно снабжен входом разрешения работы V, который блокирует его работу. При V = 1 поведение триггера полностью соответствует выражению (1). При V = 0 триггер хранит записанную ранее в него информацию: Qn+1 = Qn .
D-триггер также может быть снабжен дополнительными входами асинхронной установки.
ФАЛ D — триггера имеет вид
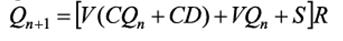
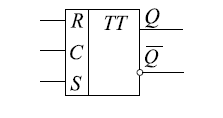
8.T-триггеры. Назначение, обозначение, принцип действия.
Т - триггер ( счетный триггер) изменяет свое состояние на противоположное о каждому активному логическому сигналу, действующему на информационном входе Т.
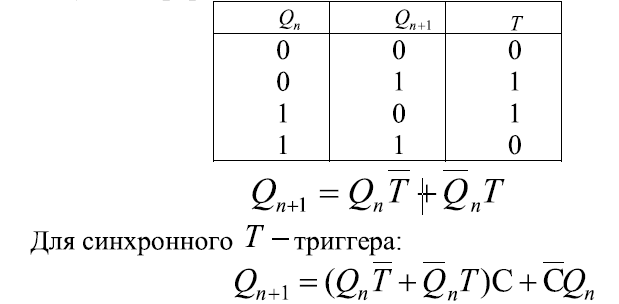
Реализация данного режима работы с использованием простейшего элемента памяти требует подачи на последний для каждого последующего переключения инверсных значений входных сигналов. Такой режим обеспечивается введением второго запоминающего элемента. При этом новая информация формируется сначала только во входной ступени триггера при сохранении старой информации в выходной его ступени. Когда новое стояние входной ступени сформировано и снят активный уровень сигнала со входа Т, происходит ее перезапись в выходную ступень устройства. Таким образом, двухступенчатым триггер состоит из двух последовательно соединенных триггеров - ведущего и ведомого.
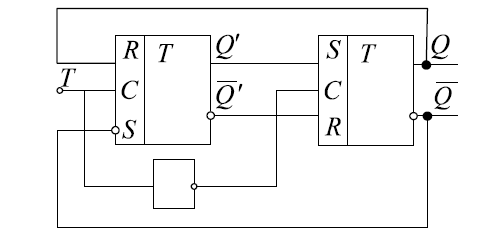
Для устранения режима автоколебаний синхронизация работы ведущего и ведомого триггеров осуществляется инверсными логическими уровнями.
На принципиальных схемах двухступенчатые триггеры обозначаются сдвоенной буквой ТТ.
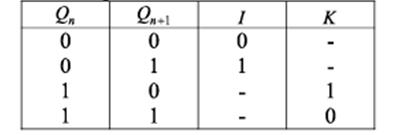
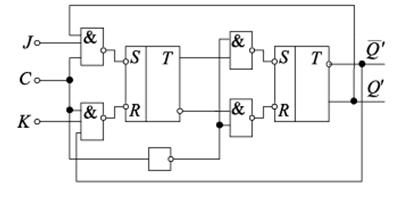
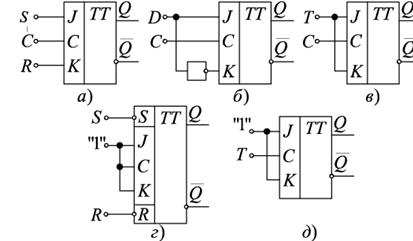
9. JK -триггеры. Назначение, обозначение, принцип действия
« J K-триггер наиболее универсальный триггер, на его основе мо гут быть выполнены другие триггеры. В отличие от R S- триггера, JK- триггер не имеет запрещенных комбинаций входных сигналов.
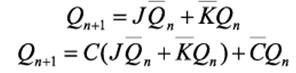
10. Регистры. Назначение, классификация, обозначение, принцип действия
Регистром называется последовательностное устройство, предназначенное для записи, хранения и (или) сдвига информации, представленной в виде многоразрядного двоичного кода. Они содержат несколько D-триггеров, соединенных между собой.
На схемах регистры обозначаются буквами RG. В отечественных сериях микросхем регистрам соответствуют буквы ИР.
По способу приема информации регистры подразделяют на:
- параллельные (статические) – информация записывается и считывается только в параллельной форме;
- последовательные (сдвигающие) – информация записывается и считывается только в последовательной форме;
- последовательно-параллельные – информация записывается или считывается как в параллельной, так и в последовательной формах.
Регистры, срабатывающие по фронту управляющего сигнала С называются тактируемыми.
Регистры, срабатывающие по уровню управляющего сигнала С называются стробируемыми.
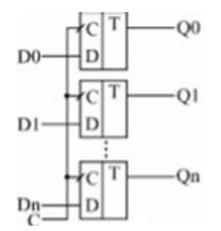
В параллельных регистрах каждый из триггеров имеет свой независимый информационный вход (D) и свой независимый информационный выход. Тактовые входы (С) всех триггеров соединены между собой.
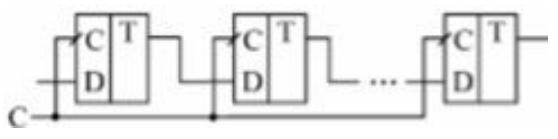
В сдвиговых регистрах все триггеры соединены в последовательную цепочку (выход каждого предыдущего триггера соединен со входом D следующего триггера). Тактовые входы всех триггеров (С) объединены между собой. Входной сигнал последовательно перезаписывается из триггера в триггер по фронту тактового сигнала С.
11.Счетчики. Назначение, классификация, обозначение, принцип действия
Счетчиком называется последовательное устройство, предназначенное для счета входных импульсов и фиксации их числа в двоичном коде.
Счетчики так же, как и сдвиговые регистры, строятся на основе триггеров и комбинационных схем, предназначенной для формирования сигналов управления триггерами.
Счетчики выполняют следующие микооперации:
1) установка в исходное состояние (запись нулевого кода); 2) запись входной информации в параллельной форме;
3) хранение информации;
4) выдача хранимой информации в параллельной форме;
5) инкремент - увеличение хранящегося кодового слова на единицу;
6) декремент - уменьшение хранящегося кодового слова на единицу.
Основные параметры счетчиков:
Модуль счета М - максимальное число импульсов, после прихода которого счетчик устанавливается в исходное состояние.
Время установления выходного кода tK - временной интервал между моментом подачи входного сигнала и моментом установления нового кода на выходе.
Классификация:
По значению модуля счета:
двоичные - модуль счета равен целой степени числа 2 (М = 2n);
двоично-кодированные - модуль счета принимает любое, не равное целой степени числа 2, значение.
По направлению счета:
суммирующие, выполняющие микрооперацию инкремента над хранящимся кодовым словом;
вычитающие, выполняющие микрооперацию декремента над хранящимся кодовым словом;
реверсивные, выполняющие в зависимости от значения управляющего сигнала над хранящимся кодовым словом либо микрооперацию декремента, либо инкремента.
По способу организации межразрядных связей:
счетчики с последовательным переносом - переключение триггеров осуществляется последовательно один за другим;
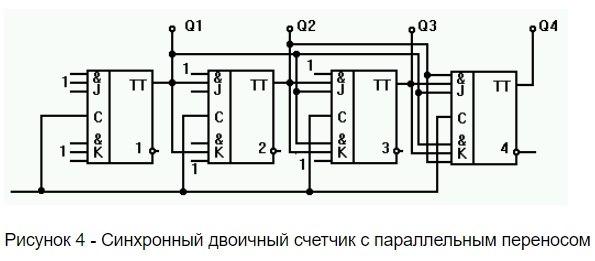
счетчики с параллельным переносом переключение всех триггеров осуществляется одновременно по сигналу синхронизации;
счетчики с комбинированным последовательно-параллельным переносом
12. Построить схему асинхронного триггера с использованием комбинационных логических устройств.
Асинхронный RS -триггер – элемент памяти, который реализован на элементах И—НЕ или ИЛИ—НЕ, снабжен только двумя информационными входами: входом сброса R и входом установки S.
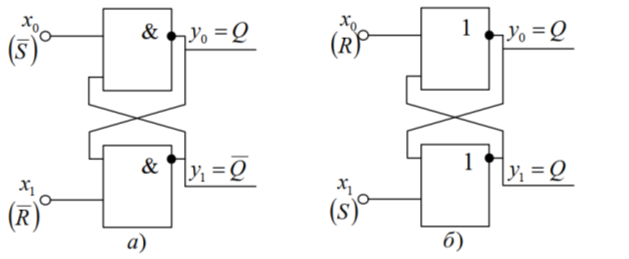
a) Асинхронный триггер на логических элементах И-НЕ
б) Асинхронный триггер на логических элементах ИЛИ-НЕ
13. Построить схему синхронного триггера с использованием комбинационных логических устройств
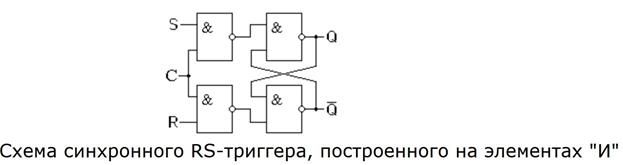
14. Построить схему триггера с использованием комбинационных логических устройств
Схема D - триггера, построенного на логических элементах
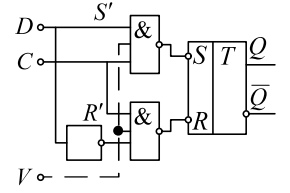
15.Построить схему формирователя временного интервала на основе D -триггера
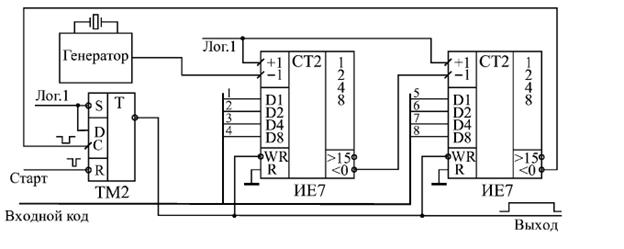
16.Построить схему формирователя короткого импульса на основе D -триггера
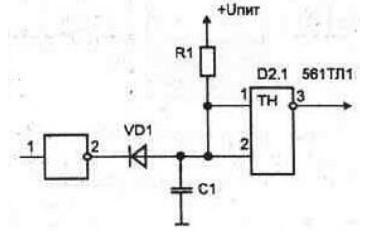
17.Построить схему четырехразрядного параллельного регистра на основе D -триггеров.
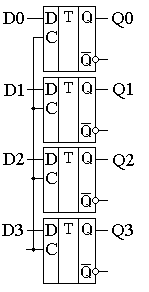
18. Построить схему четырехразрядного сдвигового регистра на основе D - триггеров
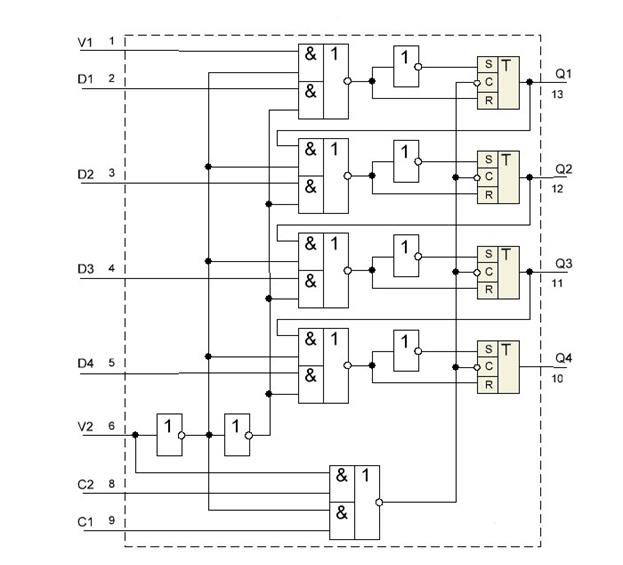
19. Построить формирователь импульсов с длительностью, заданной управляющим кодом
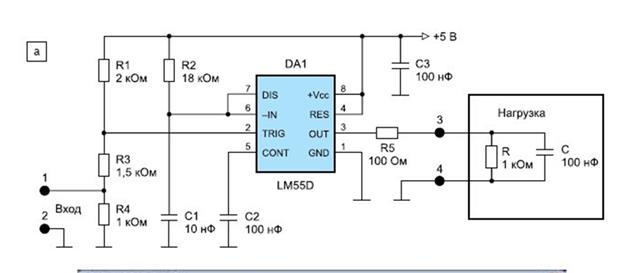
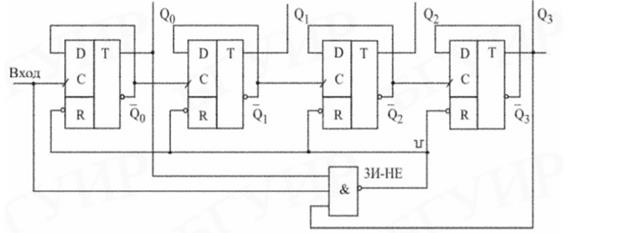
20.Построить схему двоичного счетчика с последовательным переносом.
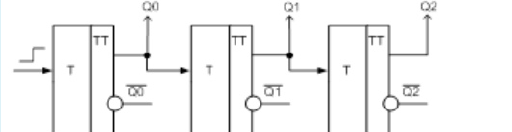
21. Построить схему двоичного счетчика с параллельным переносом
22. Построить схему счетчика с модулем счета десять на основе метода управляемого сброса