Тема 8. Моделі розподіленого лагу

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Питання 1

100 Що таке лаг?
  1-Це функція, що характеризує тісноту зв’язку кожного елемента вектора yt з елементами вектора xt , зсунутим один відносно одного на часовий період τ;
  2-це зрушення, якому відповідає найбільший коефіцієнт взаємної кореляції;
  3-це явище, результатом дії якого ефект від впливу деякого фактора на показник, який характеризує процес, виявляється не одразу, а поступово, через деякий період часу;
  4-це існування взаємозв’язку між послідовними елементами часового чи просторового ряду данних;
  5-це явище, коли дисперсія залишків змінюється для кожного спостереження.

Питання 2

100 Економетрична модель розподіленого лагу визначається так :
  1-Yt = Σaτxt-τ + Σbszt,s + ut;
  2-Yt = Σajxt + ut;
  3-Yt = Σaτxt+τ + ut;
  4-Yt = Σaτxt-τ + ut;
  5-Yt = Σaτxt + ut-τ;

Питання 3

100 Узагальнена економетрична модель розподіленого лагу записується у вигляді :
100 1-Yt = Σaτxt-τ + Σbszt,s + ut;
  2-Yt = Σaτxt-τ + Σbszt,s ;
  3-Yt = Σaτxt+τ + Σbszt,s + ut;
  4-Yt = Σaτxt-τ + ut;
  5-Yt = Σbszt,s + ut;

Питання 4

100 Які найпростіші гіпотези застосовуються відносно залишків в моделях розподіленого лагу?
  1. Залишки є випадковими величинами і розподіляються нормально;
  1. залишки υt = ρut-1 + εt, |ρ| < 1, εt є N(0;Ơυ²);
  залишки описуються автокореляційною функцією першого порядку ut = ρut-1 + εt;
  залишки описуються автокореляційною функцією другого порядку ut = ρut-1 + ρ2ut-2+ υt;
  1. залишки є випадковими величинами і розподіляються нормально; 2. залишки виражені через параметр λ, υt = ut – λut-1, 0≤λ ≤1, де υt є N(0;Ơυ²) ut = ρut-1 + εt, |ρ| < 1, εt є N(0;Ơυ²)
  1. залишки υt = ρut-1 + εt, |ρ| < 1, εt є N(0;Ơυ²);
   

Питання 5

100 Метод інструментальних змінних для оцінки параметрів моделі застосовують тоді, коли :
  1-залишки описуються автокореляційною функцією першого порядку ut = ρut-1 + εt;
  2-залишки не автокорельовані, але існує залежність пояснювальних змінних із залишками;
  3-залишки є випадковими величинами і розподіляються нормально;
  4-залишки описуються автокореляційною функцією другого порядку ut = ρut-1 + ρ2ut-2+ υt;
  5-Залишки незалежні.

Питання 6

100 В заємн а кореляційн а функці я в изначається за формулою:
  1- ;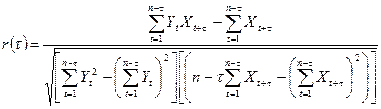
  2- ;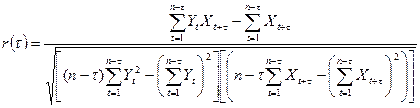
  3- ;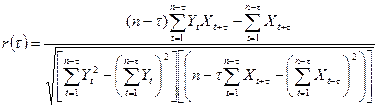
  4- .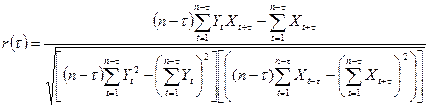

Питання 7

100 Якщо залишки є випадковими величинами і розподіляються нормально, тоді для оцінки параметрів моделі можна застосувати:
100 1-метод найменших квадратів;
  2-метод Ейткена;
  3-ітеративний метод;
  4-метод інструментальних змінних;
  5- алгоритм Уолліса.

Питання 8

100 Якщо залишки описуються авторегресійноюсхемою першого порядку, тоді для оцінки параметрів моделі можна застосувати:
  1-метод найменших квадратів;
  2-метод Ейткена;
  3-ітеративний метод;
  4-метод інструментальних змінних;
  5- алгоритм Уолліса.

Питання 9

100 Якщо залишки для моделі розподіленого лагу подаються у ви вигляді 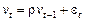, , 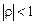тоді для оцінювання параметрів моделі застосовується :
  1-метод найменших квадратів;
  2-метод Ейткена;
  3-ітеративний метод;
  4-метод інструментальних змінних;
  5- всі перераховані алгоритми.

Питання 10

100 Значення взаємної кореляційної функції r (τ) належить множині :
  1-]-1, 0 [ ;
  2- ]-1, 1[ ;
  3-] 0 , 1[ ;
  4-]-1, ∞[ .