Тема 4. Мультиколінеарність
Питання 1
| 100 | Основні наслідки мультиколінеарності : |
| 1-спостерігається високий ступінь кореляції між залишками та незалежною змінною ; | |
| 2-проблеми із статистичними висновками; | |
| 100 | 3-дисперсії оцінок параметрів моделі різко збільшуються, похибки параметрів значно збільшуються , оцінки параметрів можуть бути статистично незначущими; |
| 4-дисперсія залишків змінюється для кожного спостереження або групи спостережень ; | |
| 5-дисперсія залишків постійна. |
Питання 2
| 100 | Мультиколінеарність наявна, коли: |
| 1-ми будуємо неправильну версію істинної моделі ; | |
| 2-незалежна змінна виміряна з помилкою; | |
| 3-дві чи більше незалежних змінних мають високу кореляцію; | |
| 4-дисперсія залишків змінюється для кожного спостереження або групи спостережень ; | |
| 5-дисперсія залишків постійна. |
Питання 3
| 100 | Які статистичні критерії досліджують наявність мультиколінеарності? |
| 1-T- критерій Стьюдента; | |
| 2-всі досліджують ; | |
| 3-χ² -критерій ; | |
| 4-жоден не досліджує ; | |
| 5-F – критерій Фішера. |
Питання 4
| 100 | Який статистичний критерій перевіряє мультиколінеарність усього масиву незалежних змінних: |
| 1-T- критерій Стьюдента; | |
| 2-всі досліджують ; | |
| 3-χ² -критерій ; | |
| 4-жоден не досліджує ; | |
| 5-F – критерій Фішера. |
Питання 5
| 100 | Який статистичний критерій перевіряє парну мультиколінеарність незалежних змінних: |
| 1-T- критерій Стьюдента; | |
| 2-всі досліджують ; | |
| 3-χ² -критерій ; | |
| 4-жоден не досліджує ; | |
| 5-F – критерій Фішера. |
Питання 6
| 100 | Серед наведених статистичних критеріїв знайдіть ті, що застосовуються для оцінювання мультиколінеарності: |
1-λ2=-[n-1- 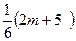 ]ln|r|; ]ln|r|;
| |
2-T= 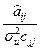 ; ;
| |
3-F= 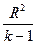 : : 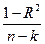 ; ;
| |
4-T= 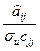 ; ;
| |
5-Fkk=(ckk- 1) 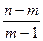 . .
|
Питання 7
| 100 | Якщо детермінант кореляційної матриці прямує до 0, тоді: |
| 1-існує повна мультиколінеарність; | |
| 2-мультиколінеарність відсутня; | |
| 3-потрібно продовжити дослідження; | |
| 4-ніяких висновків стосовно мультиколінеарності зробити неможна; |
Питання 8
| 100 | Якщо детермінант кореляційної матриці прямує до 1, тоді: |
| 1-існує повна мультиколінеарність; | |
| 2-мультиколінеарність відсутня; | |
| 3-потрібно продовжити дослідження; | |
| 4-ніяких висновків стосовно мультиколінеарності зробити неможна; |
Питання 9
| 100 | Коефіцієнт детермінації для кожної змінної можна обчислити за формулою: |
1-R2k=1 - 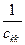 ; ;
| |
2-R2k=1 - 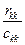 ; ;
| |
3-R2k=1 + 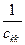 ; ;
| |
4-R2k=1 - 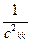 ; ;
| |
| 5-R2k= 1 –ckk. |
Питання 10
| 100 | Частинний коефіцієнт кореляції можна розрахувати за формулою: |
1- 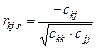 ; ;
| |
2- 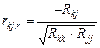 ; ;
| |
3- 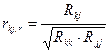 ; ;
| |
4- 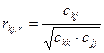 . .
|
Питання 11
| 100 | Для виправлення проблеми мультиколінеарності можна: |
| 1-відкинути одну чи більше незалежних змінних; | |
| 2-використати узагальнений метод найменших квадратів; | |
| 3-використати метод найменших квадратів; | |
| 4-перетворити певним чином незалежні змінні. |








