Тема 3. Економетричне моделювання на основі лінійної регресії
Питання 1
| 100 | Етапи побудови економетричної моделі : |
| 1-постановка задачі, формування вхідної інформації, оцінка параметрів моделі, аналіз залишків, верифікація моделі; | |
| 2-постановка задачі, специфікація моделі, формування вхідної інформації, оцінка параметрів моделі, верифікація моделі; | |
| 3-постановка задачі, специфікація моделі, формування вхідної інформації, оцінка параметрів моделі, аналіз залишків; | |
| 4-постановка задачі, специфікація моделі, формування вхідної інформації, оцінка параметрів моделі, аналіз залишків, верифікація моделі; |
Питання 2
| 100 | Передумови застосування методу найменших квадратів: |
| 1-математичне сподівання залишків дорівнює нулю, значення вектора залишків залежні між собою і мають постійну дисперсію; | |
| 2-математичне сподівання залишків дорівнює нулю, значення вектора залишків незалежні між собою і мають нульову дисперсію; | |
| 3-математичне сподівання залишків не дорівнює нулю, значення вектора залишків незалежні між собою і мають постійну дисперсію; | |
| 4-математичне сподівання залишків дорівнює нулю, значення вектора залишків залежні між собою і не мають постійну дисперсію; | |
| 5-математичне сподівання залишків дорівнює нулю, значення вектора залишків незалежні між собою і мають постійну дисперсію. |
Питання 3
| 100 | Для опису одного економічного процесу прийнятні дві моделі. Обидві адекватні за F - критерієм Фішера. Якій надати перевагу, тій у якої: |
| 1-більше значення F-критерія ; | |
| 2-більшій коефіцієнт детермінації ; | |
| 3-менший коефіцієнт детермінації; | |
| 4-якщо зв'язок нелінійний . |
Питання 4
| 100 | Як обчислити дисперсії залишків, якщо u – залишки, n – число одиниць сукупності, m – число ознак, які описують кожну одиницю ? |
| 1-Ơu2=∑u2/(n-m-1); | |
| 2-Ơu2=∑u2/n; | |
| 3-Ơu2=∑u2/(n-m-2); | |
| 4-Ơu2=∑u2/(n-m)2; | |
| 5-Ơu2=∑u2. |
Питання 5
| 80 | За допомогою економетричної моделі можна побудувати такі види прогнозу: |
| 1- економічний, статистичний; | |
| 2- економічний, математичний; | |
| 3- точковий, інтервальний; | |
| 4- економічний, точковий, інтервальний; | |
| 5- математичний, точковий, статистичний. |
Питання 6
| 100 | У простій лінійній економетричній моделі 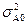  дорівнює: дорівнює:
|
| 1- Ơu2; | |
2- Ơu2/ (∑( 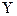 - - 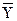 )2; )2;
| |
3- Ơu2 (∑X²)/ (n∑( 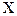 - - 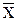 )2); )2);
| |
4- Ơu2/ (∑( 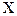 - - 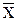 )2; )2;
| |
5- Ơu2/ (n∑( 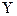 - - 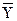 )2). )2).
|
Питання 7
| 100 | У простій лінійній економетричній моделі 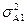  дорівнює: дорівнює:
|
| 1- Ơu2; | |
2- Ơu2/ (∑( 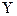 - - 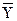 )2; )2;
| |
3- Ơu2 (∑X²)/ (n∑( 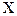 - - 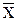 )2); )2);
| |
4- Ơu2/ (∑( 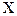 - - 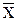 )2; )2;
| |
5- Ơu2/ (n∑( 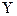 - - 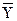 )2). )2).
|
Питання 8
| 100 | Для економетричної моделі з n спостережень інтервал довіри для параметра а 1 рівня значущості α буде дорівнювати: |
1-A0±t(α,n-2) 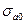 ; ;
| |
2- A1±t(α,n-2) 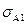 ; ;
| |
3- A 1 ±t(α,n-2) 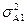 ; ;
| |
4-A1±t(α,n) 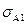 ; ;
| |
5- A 0 ±t(α,n) 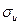 . .
|
Питання 9
| 100 | Для економетричної моделі з n спостережень інтервал довіри для параметра а 0 рівня значущості α буде дорівнювати: |
1-A0±t(α,n-2) 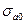 ; ;
| |
2-A1±t(α,n-2) 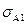 ; ;
| |
3-A 1 ±t(α,n-2) 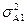 ; ;
| |
4-A1±t(α,n) 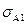 ; ;
| |
5-A 0 ±t(α,n) 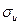 . .
|
Питання 10
| 100 | Перевірку гіпотези про адекватність економетричної моделі можна виконати за F - критерієм: |
1-Fk-1,n-k= 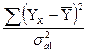 ; ;
| |
2-Fk-1,n-k= 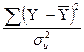 ; ;
| |
3-Fk-1,n-k= 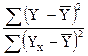 ; ;
| |
4-Fk-1,n-k= 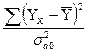
| |
5-Fk-1,n-k= 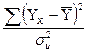 . .
|
Питання 11
| 100 | Для економетричної моделі з n спостережень та k параметрів зв’язок між R ² та F : |
1-Fk,n-k= 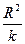 : : 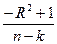 ; ;
| |
2-Fk-1,n-k= 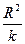 : : 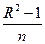 ; ;
| |
3-Fk-1,n-k= 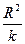 : : 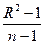 ; ;
| |
4-Fk,n-k= 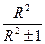 . .
| |
5-Fk-1,n-k= 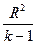 : : 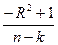 . .
|
Питання 12
| 100 | При перевірці значимості параметра моделі використовуємо : |
| 1-T – тест ; | |
| 2-F- тест ; | |
| 3-χ²- тест; | |
| 4-біноміальний розподіл; | |
| 5-будь-що із згаданого. |
Питання 13
| 100 | Ступені вільності для t - статистики для перевірки значимості параметрів моделі, що складається з 35 спостережень та 4 незалежних змінних, такі: |
| 31 ; | |
| 4; | |
| 32; | |
| 35; | |
| 30. |
Питання 14
| 100 | У простій лінійній економетричній моделі завжди має бути: |
| R >0; | |
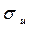 > 0 ; > 0 ;
| |
| А0 > 0 | |
| А0< 0; | |
| R < 0. |








