«санкт-петербургский государственный университет
Министерство науки и высшего образования Российской Федерации
федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И ДИЗАЙНА»
ВЫСШАЯ ШКОЛА ТЕХНОЛОГИИ И ЭНЕРГЕТИКИ
Институт заочного и вечернего обучения
Кафедра промышленной теплоэнергетики
Контрольная работа
по дисциплине
Техническая термодинамика
Вариант №4
| Выполнил | студент группы №7-428, шифр 214-367 Хрептугова Александра Максимовна |
| (фамилия, имя, отчество) | |
| Проверил | доцент, Калиничев Алексей Евгеньевич |
| (должность, фамилия, имя, отчество) | |
|
| |
Санкт-Петербург
2023
Задача 23
Для измерения уровня жидкости в сосуде иногда используется устройство, схема которого изображена на рис.5.
Определить уровень бензина в баке, если 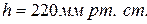 , а его плотность
, а его плотность 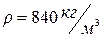 .
.
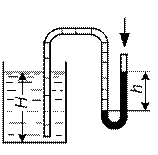
Рисунок 5
Решение:
Полное (абсолютное) давление со стороны бензина:
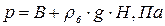 (1)
(1)
где 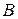 - атмосферное давление,
- атмосферное давление, 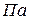 ;
;
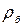 - удельная плотность бензина,
- удельная плотность бензина, 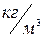 ;
;
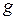 - ускорение свободного падения,
- ускорение свободного падения, 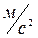 ;
;
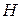 - уровень бензина в сосуде,
- уровень бензина в сосуде, 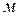 ;
;
Полное (абсолютное) давление со стороны ртути:
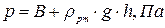 (2)
(2)
где 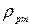 - удельная плотность ртути,
- удельная плотность ртути, 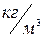 ;
;
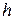 - уровень ртути в трубке,
- уровень ртути в трубке, 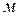 ;
;
Приравнивая правые части уравнений (1) и (2), получаем выражение для определения уровня бензина в сосуде:
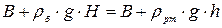 (3)
(3)
откуда получаем
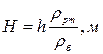 (4)
(4)
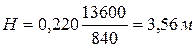
Ответ: 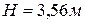 .
.
Задача 40
Дымовые газы, образовавшиеся в топке парового котла, охлаждаются с 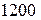 до
до 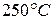 .
.
Во сколько раз уменьшается их объем, если давление газов в начале и в конце газоходов одинаково?
Решение:
Пользуясь характеристическим уравнением для двух различных состояний какого-либо газа, можно получить выражение для определения любого параметра при переходе от одного состояния к другому, если значения остальных параметров известны:
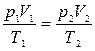 (1)
(1)
где 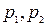 - начальное и конечно давление газа,
- начальное и конечно давление газа, 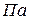 ;
;
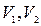 - начальный и конечный объем газа,
- начальный и конечный объем газа, 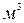 ;
;
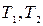 - начальная и конечная температура газа,
- начальная и конечная температура газа,  ;
;
учитывая, что давление в процессе остается неизменным, можно переписать формулу (1) следующим образом
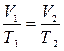 (2)
(2)
отсюда находим что объем дымовых газов уменьшается в
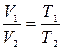 (3)
(3)
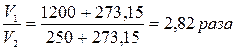
Ответ: в 2,82 раза.
Задача 57
Какой объем займет 1 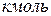 газа при
газа при 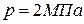 и
и 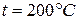 ?
?
Решение:
Объем занимаемый 1  газа определяем из уравнения состояния идеального газа:
газа определяем из уравнения состояния идеального газа:
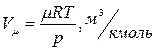 (1)
(1)
где 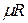 - универсальная газовая постоянная 1
- универсальная газовая постоянная 1  газа,
газа, 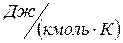 ;
;
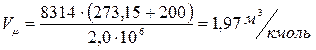
Ответ: 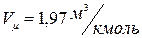 .
.
Задача 67
Определить подъемную силу воздушного шара, наполненного водородом, если объем его на поверхности земли равен 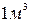 при давлении
при давлении 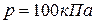 и температуре
и температуре 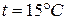 .
.
Решение:
На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (веса) воздуха и водорода в объеме шара:
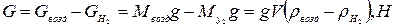 (1)
(1)
где 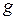 - ускорение свободного падения,
- ускорение свободного падения, 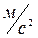 .
.
Значения плотностей газов определяем из уравнения состояния:
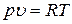 (2)
(2)
где 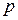 - абсолютное давление газа,
- абсолютное давление газа, 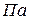 ;
;
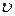 - удельный объем газа,
- удельный объем газа, 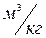 ;
;
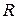 - газовая постоянная газа,
- газовая постоянная газа, 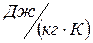 ;
;
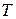 - температура газа,
- температура газа, 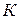 ;
;
отсюда находим плотность газа
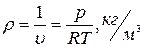 (3)
(3)
- плотность воздуха
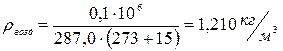
- плотность водорода
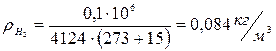
Следовательно, подъемная сила шара по формуле (1) равна:
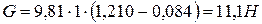
Ответ: 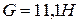 .
.
Задача 92
Газовая смесь имеет следующий массовый состав: СО2=12%; О2=8% и N2=80%.
До какого давления нужно сжать эту смесь, находящуюся при нормальных условиях, чтобы плотность ее составляла 1,6 кг/м³?
Решение:
Газовая постоянная смеси:
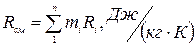 (1)
(1)
где 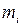 - массовая доля
- массовая доля 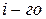 компонента смеси;
компонента смеси;
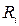 - газовая постоянная
- газовая постоянная 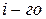 газа смеси,
газа смеси, 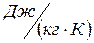 ;
;
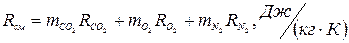 (2)
(2)
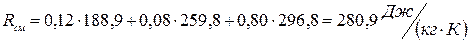
Давление определяем из уравнения состояния идеального газа:
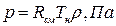 (3)
(3)
где 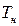 - температура при нормальных условиях (справочная величина),
- температура при нормальных условиях (справочная величина), 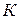 ;
;
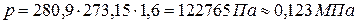
Ответ: р=0,123 МПа.
Задача 116
Продукты сгорания топлива поступают в газоход парового котла при температуре газов tʹг=1100 ºС и покидают газоход при температуре tʺг=700 ºС. Состав газов по объему: 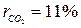 ;
; 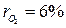 ;
; 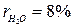 ;
; 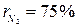 .
.
Определить, какое количество теплоты теряет 1 м³ газовой смеси, взятой при нормальных условиях.
Решение:
Количество теплоты, которое теряет 1 м³ газовой смеси, взятой при нормальных условиях:
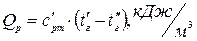 (1)
(1)
где 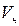 - объем смеси при нормальных условиях,
- объем смеси при нормальных условиях, 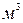 ;
;
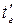 и
и 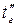 - начальная и конечная температуры газовой смеси,
- начальная и конечная температуры газовой смеси, 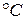 ;
;
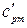 - объемная теплоемкость газовой смеси при нормальных условиях,
- объемная теплоемкость газовой смеси при нормальных условиях, 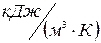 .
.
Объемные теплоемкости газовой смеси при нормальных условиях:
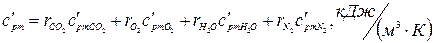 (2)
(2)
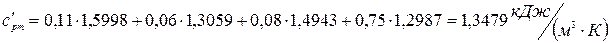 тогда
тогда
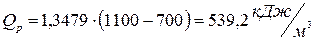
Ответ: Qp=539,2 кДж/м³.
Задача 120
Мощность турбогенератора 12000 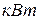 . к. п. д. генератора 0,97. Какое количество воздуха нужно пропустить через генератор для его охлаждения, если конечная температура воздуха не должна превышать
. к. п. д. генератора 0,97. Какое количество воздуха нужно пропустить через генератор для его охлаждения, если конечная температура воздуха не должна превышать 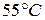 ?
?
Температура в машинном отделении равна 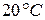 ; среднюю теплоемкость воздуха
; среднюю теплоемкость воздуха 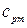 принять равной 1,0
принять равной 1,0 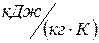 .
.
Решение:
Количество теплоты, выделяемое турбогенератором при работе:
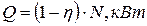 (1)
(1)
где 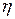 - коэффициент полезного действия (к. п. д) генератора;
- коэффициент полезного действия (к. п. д) генератора;
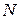 - мощность генератора,
- мощность генератора, 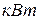 .
.
Количество теплоты, необходимое для охлаждения генератора:
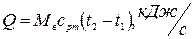 (2)
(2)
где 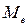 - расход воздуха,
- расход воздуха, 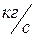 ;
;
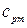 - средняя теплоемкость воздуха,
- средняя теплоемкость воздуха, 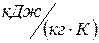 ;
;
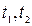 - начальная и конечная температуры воздуха,
- начальная и конечная температуры воздуха, 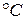 .
.
Приравнивая правые части выражений (1) и (2), получаем
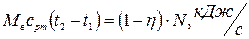 (3)
(3)
откуда находим искомый расход воздуха через турбогенератор
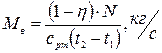 (4)
(4)
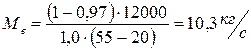
Ответ: 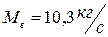 .
.
Задача 131
В котельной электростанции за 10  работы сожжено 100 т каменного угля с теплотой сгорания
работы сожжено 100 т каменного угля с теплотой сгорания 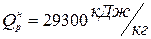 .
.
Найти количество выработанной электроэнергии и среднюю мощность станции, если к.п.д. процесса преобразования тепловой энергии в электрическую составляет 20%.
Решение:
Количество теплоты, превращенной в электрическую энергию за 10 часов работы:
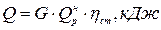 (1)
(1)
где 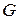 - количество каменного угля сожженного в котельной электростанции за 10 часов работы,
- количество каменного угля сожженного в котельной электростанции за 10 часов работы, 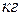 ;
;
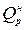 - теплота сгорания топлива,
- теплота сгорания топлива, 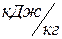 ;
;
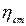 - коэффициент полезного действия;
- коэффициент полезного действия;
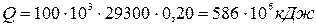
Эквивалентная ей электрическая энергия или работа:
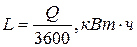 (2)
(2)
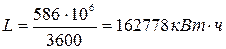
Следовательно, средняя электрическая мощность электрической станции составляет:
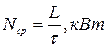 (3)
(3)
где  - время работы котельной,
- время работы котельной,  ;
;
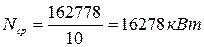
Ответ: 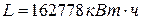 ,
, 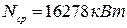 .
.
Задача 137
В машине вследствие плохой смазки происходит нагревание 200  стали на
стали на 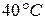 в течение
в течение 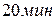 .
.
Определить вызванную этим потерю мощности машины. Теплоемкость стали принять равной 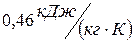 .
.
Решение:
Потеря мощность машины равна количеству теплоты, выделившейся в течение 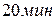 , то есть:
, то есть:
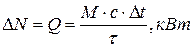 (1)
(1)
где 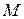 - масса стали,
- масса стали, 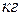 ;
;
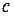 - теплоемкость стали,
- теплоемкость стали, 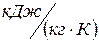 ;
;
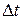 - повышение температуры стали,
- повышение температуры стали, 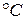 ;
;
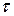 - время,
- время, 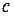
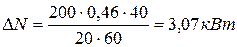
Ответ: 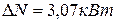 .
.
Задача 236
Определить, является ли политропным процесс сжатия газа, для которого параметры трех точек имеют следующие значения: р1=0,12 МПа; t1=30 ºС; р2=0,36 МПа; t2=91 ºС; р3=0,54 МПа; t3=116 ºС.
Решение:
Любой процесс изменения состояния рабочего тела, происходящий при постоянной теплоемкости, называется политропным. Уравнение этого процесса может быть получено на основании уравнения первого закона термодинамики для идеального газа (в двух формах записи):
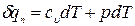 (1)
(1)
или
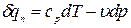 (2)
(2)
Исходя из понятия теплоемкости, в политропном процессе
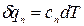 (3)
(3)
где 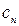 - теплоемкость политропного процесса.
- теплоемкость политропного процесса.
Тогда уравнения первого закона термодинамики для политропного процесса примут вид:
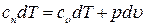 или
или 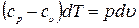 (4)
(4)
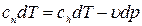 или
или 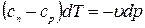 (5)
(5)
Разделив уравнение (4) на уравнение (5), получим
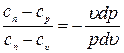 (6)
(6)
Обозначив отношение 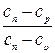 , постоянное для данного процесса, так:
, постоянное для данного процесса, так:
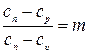 (7)
(7)
Величина 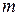 , зависящая от теплоемкости
, зависящая от теплоемкости 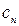 политропного процесса, называется показателем политропы. Будучи постоянным для конкретного процесса, значение показателя политропы может изменяться в зависимости от теплоемкости
политропного процесса, называется показателем политропы. Будучи постоянным для конкретного процесса, значение показателя политропы может изменяться в зависимости от теплоемкости 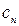 от
от 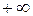 до
до 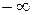 и определяет характер процесса.
и определяет характер процесса.
Рассчитаем показатели политропы по формуле:
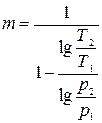 (8)
(8)
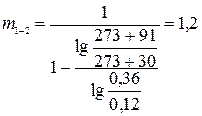
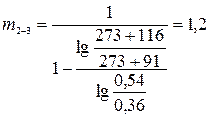
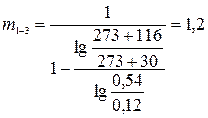
Так как 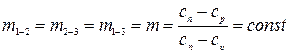 , то процесс является политропным.
, то процесс является политропным.
Ответ: процесс – политропный, m=1,2.
Задача 296
Производительность компрессора 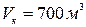 воздуха в час; начальные параметры воздуха:
воздуха в час; начальные параметры воздуха: 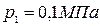 ;
; 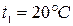 ; конечное давление
; конечное давление 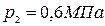 .
.
Определить теоретическую мощность двигателя для привода компрессора, если сжатие будет производиться изотермически. На сколько возрастет теоретическая мощность двигателя, если сжатие в компрессоре будет совершаться по адиабате?
Решение:
Работа компрессора при изотермическом сжатии:
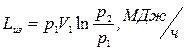 (1)
(1)
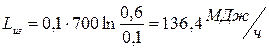
Теоретическая мощность двигателя для привода компрессора:
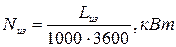 (2)
(2)
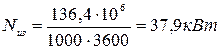
Работа компрессора при адиабатном сжатии:
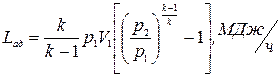 (3)
(3)
где 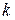 - показатель адиабаты воздуха;
- показатель адиабаты воздуха;
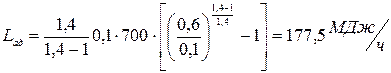
Теоретическая мощность двигателя для привода компрессора:
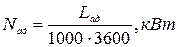 (4)
(4)
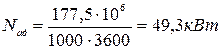
При переходе с изотермического на адиабатное сжатие теоретическая мощность двигателя на привод компрессора увеличивается на:
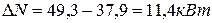
Ответ: 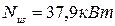 ,
, 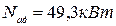 .
.
Задача 349
Для регулирования температуры перегретого пара в некоторых случаях к нему примешивают насыщенный пар. Определить, какое количество насыщенного пара при давлении 4 МПа над прибавить к 1 кг перегретого пара при 3,9 МПа и 470 ℃ для снижения температуры пара до 450 ℃ при неизменном давлении.
Решение:
Составим материальный баланс пара

где mнп – масса насыщенного пара при р = 4 МПа, кг;
mпп1 – масса перегретого пара при р = 3,9 МПа и t = 470 ℃, кг;
mпп2 – масса перегретого пара при р = 3,9 МПа и t = 450 ℃, кг.
В уравнении (1) две неизвестных величины. Для решения задачи необходимо еще одно уравнение – уравнение энергетического баланса.
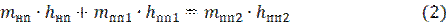
где hнп – энтальпия насыщенного пара при р = 4 МПа, кДж/кг;
hпп1 – энтальпия перегретого пара при р = 3,9 МПа и t = 470 ℃, кг;
hпп2 – энтальпия перегретого пара при р = 3,9 МПа и t = 450 ℃, кг;
Подставим параметры из (1) в уравнение энергетического баланса
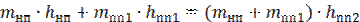
Группируем подобные
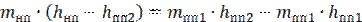
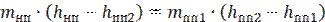
Выражаем количество насыщенного пара
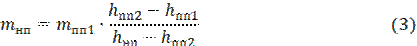
Для определения значения энтальпий, входящих в (3), воспользуемся таблицами воды и водяного пара в состоянии насыщения и перегрева.
Энтальпия насыщенного пара при 4,0 МПа
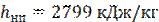
Энтальпия перегретого пара при 3,9 МПа и 470 ℃
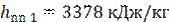
Энтальпия перегретого пара при 3,9 МПа и 450 ℃
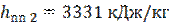
Подставим найденные значения в (3), учитывая, что по условию задачи mпп = 1 кг.
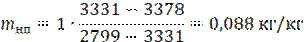
Ответ: m = 0,088 кг/кг.
Задача 369
Из парового котла поступает в пароперегреватель 2700 кг/ч пара при р=1,6 МПа и х=0,98. Температура пара после пароперегревателя равна 400 ºС.
Найти количество теплоты, которое пар получает в пароперегревателе, и отношение диаметром паропроводов до и после пароперегревателя, считая скорости пара в них одинаковыми.
Решение:
По таблице теплофизических свойств насыщенного водяного пара (по давлениям) при 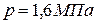 находим:
находим: 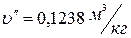 ,
, 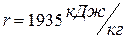 ,
, 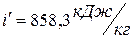 .
.
По таблице свойств перегретого пара при давлении 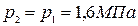 (так как процесс изобарный) и температуре
(так как процесс изобарный) и температуре 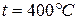 находим:
находим: 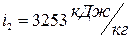 ,
, 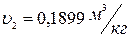 .
.
Количество теплоты, которое пар получает в пароперегревателе:
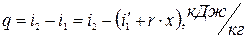 (1)
(1)
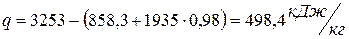
Общее количество теплоты:
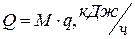 (2)
(2)
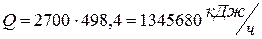
Удельный объем пара до пароперегревателя:
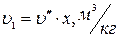 (3)
(3)
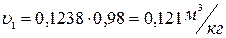
Обозначая сечения трубопровода до и после пароперегревателя соответственно через  и
и 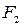 и скорость протекания пара в них через
и скорость протекания пара в них через 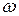 , получаем:
, получаем:
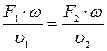 (4)
(4)
или
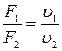 (5)
(5)
учитывая, что 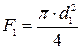 ,
, 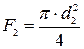 и подставляя эти выражения в выражение (5), получаем
и подставляя эти выражения в выражение (5), получаем
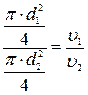 (6)
(6)
после сокращений
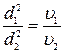 (7)
(7)
откуда
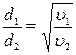 (8)
(8)
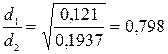
Ответ: Q=1345680 кДж/x, d1/d2=0,798.
Задача 388
5 кг водяного пара, параметры которого р1=2 МПа и V1=0,5 м³, расширяются адиабатно до давления р2=0,2 МПа.
Определить конечный объем пара, степень сухости его и произведенную им работу.
Решение:
Начальный удельный объем пара:
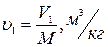 (1)
(1)
где 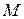 - масса пара,
- масса пара, 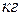 ;
;
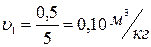
По 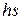 - диаграмме водяного пара на пересечении изобары
- диаграмме водяного пара на пересечении изобары 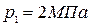 и изохоры
и изохоры 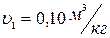 находим точку 1, характеризующую начальное состояние пара. Точка 1 находится в области перегретого пара. Энтальпия в точке 1 составляет
находим точку 1, характеризующую начальное состояние пара. Точка 1 находится в области перегретого пара. Энтальпия в точке 1 составляет 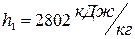 .
.
Адиабатный процесс расширения протекает при постоянном значении энтропии, поэтому точку 2, характеризующую состояние пара после расширения находим на пересечении изоэнтропы 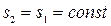 и изобары
и изобары 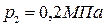 . Точка 2 находится в области влажного пара. Параметры пара в точке 2:
. Точка 2 находится в области влажного пара. Параметры пара в точке 2: 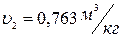 ,
, 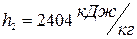 . Степень сухости
. Степень сухости 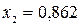 .
.
Конечный объем пара:
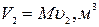 (2)
(2)
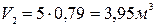
Работа, произведенная паром:
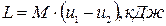 (3)
(3)
где 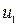 - начальная внутренняя энергия пара,
- начальная внутренняя энергия пара, 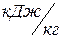 ;
;
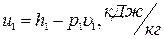 (4)
(4)
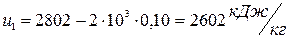
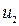 - конечная внутренняя энергия пара,
- конечная внутренняя энергия пара, 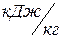 ;
;
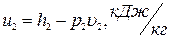 (5)
(5)
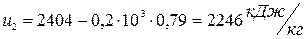
тогда
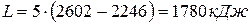
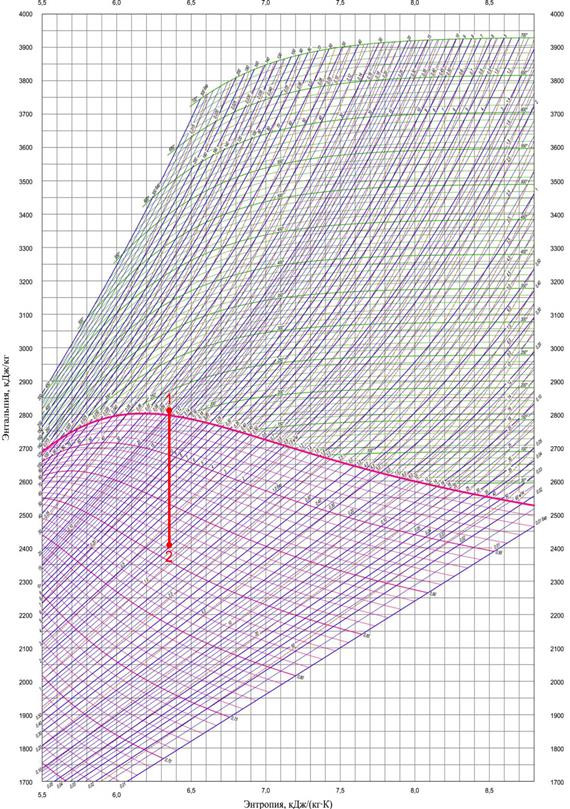
Рисунок 1 – Адиабатный процесс расширения пара в 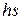 - диаграмме.
- диаграмме.
Ответ: V2=3,95 м³, х2=0,862, L=1780 кДж.
Задача 416
Пар при давлении р1=10 МПа и t1=320 ºС дросселируется до р2=3 МПа.
Определить параметры конечного состояния и изменение температуры пара.
Решение:
По 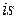 - диаграмме водяного пара находим начальное состояние пара (точка 1) на пересечении изобары
- диаграмме водяного пара находим начальное состояние пара (точка 1) на пересечении изобары 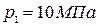 и изотермы
и изотермы 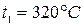 и проводим через полученную точку линию постоянной энтальпии. В пересечении с изобарой
и проводим через полученную точку линию постоянной энтальпии. В пересечении с изобарой 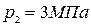 находим точку 2, характеризующую конечное состояние пара. Параметры пара в точке 2:
находим точку 2, характеризующую конечное состояние пара. Параметры пара в точке 2: 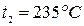 ,
, 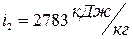 ,
, 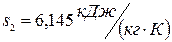 ,
, 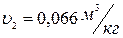 ,
, 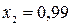 .
.
Изменение температуры пара:
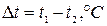 (1)
(1)
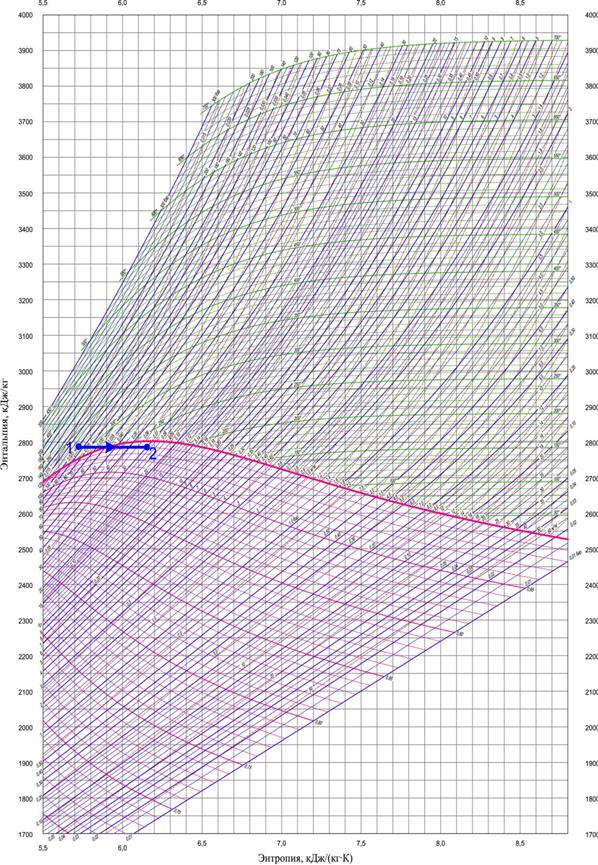 Рисунок 1 - Процесс дросселирования пара в
Рисунок 1 - Процесс дросселирования пара в  - диаграмме.
- диаграмме.
Ответ: х2=0,99, Δt=85 ºC.
Задача 420
По паропроводу течет влажный пар, параметры которого р1 = 1 МПа и х1 = 0,98. Часть пара через дроссельный вентиль перепускается в паропровод, давление в котором р2 = 0,12 МПа.
Определить состояние пара в паропроводе низкого давления.
Решение:
По диаграмме  находим на пересечении изобары
находим на пересечении изобары  и линии постоянной степени сухости
и линии постоянной степени сухости 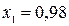 находим точку 1, характеризующую начальное состояние пара и проводим через полученную точку линию постоянной энтальпии (рисунок 1). На пересечении с изобарой
находим точку 1, характеризующую начальное состояние пара и проводим через полученную точку линию постоянной энтальпии (рисунок 1). На пересечении с изобарой 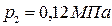 находим точку 2, характеризующую конечное состояние пара. Точка 2 находится в области перегретого пара. Температура, соответствующая этой точке равна
находим точку 2, характеризующую конечное состояние пара. Точка 2 находится в области перегретого пара. Температура, соответствующая этой точке равна 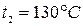 .
.

Рисунок 1 – Процесс дросселирования пара в 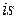 - диаграмме.
- диаграмме.
Ответ: пар перегретый: t2 = 130ºС.
Задача 425
Определить термический к.п.д. и мощность паровой машины, работающей по циклу Ренкина, при следующих условиях: при впуске пар имеет давление 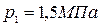 и температуру
и температуру 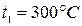 ; давление пара при выпуске
; давление пара при выпуске 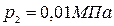 ; часовой расход пара составляет
; часовой расход пара составляет 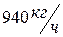 .
.
Решение:
По 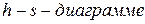 при начальных параметрах
при начальных параметрах 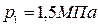 и
и 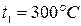 находим
находим 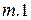 , которая характеризует состояние сухого перегретого пара на входе в турбину. Удельная энтальпия пара в
, которая характеризует состояние сухого перегретого пара на входе в турбину. Удельная энтальпия пара в 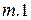 составляет
составляет 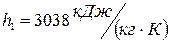 .
.
Опускаясь по адиабате 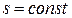 до пересечения с изобарой
до пересечения с изобарой 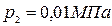 находим
находим 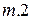 , которая характеризует состояние пара на входе в конденсатор. Энтальпия в
, которая характеризует состояние пара на входе в конденсатор. Энтальпия в 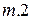 составляет
составляет 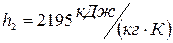 .
.
По таблице насыщенных водяных паров находим энтальпию пара в 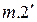 (левая пограничная кривая). При
(левая пограничная кривая). При 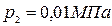 удельная энтальпия составляет
удельная энтальпия составляет 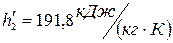 .
.
Термический к.п.д цикла Ренкина:
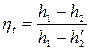 (1)
(1)
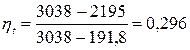
Мощность паровой машины:
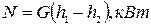 (2)
(2)
где 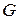 - секундный расход пара,
- секундный расход пара, 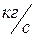 ;
;
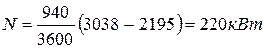
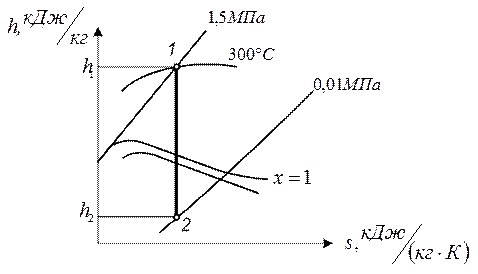
Рисунок 1 - Определение энтальпии пара в процессе цикла Ренкина по диаграмме  .
.
Ответ: 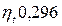 ,
, 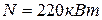 .
.
Задача 434
Турбины высокого давления мощностью N=100000 кВт работают при р1=9 МПа и t1=480 ºС, р2=0,004 МПа. Определить термический к.п.д. цикла Ренкина для данных параметров и достигнутое улучшение термического к.п.д. по сравнению с циклом Ренкина для параметров пара: р1=2,9 МПа, t1=400 ºС; р2=0,004 МПа.
Решение:
Первый вариант: 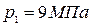 ,
, 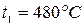 ,
, 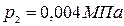 .
.
Значения энтальпий 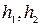 и температуру воды
и температуру воды 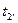 (конденсата) находим по диаграмме
(конденсата) находим по диаграмме 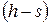 :
: 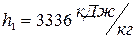 ,
, 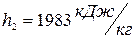 ,
, 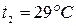 .
.
Работа, получаемая в турбине:
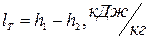 (1)
(1)
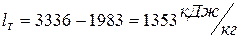
Термический  цикла:
цикла:
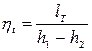 (2)
(2)
где 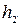 - энтальпия питательной воды:
- энтальпия питательной воды:
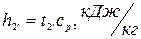 (3)
(3)
тут 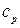 - удельная теплота воды при постоянном давлении,
- удельная теплота воды при постоянном давлении, 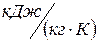 ;
;
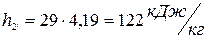
Поставляя полученное значение в формулу (2), находим
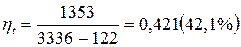
Расход пара:
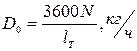 (4)
(4)
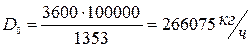
Второй вариант: 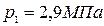 ,
, 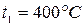 ,
, 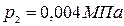 .
.
Значения энтальпий 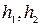 и температуру воды
и температуру воды 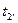 (конденсата) находим по диаграмме
(конденсата) находим по диаграмме 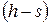 :
: 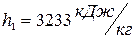 ,
, 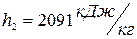 ,
, 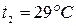 .
.
Работа, получаемая в турбине:
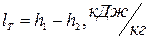 (5)
(5)
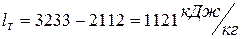
Энтальпию питательной воды определяем по формуле (3)
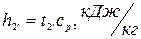 (7)
(7)
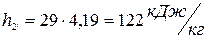
тогда по формуле (2)
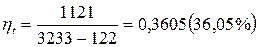
Расход пара:
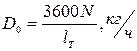 (8)
(8)
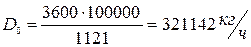
Достигнутое улучшение термического к.п.д. по сравнению с циклом Ренкина:
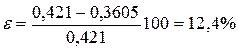
Уменьшение расхода пара составит:
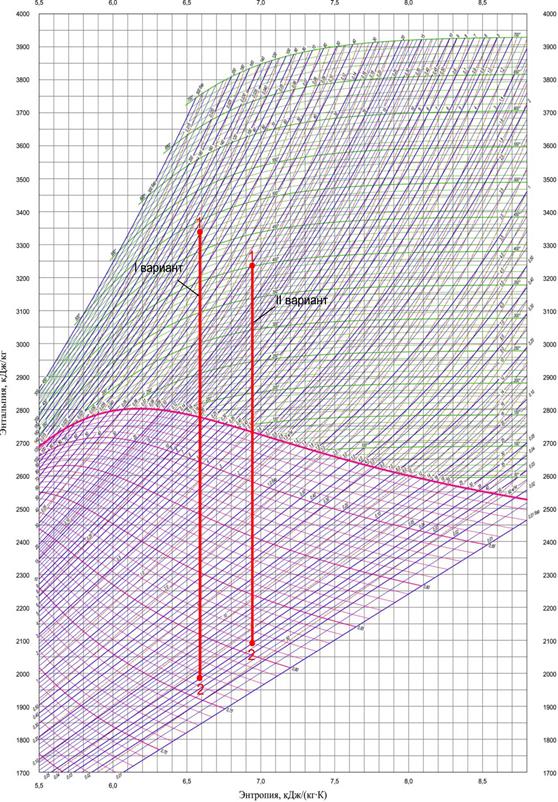
Рисунок 1 - Определение энтальпии пара в процессе цикла Ренкина по диаграмме 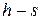 .
.
Ответ: ηt=42,1%, ε=14,4%.
Задача 459
Теоретическая мощность аммиачного компрессора холодильной установки составляет 50 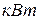 . Температура испарения аммиака
. Температура испарения аммиака 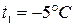 . Из компрессора пар аммиака выходит сухим насыщенным при температуре
. Из компрессора пар аммиака выходит сухим насыщенным при температуре 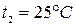 . Температура жидкого аммиака понижается в редукционном вентиле.
. Температура жидкого аммиака понижается в редукционном вентиле.
Определить холодопроизводительность 1 кг аммиака и часовую холодопроизводительность всей установки.
Решение:
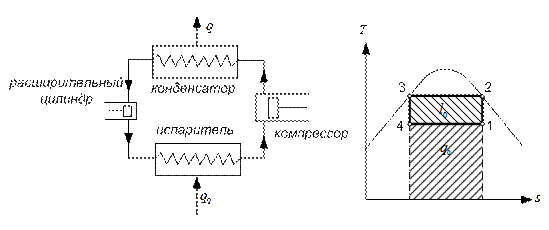
Рисунок 1 - Схема и цикл аммиачной компрессорной холодильной машины
Холодопроизводительность аммиака (количество теплоты, поглощаемой 1 кг аммиака в охлаждаемом помещении):
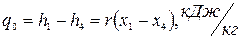 (1)
(1)
По таблице свойств насыщенного пара аммиака при 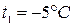 находим
находим 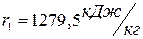 .
.
Значения 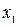 и
и 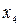 определяем аналитически, используя постоянство энтропии в обратимом адиабатном процессе. Следовательно, в процессе 1-2
определяем аналитически, используя постоянство энтропии в обратимом адиабатном процессе. Следовательно, в процессе 1-2
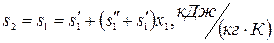 (2)
(2)
По таблице свойств насыщенного пара аммиака находим:
При 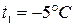 :
: 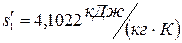 ;
; 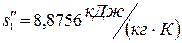 .
.
При 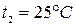
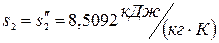 .
.
Тогда
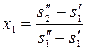 (3)
(3)
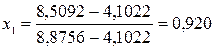
Таким же образом определяем степень сухости влажного насыщенного пара аммиака в точке 4:
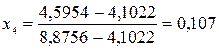
Следовательно,
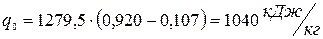
Энтальпия насыщенного пара в точке 1:
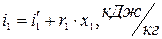 (4)
(4)
где 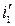 - энтальпия жидкого аммиака при
- энтальпия жидкого аммиака при 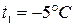 (справочные данные),
(справочные данные), 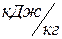 ;
;
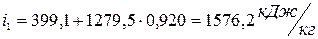
Энтальпию пара, выходящего из компрессора, поскольку он является сухим насыщенным, определяем непосредственно по таблице свойств насыщенного пара аммиака 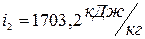 .
.
Удельная работа, затраченная на привод компрессора:
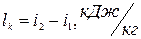 (5)
(5)
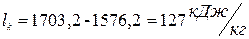
Массовый расход аммиака находим из формулы для определения теоретической мощности компрессора:
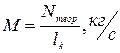 (6)
(6)
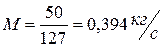
Часовая холодопроизводительность всей установки:
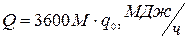 (7)
(7)
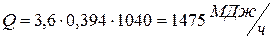
Ответ: 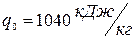 ,
, 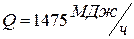 .
.
Задача 464
Аммиачная холодильная установка должна производить 500 кг/ч льда при 0 ℃ из воды, имеющей температуру 20 ℃. Компрессор этой установки всасывает пар аммиака при температуре – 10 ℃ и степени сухости х = 0,98 и сжимает его адиабатно до давления 1 МПа. Из компрессора пар аммиака поступает в конденсатор, конденсируется в нем, причем жидкий аммиак переохлаждается до 15 ℃. После дросселирования аммиак поступает в испаритель, где он испаряется при температуре – 10 ℃ и вновь всасывается компрессором.
Определить часовой расход аммиака, холодопроизводительность установки, количество теплоты, отводимой в конденсаторе охлаждающей водой, степень сухости аммиака в конце дросселирования и теоретическую мощность двигателя для привода компрессора. Представить цикл в диаграмме Ts. Сравнить значение холодильных коэффициентов данного цикла и цикла Карно, осуществляемого в том же интервале температур. Теплоту плавления льда принять равной 331 кДж/кг.
Решение:
Задачу будем решать с помощью диаграммы i - lgP хладагента Аммиак (рис. 1), на которую нанесем реперные точки, согласно заданным начальным и конечным параметрам, а также известным термодинамическим процессам, протекающим в холодильной машине.
Точка 1.
Начальная точки 1, которая расположена в области влажного пара на линии сухости х = 0,98 при температуре – 10 ℃ и давлении 0,3 МПа. Для повышения точности расчетов значение давления р1 и энтропии s1 = s’’ берем из таблицы 2. «Термодинамические параметры насыщенного пара аммиака».
| Температура: t1 = | -10 | ˚C |
| Давление: р1 = | 0.3 | МПа |
| Сухость х = | 0,98 | |
| Энтальпия: h1 = | 1662.6 | кДж/кг |
| Энтропия: s1 = s’’ = | 8.8 | кДж/(кг∙К) |
Точка 1 ’.
Точка 1’ расположена на верхней пограничной кривой при температуре – 10 ℃ и давлении 0,3 МПа. Процесс 1’-1 – изобарный, и одновременно изотермический.
| Температура: t1 = | -10 | ˚C |
| Давление: р1 = | 0,3 | МПа |
| Энтальпия: h1 = | 1669 | кДж/кг |
| Энтропия: s1 = s’’ = | 8.94 | кДж/(кг∙К) |
Точка 2 – сжатие в компрессоре
Процесс 1’-2 адиабатный, происходит при постоянной энтропии. Точка 2 расположена на пересечении линии s2 = s1 – const с линией температуры t2. Значение давления р1 уточняем по данным таблицы 2.
| Давление: р2 = | 1.0 | МПа |
| Температура: t2 = | 25 | ˚C |
| Энтропия: s2 = s1 = | 8,94 | кДж/(кг∙К) |
| Энтальпия: h2 = | 1850 | кДж/кг |
Точка 3 – конденсация.
Процесс 2-3 изобарный. Точка 3 расположена на пересечении линии р2– const с линией температуры t3 = –15 ℃.
| Температура: t3 = | 15 | ˚C |
| Давление: р3 = р2 = | 1,0 | МПа |
| Энтальпия: h3 = | 490 | кДж/кг |
Точка 4
Процесс 3-4 происходит при постоянной энтальпии. Точка 3 расположена на пересечении линии h3 – const с линией давления р1. Значение энтальпии находим проводя вертикальную линию вниз.
| Температура: t4 = t1 = | -10 | ˚C |
| Давление: р4 = р1 = | 0,3 | МПа |
| Энтальпия: h4 = h3 = | 490 | кДж/кг |
Определим количество тепла, которое отбирается от воды при превращении ее в лед.
Теплота, отнимаемая при охлаждении воды от 20 ℃ до 0 ℃
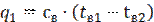
где cв = 4,187 кДж/(кг*К) – изобарная теплоемкость воды;
tв1 = 20 ℃ - начальная температура воды;
tв2 = 0 ℃ - конечная температура воды;
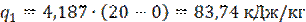
Теплота, отнимаемая при фазовом переходе вода-лед
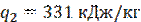
Общее количество теплоты, которое необходимо отнять у воды,
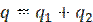
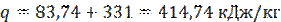
Холодопроизводительность установки
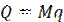
где М = 500 кг/ч – производительность ледогенератора.
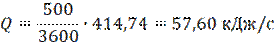
Расход аммиака Ма найдем из уравнения теплового баланса
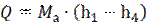
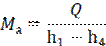
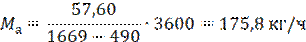
Находим количество теплоты, отводимой в конденсаторе охлаждающей водой.
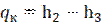
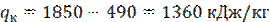
Количество теплоты, отводимой в конденсаторе охлаждающей водой
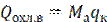
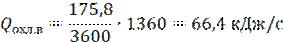
Найдем теоретическую мощность двигателя для привода компрессора.
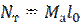
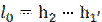
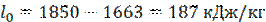

Холодильный коэффициент установки
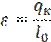
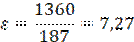
Холодильный коэффициент установки цикла Карно
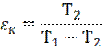
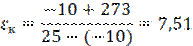
Ответ: Ма = 176 кг/ч; Q = 57,6 кДж/с; Qохл.в. = 66,4 кДж/с; x1 = 9%; Nт = 8,9 кВт; ε = 7,27; εк = 7,51;








